Dynamic order submission and herding behavior in electronic trading

Similar to Engle (2000), the joint conditional density of (X_i,Y_i)_i∈N can be rewritten as

                                   fX_i,Y_i .                           (5)

                                                                            fACD                                         fACL

This concept has been adapted in previous decomposition models to study price movements (e.g., Rydberg and Shephard 2003). In this study, it is assumed that

                                                   p                               q

_i^∗ (6) j=1 k=1

and

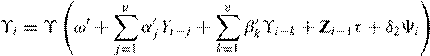                     .               (7)

This bivariate framework reveals not only the relation between the order choice and order duration, but also their joint dynamics. The dependence between X_i and Y_i is captured by both (6) and (7), each of which contains and influences the information for the other process, and both are adapted to F_i−1. The history of the order book is embedded in both components. Economically, this model implies that the market behaves asymmetrically, if 0, indicating a disequilibrium model where the demand and supply side of the book affect the order submission differently (see also Ranaldo 2004). In a perfect market where everyone knows the “true” price, there should be no significant difference in buying or selling an asset. But for δ₁ > 0, traders on the demand side act more frequently and provide more liquidity than the supply side, and vice versa for δ₁ < 0. Similarly, for 0, the ACL model implies an impact of the expected duration on order submission: if δ₂ > 0, bid spells tend to take more time, again signaling higher activity on the opposite market side, and vice versa for δ₂ < 0. In an equilibrium model without asymmetric information, selling a good should be as easy as buying one.

III.  Estimation and Diagnostics

It is well known that financial markets pass through hectic periods of increased activity as well as calm slowdowns. Previous studies find a consistent diurnal pattern oftradingactivitiesoverthecourseofatradingdaybecauseoftheinstitutionalcharacteristics of organized financial markets (like predetermined opening and closing hours or intraday auctions). Because the rate of information arrival also varies over the trading day, it is necessary to take regular daily seasonality into account. Therefore, smoothing techniques are required to obtain deseasonalized observations. Let D_i denote the observed order duration. Instead of using cubic splines, where the nodes have to be carefully set, a kernel regression with a cross-validated bandwidth h_CV is performed. Using the Gaussian density as kernel function K(.), the diurnal periodic component can be computed by means of the Nadaraya–Watson estimator

m.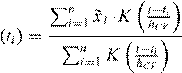

Thus, X_i ≡ D_i/m(t_i); that is, the deseasonalized order duration, should have no diurnalpatternandexhibitaunitmean(seealsoEngleandRussell1998,p.1137).The model is estimated by jointly maximizing the two partial log-likelihood functions of the bivariate model

n

LBIV .

                                                          LACD                                                                                 LACL

To specify the distribution of the standardized durations f_ACD(.), Engle and Russell (1998) use an exponential and a Weibull distribution, whereas other researchers favor more flexible alternatives. In this article, the generalized Beta distribution is used fACD(εi;θ1) = f

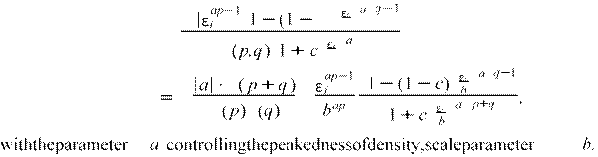                                              |a                         c) _b

                                          =      bap ^B                    _b         p+q

smooth parameter c, and parameters p and q influencing shape and skewness (for statisticalproperties,seeMcDonaldandXu1995;KleiberandKotz2003),whereby θ₁ = {θ_ACD,a,b,c,p,q,δ₁}.Becauseofitsflexibility,thegeneralizedBetadistribution nestsmorethan30distributionsaslimitingorspecialcases,manyofthosediscussed in the ACD literature such as the Burr distributions Type III and Type XII (e.g., Fernandes and Grammig 2006; Lu and Pang 2008), the generalized Gamma, or the generalized Beta of the second kind (a variation of this distribution is also called “generalized F-distribution”; see Hautsch 2004). The moments of ε_i can be obtained by

B

a

with Beta function B(·) and the Gaussian hypergeometric function

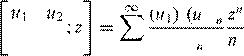2F1      n 2) . v1 n=0 (v1) !

Thus, the log-likelihood of the ACD part with a generalized Beta distribution for the innovations is

LACD = n

n

− ap (q

i=1

 ,

i

where

−1

b,        

yielding a unit expectation as required. To evaluate the ACD model’s diagnostics, one can examine the properties of the standardized duration such as the mean of unity or their autocorrelation structure applying the Ljung–Box test. Furthermore, the theoretical distribution of the residuals implied by the estimated parameters f (ε,θˆ) can be compared with the empirical one ˆf (εˆ). For this purpose, Fernandes and Grammig (2005) develop the D-test to quantify the difference between them, which should be zero under correct model specification. The log-likelihood function of the ACL part is given by

n

LACL,

i=1

with

,

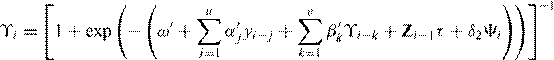and θ₂ = {θ_ACL,δ₂}. To assess the goodness of fit of the dynamic logit model, it is possible to apply the common measures based on modified R²s that are often used in discrete choice models. The literature in categorical data analysis provides a broad spectrum of useful tools (e.g., Hensher, Rose, and Greene 2005; Greene 2008).

IV.  Xetra Order Book and Empirical Results

The order book data analyzed in this study are extracted from the Xetra order book system. Xetra stands for “exchange electronic trading” and is the trading