Does the choice of performance measure influence the evaluation of hedge funds, страница 3

Because LPMs consider only negative deviations of returns from a minimal acceptable return (which could be zero, the risk-free rate, or the average return), they seem to be a more appropriate measure of risk than the standard deviation, which considers negative and positive deviations from expected return (see Sortino and van der Meer, 1991). The choice of order n determines the extent to which the deviation from the minimal acceptable return is weighted. The LPM of order 0 can be interpreted as shortfall probability, LPM of order 1 as expected shortfall, and LPM of order 2 for s ¼ r^d_i as semi-variance. The LPM order chosen should be higher the more risk averse an investor is. Omega (see Shadwick and Keating, 2002), the Sortino ratio (see Sortino and van der Meer, 1991), and Kappa

3 (see Kaplan and Knowles, 2004) use LPMs of order 1, 2, or 3:^[5]rd  s

3 LPM3iðsÞ

Note that these measures compute the excess return as the difference between the average return and the minimal acceptable return. Another way of measuring return is to use a higher partial moment (HPM), which measures positive deviations from the minimal acceptable return s. The upside potential ratio (see Sortino et al., 1999) combines the HPM of order 1 with the LPM of order 2. The advantage of this ratio is the consistent application of the minimal acceptable return in the numerator as well as in the denominator:

Upside potential ratioi ¼ p2HPMffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiLPM1i2ðisðsÞÞ:  ð5Þ

2.2.2. Measuring performance on the basis of drawdown

Drawdown-based measures are particularly popular in practice. They often are used by commodity trading advisors because these measures illustrate what the advisors are supposed to do best – continually accumulating gains while consistently limiting losses (see Lhabitant, 2004).

The drawdown of a security is the loss incurred over a certain investment period. In describing drawdown-based risk measures, r_itT denotes the return realized over the period from t to T (t < T6 T). For all these returns, MD_i1 denotes the lowest return and MD_i2 the second lowest return, and so on. In general, the smallest return, MD_i1, is negative and denotes the maximum possible loss that could have been realized in the considered period of time. The Calmar ratio (see Young, 1991), Sterling ratio (see Kestner, 1996), and Burke ratio (see Burke, 1994) use the maximum drawdown, an average above the N largest drawdowns (which does not react too sensitively to outliers), and a type of variance above the N largest drawdowns (which takes into account that a number of very large losses might represent a greater risk than several small declines) as risk measures:^[6]

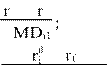d

            Calmar ratio_i ¼      ^{i          f}                                                                                                                                       ð6Þ

                          Sterling ratio ¼;                                                                                                    ð7Þ

                                        2 PN                2

MD

                                              j¼1           ij

2.2.3. Measuring performance on the basis of value at risk