Використання графічних методів лінійного програмування для вирішення задач оперативного планування автомобільних перевезень

Практична робота №1

Тема: Використання графічних методів лінійного програмування для вирішення задач оперативного планування автомобільних перевезень

Мета роботи – Набути практичних навичок з вирішити задач лінійного програмування при перевезенні промислових вантажів з використанням графічного методу.

Завдання:

1.  Для кожного варіанту організації роботи автомобіля на маршрутах розрахувати кількість обертів, час роботи на маршруті та частку невикористаного робочого часу. Результати занести до таблиці

2.  Скласти математичні рівняння для вирішення задачі графічним методом.

3.  За результатами вирішення рівняння на міліметровому папері побудувати графік для визначення кількості обертів на маршрутах.

4.  За графіком обрати оптимальний варіант організації перевезень вантажів, порівняти результат з даними таблиці.

5.  Зробити висновок.

Вихідні дані

Табл. 1 – Час оберту автомобіля, год

Табл. 2 – Час знаходження в наряді, год

Вказівки до виконання

Характер задач, вирішуваних за допомогою лінійного програмування, легше всього проілюструвати графічно. Розглянемо можливості використовування графічного методу для планування роботи автомобілів на кількох прикладах.

Необхідно здійснити перевезення вантажу по двох маршрутах. Час оберту на маршрутах наведено в таблиці 1. Час знаходження автомобіля в наряді, без урахування часу подачі його під перше вантаження і часу повернення в АТП після останнього розвантаження, наведено в таблиці 2.

Необхідно визначити, яку кількість обертів повинен зробити автомобіль на кожному маршруті, щоб його час в наряді був використаний максимально.

Наприклад, для варіанту №00, якщо автомобіль спрямувати на перевезення вантажу по маршруту №1, то він зможе зробити 4 повні оберти, оскільки

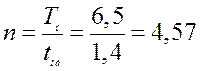,                                                      (1.1)

де       - кількість обертів;

– час в наряді, год;

 – час оберту на маршруті №1, год.

Затрачено буде при цьому 5,6 год. Таким чином, 0,9 год не будуть використані, що складає близько 14,0% загального часу перебування автомобіля в наряді.

Якщо автомобіль спрямувати на перевезення вантажу по маршруту №2, то він, за результатами аналогічних розрахунків, зможе зробити 5 повних обертів, затративши на це 5,5 год. Тут втрати часу складатимуть 1,0 год що більше 15%.

Таких втрат можна уникнути, якщо автомобіль працюватиме спочатку на перевезеннях вантажу на маршруті 1, а потім на перевезеннях вантажу на маршруті 2. Але тоді необхідно визначити, яку кількість обертів він повинен зробити на кожному маршруті. Для цього звичайно потрібно розрахувати всі можливі варіанти роботи автомобіля на двох маршрутах і з цих варіантів вибрати той, який забезпечує якнайменші втрати часу.

Приклад розрахунку варіантів роботи автомобіля на маршрутах приведені в табл. 3.

Таблиця 3 – Приклад розрахунків варіантів роботи автомобіля

Таким чином, виконавши розрахунки по п'яти варіантах, можна бачити, що при другому варіанті, коли автомобіль робить 3 оберти на маршруті 1 і 2 оберти на маршруті 2, його час знаходження в наряді майже повністю буде використаний продуктивно. Щоб це з'ясувати, довелося виконати спеціальні розрахунки, витративши на них певний час. Використовуючи ж графічний метод, можна одержати такий же результат при значно меншій витраті часу на ці обчислення.

Вирішувана задача може бути представлена в наступній математичній формі:

1,4 x₁ +1,1 х₂ ≤6,5

С_max =1,4 х₁×+1,1 х₂

де     x₁ – кількість обертів на маршруті №1;

        х₂ – кількість обертів на маршруті №2.

Якщо розглядати випадки строгої рівності 1,4 x₁ +1,1 х₂ =6,5 то можна побудувати графік.

Візьмемо лист міліметрівки або лист паперу, нанесемо на нього сітку координат. Вісь x₁ означає кількість обертів автомобіля на маршруті №1, а вісь х₂  – кількість обертів на маршруті №2 (рис. 1).

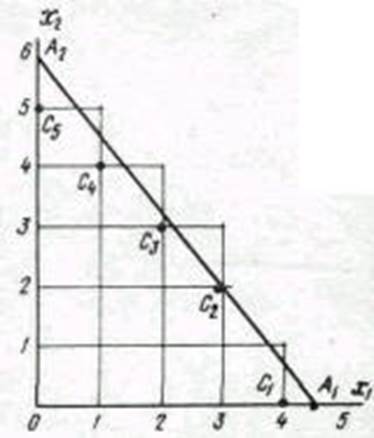
Рис. 1. – Визначення кількості обертів нв маршруті.

Щоб знайти значення x₁  при х₂=0, розділимо вільний член рівняння на коефіцієнт при x₁, тобто 1,4.

6,5/1,4=4,63

Отримане число відкладемо на осі x₁ і позначимо його точкою А₁. Таким же чином знаходимо значення х₂  при х₁=0 і відповідну точку відкладаємо на осі х₂, позначивши її А₂.

З'єднаємо точки А₁ і A₂ прямою. Тепер видно, що можливості використовування часу знаходження автомобіля в наряді обмежені трикутником ОА₁А₂.

Точки С показують, яка ціла кількість обертів по кожному маршруту може бути зроблена за 6,5 год. Нижній індекс при точках С показує, якому варіанту відповідає дана точка. Наприклад, точка C₂ відповідає другому варіанту, С₃ третьому і т.д.

Щоб визначити ту кількість їздок на маршруті, яка забезпечує якнайкраще використовування часу знаходження автомобіля в наряді, достатньо вибрати точку С, що знаходиться найближче до прямої А₁-А₂. Такою точкою на рис. 1 є точка С₂. Вона відповідає в табл. 3 другому варіанту, який є оптимальним. В цьому варіанті слід робити 3 оберти на маршруті №1 і 2 оберти на маршруті №2.

Таким чином, оптимальний план організації перевезень отриманий значно швидше, ніж при розрахунку всіх можливих варіантів, по таблиці 3.

Контрольні питання:

1.  Які основні показники роботи рухомого складу при перевезенні вантажів?

2.  Як знаходиться час оберту автомобіля?

3.  Що таке час роботи на лінії та час в наряді, чим вони відрізняються.

4.  Що таке маршрут перевезення, які є типи маршрутів?