Другие предметы \ Эконометрика

Определение наилучшей корреляционно-регрессионную зависимости. Построение диаграммы

Страницы работы

6 страниц (Word-файл)

Скачать файл

Фрагмент текста работы

Задание 1.

Определить наилучшую корреляционно-регрессионную зависимость по следующим основным параметрам (используя метод ранжирования):

– среднему квадратическому отношению уровней;

– коэффициенту тесноты связи;

– достоверности коэффициента тесноты связи (критерий Стьюдента) через отношения с табличным значением;

– средней ошибки аппроксимации;

– достоверности уравнения регрессии (критерий Фишера) через отношения с табличным значением.

Построить диаграмму исследуемых корреляционно-регрессионных зависимостей (диаграмму корреляционно-регрессионных зависимостей построить с использованием компьютера, при этом на графике выделить две наилучшие зависимости). В качестве шкалы деления по осям координат фактора и показателя, использовать только их фактические значения. В корреляционно-регрессионной зависимости с лучшими характеристиками устранить влияние гетероскедастичности.

Варианты задания 1

№	Вариант 1		Вариант 2		Вариант 3
№	Выручка от реализации мебели, тыс. руб.	Спрос на изделия из кожи	Импортное сырье, %	Затраты на рекламу, тыс. руб.	Количество венерических заболеваний	Постоянство партнеров, %
1	8500	100	20	18	10	80
2	9000	200	30	23	20	60
3	7000	300	41	18	30	50
4	6500	400	48	16	15	75
5	4500	250	35	13	40	45
6	3600	150	27	10	60	30
7	7500	800	90	19	50	41
8	4800	500	55	14	30	48
9	9500	350	44	25	45	46
10	4200	250	32	11	50	38
11	7700	600	64	17	15	72
12	8500	700	75	23	55	35
13	9500	550	60	28	5	90
14	8200	450	50	22	25	65
15	9400	510	57	26	35	55
№	Вариант 4		Вариант 5		Вариант 6
№	Количество дорожно-транспортных происшествий	Водитель в нетрезвом состоянии, %	Урожайность картофеля, ц/га	Количество выпавших осадков в год, мм	Курс доллара относительно рубля	Добыча нефти, тыс. т
1	40	20	220	280	30,5	7400
2	55	10	180	240	28,2	8200
3	20	30	140	180	29,6	8000
4	15	60	100	80	31,2	7000
5	70	40	80	100	32,0	6800
6	30	20	280	300	26,5	8700
7	25	15	160	220	22,5	9200
8	45	25	70	70	20,0	10000
9	30	55	50	60	21,0	9500
10	100	45	110	100	26,0	9000
11	120	35	140	150	31,7	7300
12	140	30	200	260	29,5	7900
13	160	80	210	250	27,2	8500
14	90	32	180	220	32,4	7200
15	80	45	150	200	30,8	7200

Задание 2.

Найти нормальные уравнения линейной многофакторной зависимости, уравнение регрессии, множественный коэффициент корреляции, корреляционное отношение, индекс корреляции, коэффициент детерминации, среднюю относительную ошибку аппроксимации, оценить достоверность коэффициента тесноты связи и уравнения регрессии (критерий Фишера), рассчитать прогнозируемое значение показателя.

Используя данные задания 2, рассчитать совокупный коэффициент корреляции через парные значения коэффициентов корреляции и сравнить с рассчитанным в задании 2 множественным коэффициентом корреляции.

Используя данные и расчеты задания 2, дать оценку влияния факторов на результативный показатель, используя понятия коэффициентов эластичности и бета коэффициентов для линейной множественной регрессии.

Определить наиболее существенные факторы, влияющие на результативный показатель, найти форму этой связи и определить прогнозируемое значение показателя (несущественные факторы исключить из корреляционно-регрессионной зависимости). Устранить влияние гетероскедастичности.

Y – валовой доход предприятия, тыс. руб.;

X1 – основные фонды, тыс. руб.;

X2 – количество работающих, чел.;

X3 – ИТР в общем количестве работающих, %;

X4 – количество привлекаемых рабочих со стороны, чел.;

X5 – количество специалистов из-за рубежа, чел.;

X6 – использование оборудования, %;

X7 – износ оборудования, %;

X8 – обеспеченность сырьем, %;

X9 – качество сырья, %;

X10 – импортное сырье в общем количестве сырья, %;

X11 – перебои электроэнергии, час;

X12 – внедрение новых изобретений и предложений НТР.

Варианты работ к заданию 2

№ варианта	Номер задания показателя Y	Номера факторов
1	1	1, 2, 3, 4, 5, 6,7
2	1	1, 2, 3, 4, 8, 9, 10
3	1	1, 2, 3, 4, 10, 11, 12
4	1	2, 3, 4, 5, 6, 7, 8
5	1	2, 3, 4, 5, 8, 9, 10
6	1	2, 3, 4, 5, 10, 11, 12
7	1	3, 4, 5, 6, 7, 8, 9
8	1	3, 4, 5, 6, 9, 10, 11
9	1	3, 4, 5, 6, 10, 11, 12
10	1	4, 5, 6, 7, 8, 9, 10

Варианты значений показателя Y

№	1	2	3	4	5
1	15000	2000	21250	20000	2500
2	25000	2250	23750	40000	3000
3	20000	2500	30000	30000	3500
4	30000	3500	33000	50000	5500
5	40000	3100	29750	70000	4800
6	22000	2850	30000	32000	4300
7	35000	3150	33750	60000	5000
8	28000	3600	37000	46000	5900
9	44000	3800	31500	78000	6100
10	32000	2500	28500	54000	3500
11	18000	3200	37000	26000	4900
12	46000	4200	43000	82000	6900
13	38000	4400	46500	66000	7300
14	50000	4900	40250	90000	8500
15	48000	3150	25750	86000	4800

Варианты значения факторов Х

№	1	2	3	4	5	6	7	8	9	10	11	12
1	3000	44000	30	100	2	40	60	70	40	20	120	1
2	4000	13000	12	2200	4	50	55	45	65	25	110	3
3	4200	30000	11	800	2	45	60	70	80	25	115	2
4	4500	18000	5	3000	4	55	50	25	75	30	105	9
5	5000	25000	40	1200	5	60	45	90	80	35	100	4
6	3500	11000	8	1000	4	40	58	75	70	30	112	2
7	4800	42000	17	1500	5	54	48	82	75	30	102	11
8	4600	14500	25	4100	4	52	45	75	65	30	108	3
9	5500	26000	24	2300	6	65	44	85	80	35	60	4
10	4900	21000	16	2100	5	58	60	80	75	30	100	3
11	3100	17000	11	300	4	42	70	60	50	25	122	1
12	5800	28000	15	2400	6	64	40	85	80	35	55	5
13	5000	24000	22	2900	4	58	44	35	75	35	65	4
14	4300	19000	28	2600	7	70	38	85	80	35	50	6
15	4100	27000	36	450	6	66	40	75	90	35	58	5
Прогноз	4700	23500	18	2500	8	75	35	90	85	40	45	7

Задание 3. Исходные данные представлены в табл. 1. Выявите гетероскедастичность остатков модели и примените обобщенный МНК для ее устранения.

Таблица 1

Размер производства	Прибыль
x	y
5	5
6	7
6	6
10	9
11	15
12	18
12	27
12	23
23	30
24	37
25	39
25	51

Задание 4. По исходным данным (см. табл. 2) по методу максимального правдоподобия для тобит-моделей с помощью программного пакета «Econometric Views» оценены параметры уравнения регрессии:

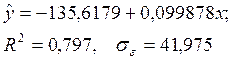
Таблица 2

x	500	1000	1200	1500	1800	2000	2300
y	0	0	0	0	0	110	131

Продолжение

x	2450	2500	2600	2700	2800	3000	3500
y	140	145	150	165	182	180	182

Оцените среднее изменение результата при изменении фактора на одну единицу от среднего уровня.

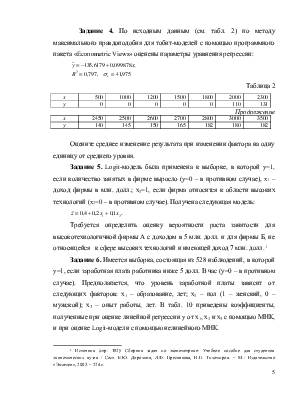
Задание 5. Logit-модель была применена к выборке, в которой y=1, если количество занятых в фирме выросло (y=0 – в противном случае), x₁ – доход фирмы в млн. долл.; х₂=1, если фирма относится к области высоких технологий (x₂=0 – в противном случае). Получена следующая модель:

Требуется определить оценку вероятности роста занятости для высокотехнологичной фирмы А с доходом в 5 млн. долл. и для фирмы Б, не относящейся к сфере высоких технологий и имеющей доход 7 млн. долл.[1]

Задание 6. Имеется выборка, состоящая из 528 наблюдений, в которой y=1, если заработная плата работника ниже 5 долл. В час (у=0 – в противном случае). Предполагается, что уровень заработной платы зависит от следующих факторов: х₁ – образование, лет; х₂ – пол (1 – женский, 0 – мужской); х₃ – опыт работы, лет. В табл. 10 приведены коэффициенты, полученные при оценке линейной регрессии y от х₁, х₂ и х₃ с помощью МНК, и при оценке Logit-модели с помощью нелинейного МНК.

Требуется:

а) определить на основе Logit-модели оценку вероятности для мужчины и для женщины, имеющих 12 лет образования и 15 лет опыта работы, оказаться низкооплачиваемыми работниками;

б) определить на основе Logit-модели изменение оценки вероятности быть