Парная регрессия и корреляция. Спецификация модели парной регрессии. Линейные и нелинейные регрессии

Тема 3. Парная регрессия и корреляция

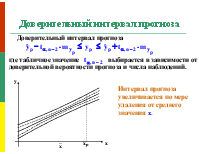
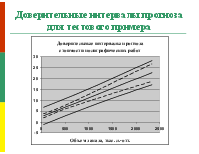
3.1. Спецификация модели парной регрессии 3.2. Оценка параметров парной регрессии и корреляции (идентификация модели) 3.3. Оценка качества эконометрической модели парной регрессии (верификация модели) 3.4. Интервалы прогноза по уравнению регрессии

3.1. Спецификация модели парной регрессии

Спецификация модели – обоснованный с позиций экономической теории выбор вида и структуры модели, отбор факторов и математическое описание характера их влияния на результирующий признак

2

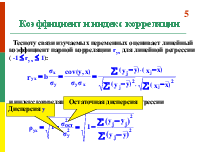
Парная регрессии

Парная регрессия – это уравнение связи двух переменных y и x: y = f (x) + e , где y – зависимая переменная (результативный признак, объясняемая переменная); x – независимая переменная (фактор-аргумент, объясняющая переменная); f(x) – функция регрессии; e – случайная величина (возмущение), отражающая действие не учтенных в функции регрессии факторов случайной природы. Расчетное значении зависимой переменной, вычисляемое с помощью функции регрессии для заданной величины аргумента, будем обозначать , а выражение будем называть теоретическим уравнением регрессии.

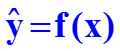
2

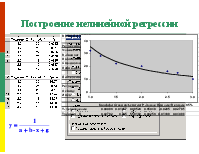
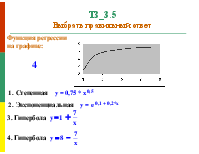
Линейные и нелинейные регрессии

• Различают линейные и нелинейные регрессии. Линейная регрессия записывается в следующем виде:
• y = a + b * x + e
• Нелинейные регрессии делятся на два класса:
• регрессии, нелинейные по объясняющим переменным
• · полиномы вида y = a + b1 * x + b2 * x2 + b3 * x3 + e ;
• · гипербола
• • экспоненциальная y = e a + b * x * e .
• регрессии, нелинейные по оцениваемым параметрам
• · степенная y = a * xb * e ;
• · показательная y = a * bx * e ;

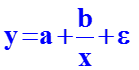
2

Аналитический выбор вида функции регрессии

В парной регрессии выбор вида функции f(x) может быть осуществлен аналитическим или экспериментальным мето-дами. Аналитический метод основан на содержательном ана-лизе экономической природы связи исследуемых признаков. Например, затраты предприятия могут быть подразделены на условно-переменные, изменяющиеся пропорционально изме-нению объема продукции (расход материалов, оплата труда и др.) и условно-постоянные, не меняющиеся с изменением объема производства (арендная плата, содержание админи-страции и др.). Соответственно зависимость затрат на произ-водство y от объема продукции x характеризуется линейной функцией: y = a + b * x , а зависимость себестоимости единицы продукции z от объема продукции – гиперболой:

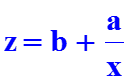
2

Линейная модель парной регрессии

Линейная модель парной регрессии y = a + b*x + e находит широкое применение ввиду четкой экономической интер-претации ее параметров. В линейной модели коэффициент b имеет смысл увеличения переменной y при единичном приращении x:

Знак параметра a интерпретируется как качественный показатель соотношения темпов изменения результата y и фактора x. При a > 0 относительное изменение результата происходит медленнее, чем изменение фактора:

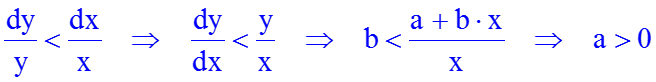
При a < 0 - относительное изменение результата происходит быстрее, чем относительное изменение фактора.

2

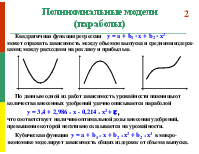
Полиномиальные модели (параболы)

Квадратичная функция регрессии y = a + b1 * x + b2 * x2 может отражать зависимость между объемом выпуска и средними издерж-ками; между расходами на рекламу и прибылью.

По данным одной из работ зависимость урожайности пшеницы от количества внесенных удобрений удачно описывается параболой y = 3,4 + 2,986 * x - 0,214 * x2 + e , что соответствует наличию оптимальной дозы внесения удобрений, превышение которой негативно сказывается на урожайности. Кубическая функция y = a + b1 * x + b2 * x2 + b2 * x3 в микро-экономике моделирует зависимость общих издержек от объема выпуска.

2

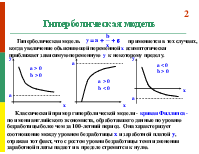
Гиперболическая модель

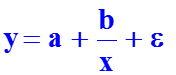
Гиперболическая модель применяется в тех случаях, когда увеличение объясняющей переменной x асимптотически приближает зависимую переменную y к некоторому пределу.

y

y

a

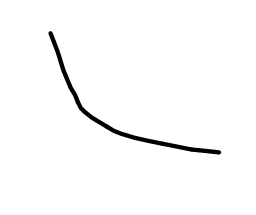
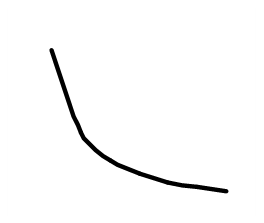
a < 0 b > 0

a > 0 b > 0

a > 0 b < 0

x

a

a

x

x

Классический пример гиперболической модели - кривая Филлипса - по имени английского экономиста, обработавшего данные по уровню безработицы более чем за 100-летний период. Она характеризует соотношение между уровнем безработицы x и заработной платой y, отражая тот факт, что с ростом уровня безработицы темп изменения заработной платы падает и в пределе стремится к нулю.

2

Кривая Энгеля

Гипербола с отрицательным значением коэффициента b известна как кривая Энгеля – по имени немецкого статистика, впервые показавшего зависимость семейных расходов на товары длительного пользования y от величины семейного дохода x Вместе с тем гипербола не является единственно возможной функцией для описания кривой Энгеля. В дальнейшем некоторые исследователи использовали полулогарифмиче-скую кривую y = a + b * lnx + e и получили лучшее совпадение с данными наблюдений.

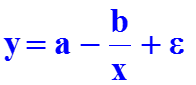
2

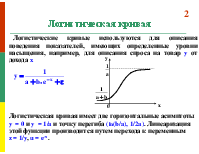
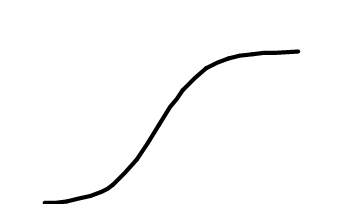
Логистическая кривая

Логистические кривые используются для описания поведения показателей, имеющих определенные уровни насыщения, например, для описания спроса на товар y от дохода x

y

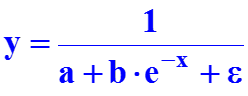
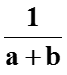
x

0

Логистическая кривая имеет две горизонтальные асимптоты