Моменты распределения. Показатели формы распределения. Относительный показатель квартильной вариации

9. Моменты распределения. Показатели формы распределения

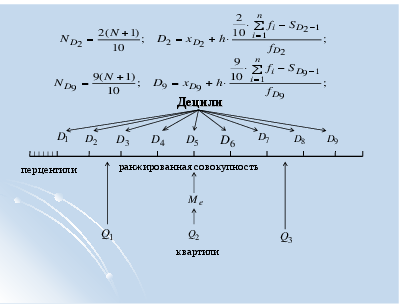
Если в качестве показателя центра распределения используется медиана, то для характеристики вариации признака в совокупности используется квартильное отклонение , где - соответственно первая и третья квартили распределения. также можно использовать вместо размаха вариации, чтобы избежать недостатков, связанных с использованием крайних значений. Квартили – это значения признака в ранжированном ряду распределения, выбранные таким образом, что 25% единиц совокупности будут меньше по величине ; 25% единиц будут заключены между и ; 25% – между и остальные 25% превосходят .

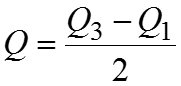
Расчетные формулы: ; В симметричных и умеренно симметричных распределениях . Квартильное отклонение вычисляют в тех случаях, когда найти трудно или невозможно. Если , то распределение несимметричное.

• Относительный показатель квартильной вариации:
• Анализ вариации в рядах распределения полезно дополнить показателями дифференциации:
• Коэффициент фондовой дифференциации: , где – среднее из 10% наибольших значений признака, – среднее из 10% наименьших значений признака;
• Коэффициент децильной дифференциации: , где – девятая дециль, – первая дециль.
• Расчетные формулы для децилей при предположении равномерного наращивания величины интервала на каждую единицу частоты:

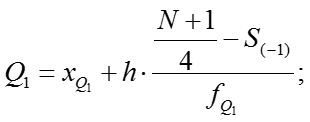
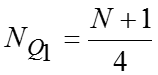
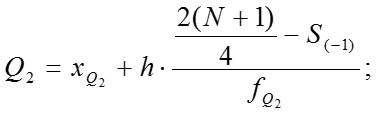
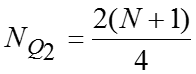
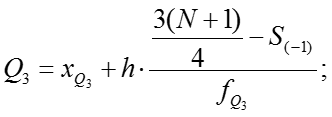
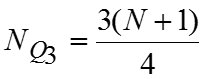
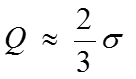
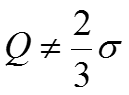
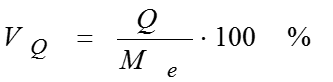
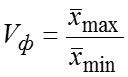
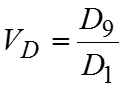
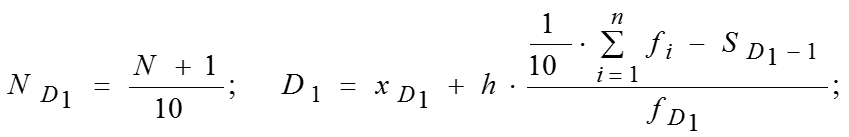
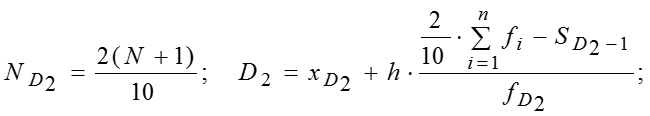
Децили

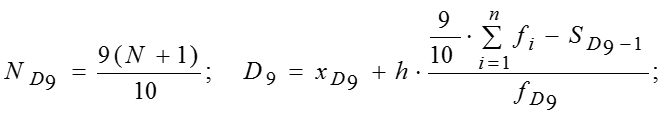
ранжированная совокупность перцентили

квартили

Пример. Пусть известны размеры прибыли 20 банков за год (млрд. руб): 3,7; 4,3; 6,7; 5,6; 5,1; 8,1; 4,6; 5,7; 6,4; 5,9; 5,2; 6,2; 6,3; 7,2; 7,9; 5,8; 4,9; 7,6; 7,0; 6,9. Количество групп по формуле Стерджесса: Размах вариации: . Шаг: . Тогда составим интервальный вариационный ряд:

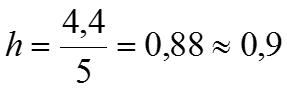
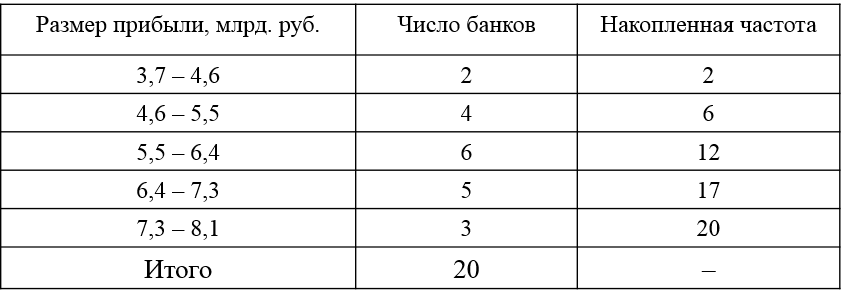
млрд. руб. – наиболее часто встречающийся размер прибыли. млрд. руб. – значение размера прибыли для среднего (по номеру) банка в ранжированном ряду. млрд. руб.; млрд. руб. млрд. руб.

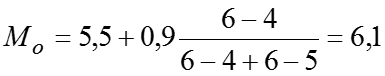
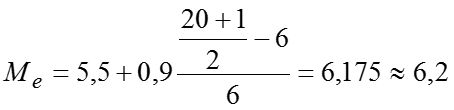
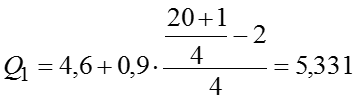
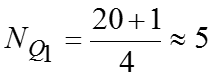
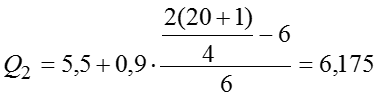
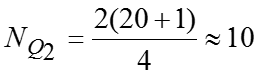
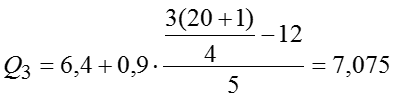
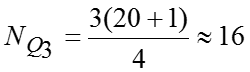
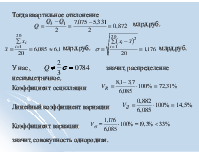
Тогда квартильное отклонение млрд.руб. млрд.руб. млрд.руб. У нас , значит, распределение несимметричное. Коэффициент осцилляции Линейный коэффициент вариации Коэффициент вариации значит, совокупность однородная.

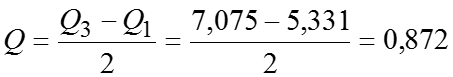
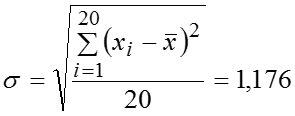
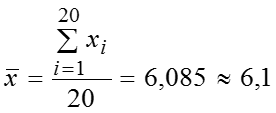
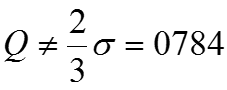
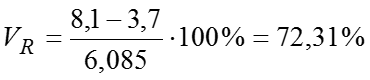
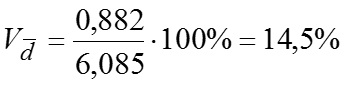
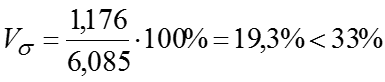
Относительный показатель квартильной вариации Коэффициент фондовой дифференциации это значит, что размер прибыли у 10% банков с наибольшими доходами в 2 раза превышает размер прибыли у 10% банков с наименьшими доходами.

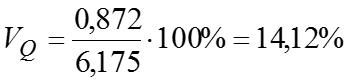
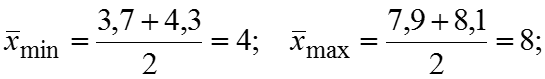
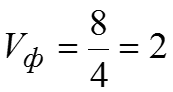
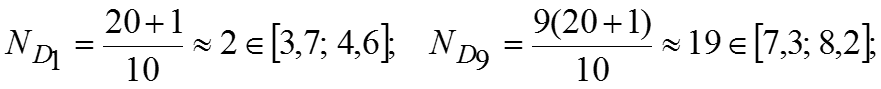
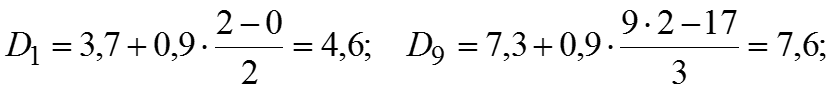
Коэффициент децильной дифференциации , то есть наименьший размер прибыли 10% банков и наибольший размер прибыли 10% банков отличаются в 1,652 раза.

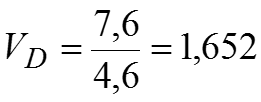
Моменты распределения

Моментом распределения называется средняя арифметическая тех или иных степеней отклонения индивидуальных значений признака от определенной исходной величины , где – порядок момента, А – величина, от которой определяются отклонения. Начальные моменты вычисляются при А=0:

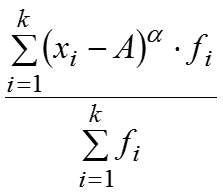
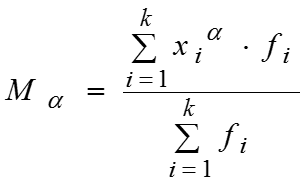
Центральные моменты вычисляются при : Условные моменты вычисляются при : Условные моменты вычисляются при ;

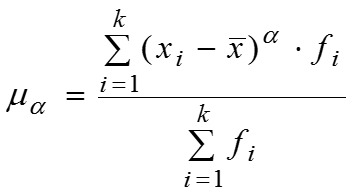
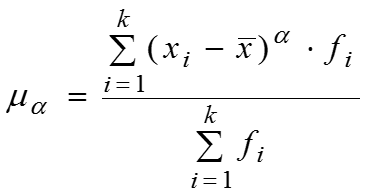
самостоятельного значения не имеют, но применяются для упрощения вычисления центральных моментов. Например, . Кривая распределения характеризует теоретическое распределение, т.е. то распределение, которое получилось бы при полном погашении всех случайных причин, искажающих основную закономерность. Показатель асимметрии . Для симметричных распределений .

• Для правосторонней асимметрии и кривая распределения выглядит так:

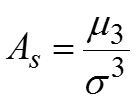
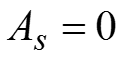
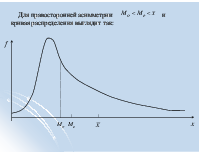
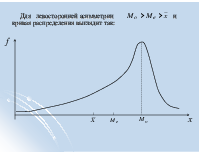
Для левосторонней асимметрии и кривая распределения выглядит так:

• Оценка степени существенности этого показателя дается с помощью средней квадратической ошибки, которая зависит от объема наблюдений и рассчитывается по формуле:
• , если
• , то асимметрия существенна и распределение признака в генеральной совокупности не является;
• ,то асимметрия несущественна, ее наличие может быть объяснено влиянием различных случайных обстоятельств.

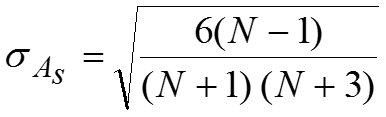
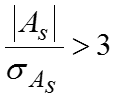
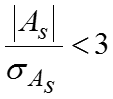
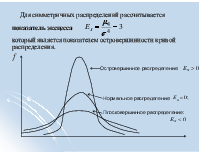
Для симметричных распределений рассчитывается показатель эксцесса который является показателем островершинности кривой распределения.

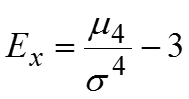
Островершинное распределение:

Нормальное распределение:

Плосковершинное распределение:

Среднеквадратическая ошибка эксцесса Чаще всего в качестве теоретического распределения используется нормальное распределение: .

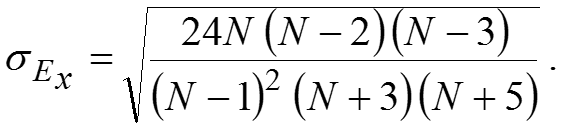
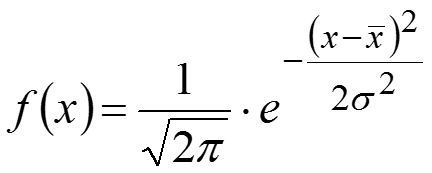
Показатели формы распределения. Точечное оценивание числовых характеристик значений признака

Кривая распределения характеризует теоретическое распределение, т.е. то распределение, которое получилось бы при полном погашении всех случайных причин, искажающих основную закономерность. Начальный момент первого порядка называется выборочным средним, выборочным математическим ожиданием или средним арифметическим выборки. Математическое ожидание характеризует положение распределения на оси X.

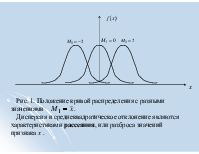
Рис. 1. Положение кривой распределения с разными значениями . Дисперсия и среднеквадратическое отклонение являются характеристиками рассеяния, или разброса значений признака х .

.

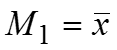
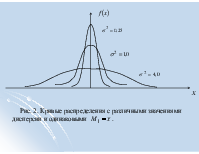
Рис. 2. Кривые распределения с различными значениями дисперсии и одинаковыми