































1.РЯДЫ ДИНАМИКИ
1.1. Основные определения
Ряд динамики – ряд расположенных в хронологической последовательности числовых значений статистического показателя, характеризующих изменение общественных явлений во времени.
Уровни ряда динамики– это числовые значения показателя. Начальным
уровнем ряда ![]() (или
(или
![]() )
называется первый член ряда, последнее в ряду значение
)
называется первый член ряда, последнее в ряду значение ![]() называется
конечным уровнем ряда динамики.
называется
конечным уровнем ряда динамики.
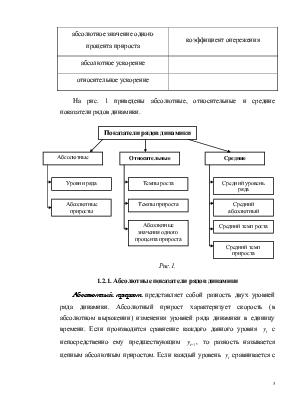
Виды рядов динамики |
|||
|
|
|||
По виду показателей уровня |
По способу фиксирования времени |
В зависимости от расстояния между уровнями |
В зависимости от наличия тренда |
ряды абсолютныхряды относительныхряды средних величин |
моментные интервальные |
с равноотстоящими с неравноотстоящими уровнями во времени |
стационарные нестационарные |
Показатели интенсивности изменения во времени |
Средние показатели |
|
абсолютный прирост |
средний уровень ряда |
коэффициент роста |
средний абсолютный прирост |
темп роста |
средний темп роста |
темп прироста |
средний темп прироста |
абсолютное значение одного процента прироста |
коэффициент опережения |
абсолютное ускорение |
|
относительное ускорение |
На рис. 1 приведены абсолютные, относительные и средние показатели рядов динамики.
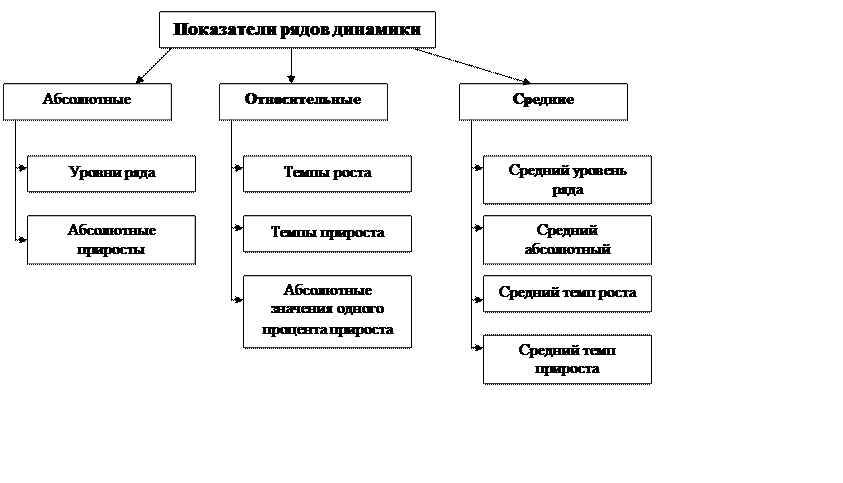
 Рис.1.
Рис.1.
1.2.1. Абсолютные показатели рядов динамики
Абсолютный приростпредставляет собой разность двух
уровней ряда динамики. Абсолютный прирост характеризует скорость (в абсолютном
выражении) изменения уровней ряда динамики в единицу времени. Если производится
сравнение каждого данного уровня ![]() с
непосредственно ему предшествующим
с
непосредственно ему предшествующим ![]() ,
то разность называется цепным абсолютным приростом. Если каждый уровень
,
то разность называется цепным абсолютным приростом. Если каждый уровень ![]() сравнивается
с начальным или каким-либо другим, принятым за постоянную базу сравнения, то
получаются базисные абсолютные приросты.
сравнивается
с начальным или каким-либо другим, принятым за постоянную базу сравнения, то
получаются базисные абсолютные приросты.
На рис. 2 проиллюстрирована процедура нахождения цепных и базисных показателей динамики.
 |
![]()
![]()
![]()
![]()
![]()
![]()
Рис. 2.
Абсолютный прирост
- цепной
![]()
- базисный при начальном уровне ряда у0
![]()
при начальном уровне ряда у1
![]()
где у1- уровень ряда динамики в i-й момент или за i-й период времени; уi-1- уровень ряда в (i-1)-й момент или за (i-1)-й период времени.
Сумма цепных приростов за определенный период времени равна базисному абсолютному приросту за весь этот период или разности между конечным и начальным уровнями ряда динамики:
при начальном уровне ряда у0
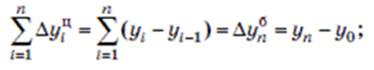
при начальном уровне ряда у1
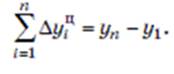
![]()
![]()
Относительные показатели рядов динамики
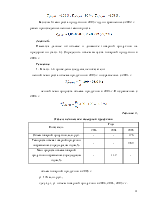
Темп ростапредставляет собой отношение двух уровней ряда динамики. Темпы роста могут быть вычислены с переменной и постоянной базой сравнения. Первые называются цепными, вторые – базисными.
Коэффициент роста
Цепной Базисный
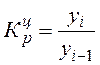
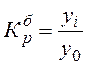
Темп роста
- цепной
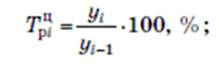
- базисный
При начальном уровне ряда у0
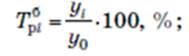
При начальном уровне ряда у1
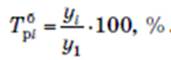
Темп прироста представляет собой отношение абсолютного прироста к уровню динамики, по сравнению с которым он рассчитан. Для ряда динамики темпы прироста могут быть вычислены с переменной базой сравнения, они называются цепными, и с постоянной – базисными.
Темп прироста
- цепной
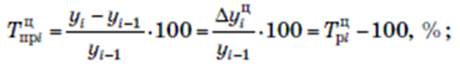
- базисный
При начальном уровне ряда у0
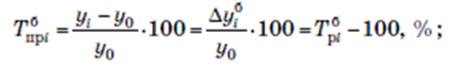
При начальном уровне ряда у1
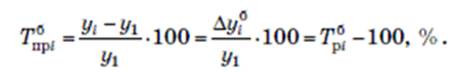
Коэффициент прироста ![]()
Абсолютное значение одного процента прироста представляет собой соотношение абсолютного прироста к темпу прироста, выраженному в процентах
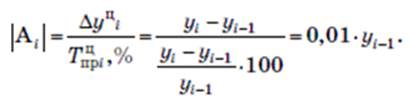
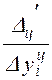
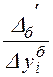
1.2.2. Средние показатели рядов динамики
Средний уровеньряда представляет собой среднюю хронологическую величину из уровней ряда динамики. Рассчитывается для интервальных и моментных рядов с равными и неравными интервалами времени.
В интервальном ряду средняя хронологическая
- невзвешенная (для ряда с равными интервалами)
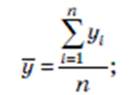
- взвешенная (для ряда с неравными интервалами)
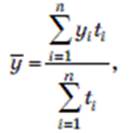
где уi – значение уровня ряда на i-м интервале; ti – продолжительность i-го интервала времени.
В моментном ряду средняя хронологическая
- невзвешенная (для ряда с равноотстоящими моментами времени при начальном уровне ряда у0
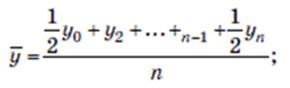
при начальном уровне ряда у1
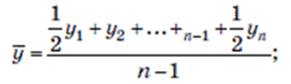
- взвешенная (для ряда с неравноотстоящими моментами времени)
при начальном уровне ряда у0
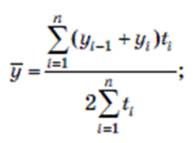
при начальном уровне ряда у1
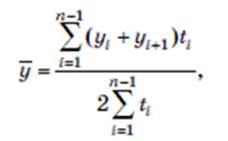
Где у1- уровень ряда в i-й момент времени; ti- период времени
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.