Методы многомерного статистического анализа и моделирования социально-экономических явлений

Методы многомерного статистического анализа и моделирования социально-экономических явлений

Корреляционный анализ

Корреляционный анализ является одним из методов статистического анализа взаимозависимости нескольких признаков.

Основная задача корреляционного анализа состоит в оценке корреляционной матрицы генеральной совокупности по выборке и определении на основе этой матрицы частных и множественных коэффициентов корреляции и детерминации.

Парный и частный коэффициенты корреляции характеризуют тесноту линейной зависимости между двумя переменными соответственно на фоне действия и при исключении влияния всех остальных показателей, входящих в модель. Они изменяются в пределах от -1 до +1, причем чем ближе коэффициент корреляции к 1, тем сильнее зависимость между переменными. Если коэффициент корреляции больше нуля, то связь положительная, а если меньше нуля — отрицательная.

Множественный коэффициент корреляции характеризует тесноту линейной связи между одной переменной (результативной) и остальными, входящими в модель; он изменяется в пределах от 0 до 1.

Квадрат множественного коэффициента корреляции называется множественным коэффициентом детерминации. Он характеризует долю дисперсии одной переменной (результативной), обусловленной влиянием всех остальных переменных (аргументов), входящих в модель.

Исходной для анализа является матрица (1.1)

размерности п*k:, i-я строка которой характеризует i-е наблюдение (объект) по всем k показателям (j = 1,2, ..., k).

В корреляционном анализе матрицу X рассматривают как выборку объема п из k-мерной генеральной совокупности, подчиняющейся k-мерному нормальному закону распределения.

По выборке определяют оценки параметров генеральной совокупности, а именно: вектор средних х, вектор средних квадратических отклонений s и корреляционную матрицу R порядка k: (1.2)

х_ij— значение i-го наблюдения j-го фактора;

г_il — выборочный парный коэффициент корреляции, характеризующий тесноту линейной связи между показателями х_j и х_l. При этом г_il является оценкой генерального парного коэффициента корреляции.

Матрица R является симметричной (г_jl = г_lj) и положительно определенной.

Кроме того, находятся точечные оценки частных и множественных коэффициентов корреляции любого порядка. Например, частный коэффициент корреляции (k - 2)-го порядка между переменными х₁ и х₂  равен (1.3)

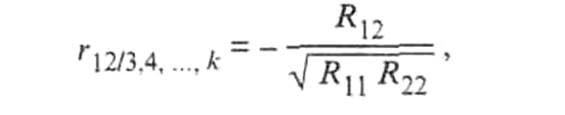
где R_jl — алгебраическое дополнение элемента г_jl корреляционной матрицы R. При этом, где М_jl — минор, т.е. определитель матрицы, получаемой из матрицы R путем вычерчивания j-й строки и l-го столбца.

Множественный коэффициент корреляции (k - 1)-го порядка результативного  признака х₁ определяется по формуле (1.4)

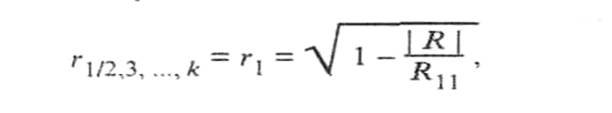
где | R |— определитель матрицы R.

Значимость частных и парных коэффициентов корреляции, т.е. гипотеза H₀:ρ = 0, проверяется по t-критерию Стьюдента. Наблюдаемое значение критерия находится по формуле (1.5)

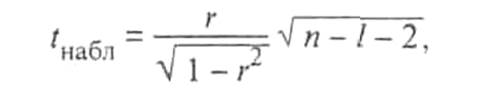
где г — соответственно оценка частного или парного коэффициента корреляции р; / — порядок частного коэффициента корреляции, т.е. число фиксируемых факторов (для парного коэффициента корреляции l = 0).

Проверяемый коэффициент корреляции считается значимым, т.е. гипотеза H_0:р = 0 отвергается с вероятностью ошибки α, если