Аналогично величина основных производственных фондов зависит от размера инвестиций не только текущего года, но и предыдущих лет. В этом случае строятся модели с лаговыми объясняющими переменными. Например,
![]() , где
, где ![]() -
потребление в период времени
-
потребление в период времени ![]() ;
; ![]() -
доход в период времени
-
доход в период времени ![]() ;
;
![]() -
доход в предыдущий период
-
доход в предыдущий период ![]() .
.
В данной модели
лаговой является переменная уt-1, т.е. доход за предыдущий период времени. Возможна ситуация,
когда объясняющая переменная ![]() влияет
на результат
влияет
на результат ![]() не
сразу же, а с определенным запаздыванием во времени, превышающим один временной
интервал. Так, выпуск специалистов высшей квалификации зависит от приема в вузы
четырех – пятилетней давности.
не
сразу же, а с определенным запаздыванием во времени, превышающим один временной
интервал. Так, выпуск специалистов высшей квалификации зависит от приема в вузы
четырех – пятилетней давности.
Объясняющие
переменные, взятые в модели регрессии с запаздыванием во времени, называются лаговыми
переменными. Величина интервала запаздывания называется лагом. Так в
модели ![]() лаговая
переменная взята с лагом, равным 4.
лаговая
переменная взята с лагом, равным 4.
Вместе с тем в правой части модели лаговой может быть и зависимая переменная.
Модели регрессии по временным рядам с лаговыми переменными принято называть динамическими моделями. Их можно подразделить на три класса:
1) модели с лаговыми объясняющими переменными, или, иначе, модели с распределенными лагами:
![]() ;
;
2) модели с лаговыми зависимыми переменными – модели авторегрессии:
![]() ;
;
3) модели с лаговыми зависимыми и независимыми переменными, т.е. авторегрессионные модели с распределенными лагами:
![]() .
.
Выбор величины
лага и количества лагов проводится обычно экспериментально: строятся модели с
разным числом лагов и их величиной и изучается значимость коэффициентов
регрессии при лаговых переменных; останавливаются на модели, для которой все
коэффициенты регрессии при лаговых переменных будут статистически значимыми по ![]() -критерию
Стьюдента.
-критерию
Стьюдента.
1. Модели с распределенными лагами
Модели с распределенными лагами бывают двух типов:
- с конечным числом лагов:
![]() ;
;
- с бесконечным числом лагов:
![]() .
.
Практическое применение чаще всего имеют модели с конечным числом лагов, т.е. модели, в которых число лагов экспериментально определено.
Предположим
рассматривается модель, в которой ![]() ,
т.е.
,
т.е. ![]() .
Данная модель означает, что изменение во времени
.
Данная модель означает, что изменение во времени ![]() объясняющей
переменной
объясняющей
переменной ![]() будет
влиять на значения результативного признака
будет
влиять на значения результативного признака ![]() в
течении 4 следующих моментов времени.
в
течении 4 следующих моментов времени.
Коэффициент ![]() называют
краткосрочным мультипликатором, так как он характеризует среднее изменение
результата
называют
краткосрочным мультипликатором, так как он характеризует среднее изменение
результата ![]() при
изменении
при
изменении ![]() на
1 единицу своего измерения в фиксированный момент времени
на
1 единицу своего измерения в фиксированный момент времени ![]() .
.
В момент времени ![]() воздействие
объясняющей переменной
воздействие
объясняющей переменной ![]() на
результат
на
результат ![]() составит
составит
![]() единиц,
а в момент времени
единиц,
а в момент времени ![]() общее
изменение
общее
изменение ![]() составит
составит
![]() единиц.
единиц.
Любую сумму
коэффициентов ![]() ,
где
,
где ![]() называют
промежуточным мультипликатором, а сумму всех коэффициентов регрессии
называют
промежуточным мультипликатором, а сумму всех коэффициентов регрессии ![]() -
долгосрочным мультипликатором, который характеризует общее изменение
-
долгосрочным мультипликатором, который характеризует общее изменение ![]() через
через
![]() интервалов
времени под воздействием изменения
интервалов
времени под воздействием изменения ![]() в
момент
в
момент ![]() на
1 единицу.
на
1 единицу.
При ![]() долгосрочный
мультипликатор составит
долгосрочный
мультипликатор составит ![]() .
Он характеризует общее среднее изменение
.
Он характеризует общее среднее изменение ![]() через
4 временных интервала при увеличении
через
4 временных интервала при увеличении ![]() в
момент времени
в
момент времени ![]() на
1 единицу, а промежуточные мультипликаторы:
на
1 единицу, а промежуточные мультипликаторы:
![]() -
изменение
-
изменение ![]() в
момент времени
в
момент времени ![]() ;
;
![]() -
изменение
-
изменение ![]() в
момент времени
в
момент времени ![]() ;
;
![]() -
изменение
-
изменение ![]() в
момент времени
в
момент времени ![]() .
.
Если все
коэффициенты регрессии имеют одинаковые знаки, т.е. характеризуются
однонаправленным изменением ![]() в
исследуемые
в
исследуемые ![]() моментов
времени, то можно определять относительные коэффициенты модели
моментов
времени, то можно определять относительные коэффициенты модели ![]() ,
т.е.
,
т.е. 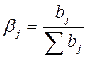 ,
где
,
где ![]() , а
, а
![]() .
Иными словами,
.
Иными словами, ![]() характеризует
долю общего изменения
характеризует
долю общего изменения ![]() в
момент времени
в
момент времени ![]() .
.
Модель с конечным числом лагов при правильной ее спецификации может быть оценена обычным МНК. В этом случае в уравнении:
![]()
переменные ![]() рассматриваются
как объясняющие переменные обычной множественной регрессии.
рассматриваются
как объясняющие переменные обычной множественной регрессии.
Вместе с тем применение МНК к моделям с конечным числом лагов может быть реально затруднено ввиду следующих причин:
1)
при
наличии тенденции переменные ![]() тесно
связаны между собой, что вызывает мультиколлинеарность факторов, которая может
привести к неинтерпретируемым знакам у коэффициентов регрессии и к снижению их
точности;
тесно
связаны между собой, что вызывает мультиколлинеарность факторов, которая может
привести к неинтерпретируемым знакам у коэффициентов регрессии и к снижению их
точности;
2) возможна автокорреляция остатков, так как МНК применяется к временным рядам с тенденцией.
Поэтому нередко для оценки параметров модели с распределенным конечным числом лагов используются специальные методы преобразования, как и для модели с бесконечным числом лагов. Разработаны разные методы оценивания параметров моделей с распределенными лагами, которые учитывают характер распределения коэффициентов регрессии при лаговых объясняющих переменных. Иными словами, методы оценивания параметров модели с распределенными
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.