Формализация задач. Математическое моделирование технических систем. Этапы формализации, страница 3

В широком смысле слова математическое моделирование – это метод познания (исследования), который включает построение модели, ее дальнейший анализ и интерпретацию полученных результатов, в узком – только метод составления модели или только метод ее анализа.

Другими словами: существуют прямая и обратная задачи моделирования, то есть анализ модели и ее синтез. Задача анализа модели, фактически, приводится к той или иной проблеме, характеризующей данный класс математических структур. Задача синтеза состоит в том, что необходимо по известным результатам анализа или измерений построить модель (определить параметры модели и ее структуру).

В общем случае в процессе подготовки и проведения математического моделирования выделяют следующие этапы:

1. абстрагирование: сосредоточение на свойствах, которые являются общими для многих объектов или ситуаций материального мира, и отвлечение от существующих между ними различий;
2. представление: выбор определенного множества средств (символов, графических образов и т.п.) для изображения абстрактных понятий; представление используется также как средство общения;
3. манипуляция: правила преобразования символьного представления как средство предвидения результата аналогичных манипуляций в реальном мире;
4. интерпретация: процесс, обратный формализации;
5. аксиоматизация: строгое формулирование тех свойств, которые были выведены из реального мира, и которые являются общими при манипуляциях, как в материальном мире, так и над абстрактными символами, представляющими реальный мир.

Первый и частично второй этап относятся к процессу формализации задач, второй и третий – собственно к моделированию задач, то есть к формированию моделей, их преобразованию и анализу, пятый – к обоснованию методов моделирования и подготовки «плацдарма» для их дальнейшего развития и усовершенствования. На последних этапах производится попытка сконцентрировать основные фактические сведения об объектах или ситуациях, охваченных этим абстрактным понятием, в нескольких кратких, но мощных аксиомах и потом (имея в виду истинность аксиом) строго доказать, что выводы, полученные в результате манипуляций с этими абстрактными понятиями, являются справедливыми и для прообразов реального мира.

Как вывод, подчеркнем, что специфика автоматизации математического моделирования ТС состоит в том, что здесь должны объединяться знания, с одной стороны, о конкретных технических системах, с другой стороны – знание собственно математических методов, и, наконец, знание и умение использовать компьютерную технику как инструмент моделирования.

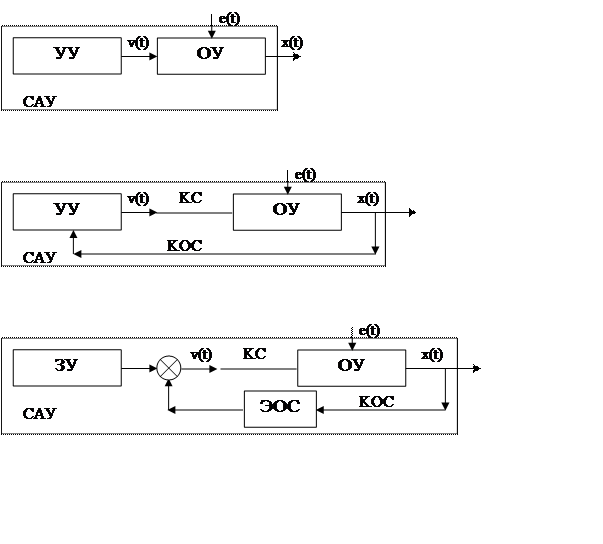x(t) – физическая величина, характеризующая состояние технического объекта (выходная величина объекта);

v(t) – управляющее действие (входная величина объекта);

e(t) -  внешние воздействия;

ОУ – объект управления;

УУ – устройство управления;

САУ – система автоматического управления;

ЗУ – задающее устройство;

КС – канал связи;

КОС – канал обратной связи;

ЭОС – элемент обратной связи;

Рисунок 1 – Примеры формализованного описания технических систем.