Случайные процессы и их воздействие на ЛИС-цепи. Спектральная плотность мощности

Случайные процессы и их воздействие на ЛИС-цепи.

Задание:

  На вход заданной ЛИС-цепи воздействуют заданный сигнал и стационарный аддитивный белый гауссовский шум с нулевым математическим ожиданием и спектральной плотностью мощности (Вт/Гц).

Требуется:

·  Найти отношение сигнал/шум по напряжению и по мощности на входе цепи (для выполнения этого пункта задания считать полосу частот входного шума ограниченной и равной 30 МГц).

Для того чтобы найти заданное отношение, необходимо знать значения таких величин, как D – центральный момент 2-ого порядка (дисперсия) и  σ – среднеквадратическое отклонение.  

Рассмотрим математическую модель белого шума, который представляет собой стационарный случайный процесс с нулевым средним, имеющий АКФ вида 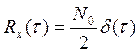. С учетом стробирующего свойства δ-функции можно записать

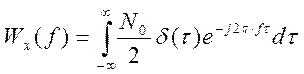, где W_x(ƒ) – спектральная плотность мощности (СПМ).

В случае белого шума СПМ постоянна на всех частотах от  –∞  до  ∞:

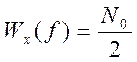
Найдём значение дисперсии:

По теореме Винера - Хинчина

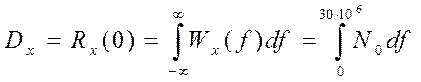
, соответственно отклонение от математического ожидания .

Откуда находим, что отношение сигнал/шум равно:

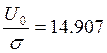 - по напряжению,

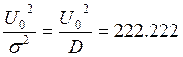 - по мощности.

·  Найти СПМ шума и ОСШ по напряжению и по мощности на выходе цепи.

Отклик ЛИС-цепи на стационарный случайный процесс имеет спектральную плотность мощности, равную входной СПМ, умноженной на квадрат модуля КЧХ (т.е. на квадрат АЧХ) цепи:

Амплитудно-частотная характеристика  цепи была найдена в РГЗ№1:

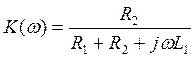
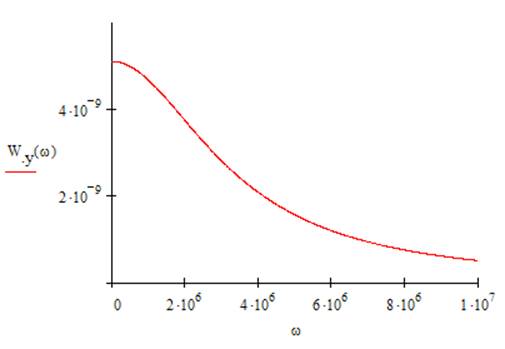
Найдем  и получим график СПМ выходного шума

Найдём отношение сигнал/шум по напряжению и по мощности:

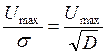, где 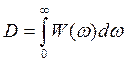. Значение  берём равным (из графика в РГЗ№1).

Получаем: 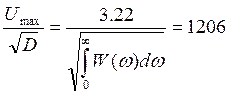 - ОСШ по напряжению.

ОСШ по мощности находим аналогично, возведя в квадрат числитель и знаменатель:

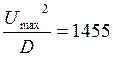 - ОСШ по мощности.

·  Найти эффективную ширину спектра и интервал корреляции шума на выходе цепи.

По графику СПМ выходного шума найдем максимальное значение .

Эффективная ширина спектра может быть определена по формуле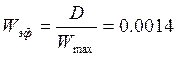

Найдем интервал корреляции:

Случайные процессы, как правило, обладают следующим свойством: их функции корреляции стремятся к нулю с увеличением временного сдвига τ. Числовой характеристикой, служащей для оценки «скорости изменения» реализаций случайного процесса, является интервал корреляции τ_к, определяемый выражением

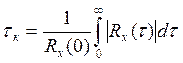
На практике удобнее воспользоваться другим определением, по которому интервал корреляции – такое значение τ, при котором АКФ спадает до заданного уровня, например до 1/10 максимального значения.

Построим график АКФ

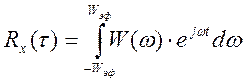
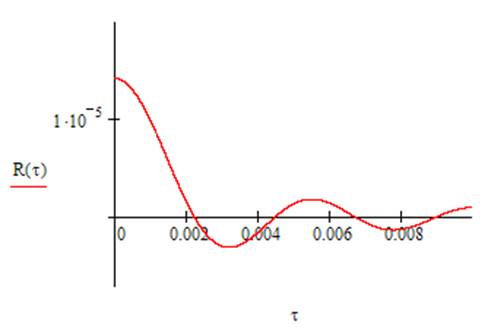
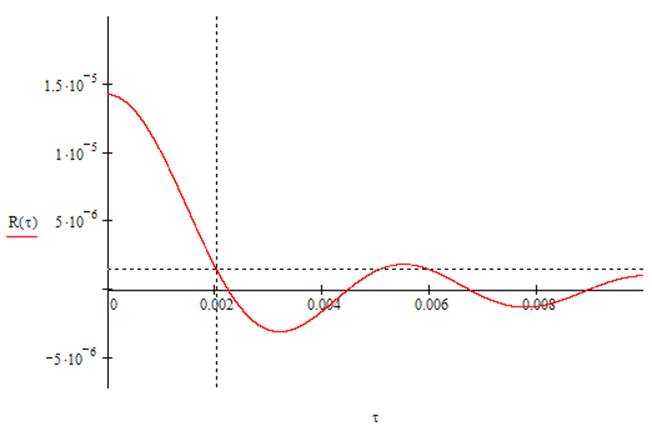
Интервал корреляции определим как время, за которое корреляционная функция становится равна 0.1R_max(τ),  соответственно τ_к = 0.00204

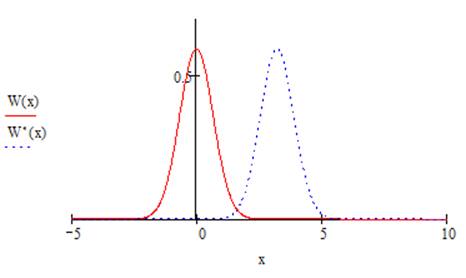
·  Построить графики плотности распределения вероятности мгновенного значения шума и смеси сигнала с шумом на выходе цепи для момента времени, когда сигнал максимален.

Для определения плотности распределения вероятности шума воспользуемся формулой гауссова распределения с ПРВ

 

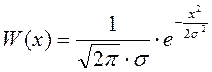
Формула ПРВ для мгновенного значения сигнала с шумом на выходе цепи в момент времени, когда сигнал максимален примет вид

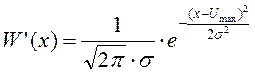
Графики имеют вид:

·  Определить вероятности событий, состоящих в том, что шумовое напряжение в некоторый момент времени превысит заданный порог  и в том, что смесь сигнала с шумом окажется ниже порога (момент времени должен соответствовать максимальному значению сигнала на выходе цепи).

Вероятность события, состоящего в том, что шумовое напряжение в некоторый момент времени превысит заданный порог может быть вычислена по формуле:

.

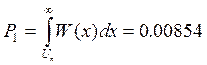В свою очередь, вероятность события, состоящего в том, что смесь сигнала с шумом окажется ниже порога

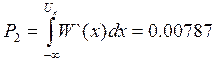
Модулированные колебания.

Задание 1:

  Несущее гармоническое колебание, имеющее амплитуду , частоту , и начальную фазу  модулируется по амплитуде гармоническим колебанием, имеющим частоту , амплитуду  и начальную фазу  (все параметры даны в таблице исходных данных).

Требуется:

·  Найти спектр амплитудно-модулированного колебания.

Амплитудная модуляция заключается в изменении амплитуды несущего гармонического колебания

в соответствии с изменениями первичного (информационного) сигнала. Амплитудно-модулированное колебание имеет вид

, где M – коэффициент модуляции, вычисляемый по формуле 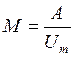. В нашем случае М=0.577

Спектр – это совокупность коэффициентов, определяющих амплитуды гармонических колебаний, составляющих рассматриваемое колебание. Спектр амплитудно-модулированного колебания состоит из трёх гармоник: несущей и двух боковых. Боковые отстают и опережают несущее на величину .

«Найти спектр» означает представить АМК в виде суммы гармонических