Принцип спутниковой связи и ее общая характеристика. Принцип СС, структура радиолинии, определения

Плотность водяного пара (абсолютная влажность), г/м³                                                                                                                                                                                                                                                                     ρ( )h = ψ_ρ( )h

1                                                      10                                     f, ГГц 100

Рис.9

3.Аппаратурные потери

3.1.Потери за счет неточного наведения антенн

Ширина диаграммы направленности по уровню половинной мощности, град

 λ -длина волны

D        D -диаметр  антенны

Потери усиления из-за неточного  наведения

2

⎛ θ ⎞

(6)     Δ =G 12_{⎜                                                                                                                ⎟}

⎝ 2θ0.5 ⎠

3.2.Потери поляризационного рассогласования

                                                                                                                                                                     G     G

                                                                                                        Осевое отношение          r = E_a / E_b ≥1

Пример:

Линейная поляризация: r=oo

Круговая поляризация: r=1

			Волна
		В	Г	ПВ	ЛВ
	В	1	0	0.5	0.5
	Г	0	1	0.5	0.5
	ПВ	0.5	0.5	1	0
	ЛВ	0.5	0.5	0	1

Фактор согласованности двух поляризаций («+»сонаправленное вращение, «-» -противонаправленное):

(r1 ±r2 )² + (1−r1² )(1−r2² )cos² (τ1 −τ2 )          (7) p =       _{2             2}

(1+ r₁ )(1+ r₂ )

р=1 – полное согласование р=0 – полное рассогласование

Поляризационная развязка

p|| X =

2                 2              2           2 (r + r ) + (1−r )(1−r )cos (τ −τ ) = 1                 2                    1              2                  1        2

(8)

Рис.12

2             2             2             2 p₊             (r₁ −r₂ ) +(1−r₁ )(1−r₂ )cos (τ₁ −τ₂ )

Лекция 5 (4 часа). Методы модуляции и помехоустойчивого кодирования

1.Введение в цифровую модуляцию и помехоустойчивое кодирование

1.1.Место модуляции и помехоустойчивого кодирования в спутниковой радиолинии

1.2.Аналоговые и цифровые (двоичные) сообщения

Рис.2

1.3.Форматы кодирования аналогового и цифрового сообщений

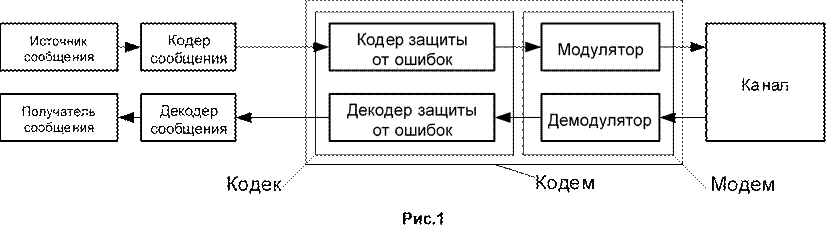
Кодирование (сжатие) аналогового сообщения              Кодирование цифрового сообщения

Источник	Стандарт	Скорость	Задержка накопления	Качество
Источник речевого сообщения	G.729,G.729A	кбит/с	мс	4
	G.728	кбит/с	2,5 мс	4
	G.726,G.727	кбит/с	0,125 мс	4
	G.711	кбит/с	0,125 мс	4

Источник	Стандарт	Скорость	Формат
Источник видеосообщения	H.261	64...384 кбит/с	QCIF(176x144) CIF(352x288)
Источник видеосообщения	H.262	64...1500 кбит/с	QCIF(176x144) CIF(352x288) 2CIF(352x576) 4CIF(704x576)
Источник видеосообщения	H.263	32...6000 кбит/с	SQCIF(128x96) QCIF(176x144) CIF(352x288) 2CIF(352x576) 4CIF(704x576) 16CIF(1408x1152)

Табл.1

Табл.2

Рис.3

2.Методы модуляции в спутниковых радиолиниях

2.1.Классификация

Рис.4

2.2.Принцип фазовой манипуляции (BPSK и QPSK)

                                Принцип BPSK                                               Принцип QPSK

Скорость передачи Rb (бит/с)= N (бит)/T (секунд)               Скорость передачи Rb (бит/с)= 2N (бит)/T (секунд)

Скорость манипуляции Rs (Бод)= N (симв)/T (секунд) Скорость манипуляции Rs (Бод)= N (симв)/T (секунд) 2.3.Комплексное представление модулированных сигналов

Синфазный сигнал в основной полосе частот                                     Представление модулированного сигнала комбинацией

                                    Синфазное плечо                                                                          квадратурных компонент

a t( ) = b_p (t)cos(ω_ct)+b_q (t)cos(ω_ct +π/2) =

⁺¹(1)

-1                                                                                          Модулированный                                 b tp ( )cos(ωct)−bq (t)sin(ωct)

радиосигнал

a t( )                                  Комплексный сигнал    b t( ) = bp (t)+ jbq ( )t                                                                  (2)

в основной полосе частот

Представление а(t) в виде произведения  комплексного сигнала в основной полосе частот

                                                                                        Мощность                                на комплексную синусоиду

+1

Квадратурный сигнал в основной полосе частот BPSK	Рис.7	p                    c            q                   c                                                c
		2.4.Фазовая диаграмма QPSK                              8-PSK	QAM-16

^-1S = (b_p² +b_q² )/2 ⁽⁴⁾                                    a t( ) = b (t)cos(ωt)−b (t)sin(ωt) = Re{b( )t exp( jωt)} (3)

                M=2k=1=2                                    k=k2                                           k=k3              k=4k

k                                                                 M=2 =4²                    Рис.8                M=2 =82       M=2 =16

2

Ps=1 =1                                     Ps=A                                          Ps=A           Ps=ia2, i=2,10,18

2.5.Частотная эффективность

Занимаемая полоса (при использовании
фильтрации Найквиста, без кодирования) G f( )	Занимаемая полоса

W_M = R_s (1+β) = R_b(1+β)/log₂ M

W_BPSK = R_s (1+β) = R_s = R_b = R_b(1+β)

W_QPSK = R_s (1+β) = R_s = R_b /2 = R_b(1+β)/2                                                                                                                                                        (5)

W_8−PSK = R_s (1+β) =R_s = R_b /3 = R_b(1+β)/3

W_{QAM −16} = R_s (1+β) = R_s = R_b /4 = R_b(1+β)/4

-1/(2T_s)       0        +1/(2T_s)           f

Занимаемая полоса  уменьшается пропорционально  фактору W = R_s (1+β β), = 0...1 сглаживания  (растет сложность фильтра)

β -фактор сглаживания (roll-off factor)

2.6.Энергетическая эффективность

Упрощенная модель спутниковой радиолинии

Искажения: тепловой шум, межсимвольная интерференция

Шум

Данные

T(f)                                                              R(f)                              Рис.10

Условия максимальной верности  приема

⎧T f( )×R( )f = RC( )f −критерий Найквиста                       Исключение межсимвольной интерференции

                (6) ⎨               _*

⎩T f( )= R ( )f                  −критерий согласованности фильтров        Снижение влияния теплового шума

RC( )f − raised cosine spectrum                                                                                              Практическая реализация:

                 Решение       (7)      R( f ) = T( f ) =    RC( f )

(фильтрНайквиста) root-raised cosine filter Комплексная модель шума  в основной полосе частота

1  ⎛ n² ⎞

Функция плотности p n( ) = exp_⎜− 2 _⎟ (8) вероятности _{__} σ π² _⎝ 2^σ ⎠

2  2

Мощность шума               ^P_n ^{= n =σ}                                (9)

Модель

Спектральное представление n t( ) = A(t)cos[ω_ct +ϕ(t)]= n_p(t)cos(ω_ct)−n_q( )t sin(ω_ct)(10) ⁿ_p,ⁿ_q -независимые СВ с гаус. распр.вер.

_______         _______

n2p ( )t = nq2 ( )t =σ2 = Pn (11)                                        No

эквивалентно

A         ⎛     A² ⎞

                     Рис.11p A( ) = ₂ exp⎜−                  ₂ ⎟      (12)

σ ⎝ 2σ ⎠                                                                   Рис.12

ϕ -равномерно распределенная СВ

Обобщенная схема оптимального демодулятора Принцип анализа помехоустойчивости (BPSK)

⎞

⎟

Помехоустойчивость (при использовании фильтрации Найквиста, без кодирования) - теоретический предел для данных видов модуляции

⎞

o ⎠

Рис.15

2        4        6        8       10      12      14 16

E_b / N_o ,дБ

2.7.Практическая реализация модулятора и демодулятора BPSK

Модулятор                                                              Демодулятор

Рис.16

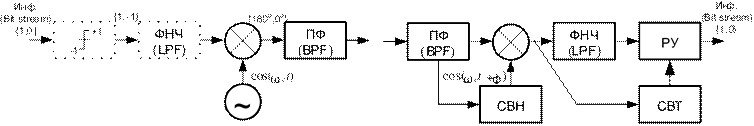
2.8.Практическая реализация модулятора и демодулятора QPSK

Модулятор

Демодулятор

3.Помехоустойчивое кодирование в спутниковой связи

3.1.Разновидности  кодирования

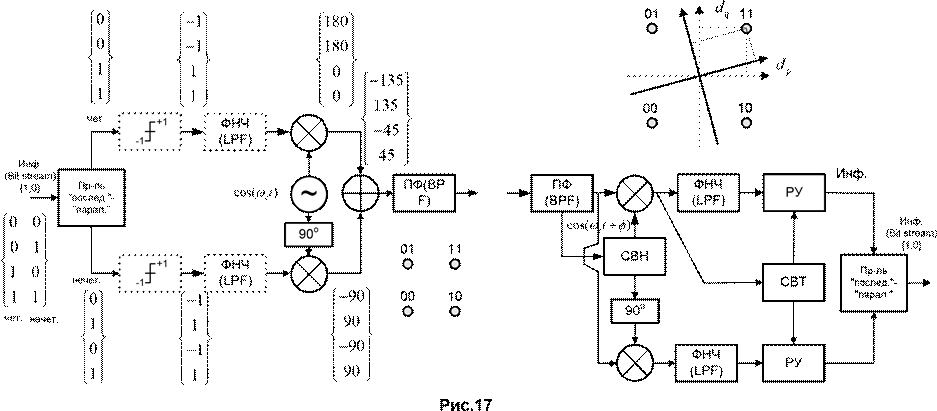
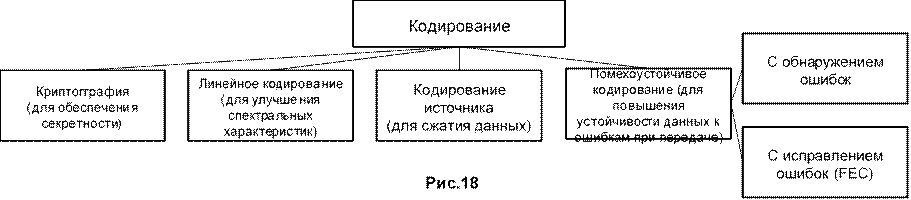
3.2.Введение в помехоустойчивое кодирование c исправлением ошибок (FEC)

Цель - повышение энергетической эффективности.                      Шеннон: в любом канале можно передавать

Эффект выражается выигрышем от кодировани                        информацию со скоростью, равной пропускной способности данного канала, со сколь угодно малыми ошибками, используя соответствующее кодирование

Выигрыш                         Принципы: структурирование и избыточность

от кодирования

Инф. биты	Провер. биты
00	000
01	110
10	011
11	101

01

110

00	000
10	011

11

101

Избыточность: из 32 комбинаций использовали только 4

Eb/No,дБ

Структурирование: выбрали максимально

удаленные друг от друга комбинации

Цифрами указано расстояние Хэмминга.

В центре – принятое с одной ошибкой  к.слово.

Выбирается ближайшее к.слово.

Рис.19

Расстояние Хэмминга: 00000 и 10011 различаются  в трех позициях, т.е. РХ=3

Рис.20

Цель - повышение энергетической эффективности

Положительный результат - достижение требуемой  достоверности передачи при меньших энергетческих затратах

Негативные стороны: расширение занимаемой полосы; увеличение задержки обработки; усложнение и удорожание аппаратуры

Рис.21

3.3.Сверточное кодирование

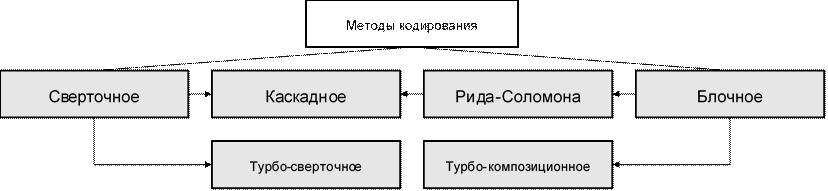
Сверточное кодирование заключается в выполнении операции свертки входной последовательности и импульсной характеристики (реакции на единичное импульсное воздействие)  кодера.

Процесс кодирования осуществляется непрерывно во времени. Не требуется блоковая синхронизация.

Пример кодера:  код (7,5)                                          Процесс кодирования: решетчатая диаграмма

кол.комбинаций= 1/2

Состояния                 Шаг кодирования

Длина кодового ограничения v=3 Свободное расстояние df=5 Рис.22

передать посл. 10000…): 1+D2, 1+D+D2, т.е.  (5, 7) в восьмеричной форме

Рис.23 Замечания: а)число состояний =2v-1 = 23-1= 4 а)состояния кодера изменяются  в пределах разрешенных; б)на любом шаге кодирования движение от одного и того же состояния  при одинаковых входных данных будет сопровождаться формированием одинаковых кодовых последовательностей;

Декодирование сверточных кодов     в)свободное расстояние dfree=5 (штриховая линия).

Пример алгоритма Витерби (метрика Хэмминга)

Передано

11            01             01            00              10 11

Ошибка

                                                                                                                                     0           1          2           3           4           5 6

Состояния        Шаг кодирования

Исправленная последовательность

Рис.25                                                    Рис.26          11            01             01           00                                                     10                                                                                                    11

Получение более высоких скоростей кодирования: выкалывание

Получение скорости 2/3: отбразывание первого кодового символа через период кодирования

Входная последовательность бит

Эффект:

а)увеличение кодовой скорости дает уменьшение занимаемой полосы