Пиковое, среднеквадратическое, средневыпрямительное и среднее значение напряжений сигнала

Министерство РФ информационных технологий и связи

СибГУТИ

Кафедра ПДС и М

Индивидуальное задание № 2

Вариант № 56

                                                                            Выполнил:

А-33

                                                Проверил: И

Новосибирск

2005 г.

Условия задачи, [1], стр. 7

Для исходных данных, в соответствии с номером варианта, решить следующие задачи:

1. Найти пиковое, среднеквадратическое, средневыпрямительное и среднее значение напряжений сигнала.
2. Найти коэффициенты амплитуды и формы сигнала.
3. Отыскать показания вольтметров, которые проградуированы в среднеквадратических значениях для синусоидального сигнала:

a)  Среднеквадратического с открытым входом;

b)  Средневыпрямленного значения с открытым входом;

c)  Пикового значения с открытым входом;

d)  Пикового значения с закрытым входом;

4. Показания пиковых вольтметров с закрытым и открытым входом, которые проградуированы в пиковых значениях.
5. Оценить относительную погрешность показаний различных вольтметров, определенных в п.4.
6. Разработать методику экспериментального определения значений коэффициентов амплитуды и формы.

Таблица 1. Исходные данные к заданию.

Первая цифра номера варианта Um, B Uk, B Класс точности Вторая цифра номера варианта Форма сигнала Период сигнала Т, мс Длительность импульса τ, мс

5 300 300 2 6 е 0,5 0,5

U_k – конечное значение шкалы вольтметра.

     U(t)

U_m

 

τ/2         τ                                             t

Т

 

Рисунок 1. Форма сигнала к заданию.

Сигнал заданной формы описывается уравнением

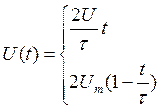
, 0≤t≤τ/2

, τ/2≤t≤T

1. Найдем:

а) пиковое значение напряжений сигнала, т.е. наибольшее или наименьшее значения сигнала U(t) на интервале измерения:

U_m= max{U(t)}  [1], стр. 85, где мах – операция нахождения максимального(минимального) значения сигнала на интервале измерения Т.

В нашем случае сигнал принимает 2 пиковых значения: пиковое вверх U_m и пиковое вниз, равное нулю.

U_m=300 B

б) среднеквадратическое значение за время измерения определяется выражением:

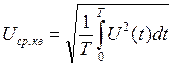   [1], стр. 86

Для нашего случая:

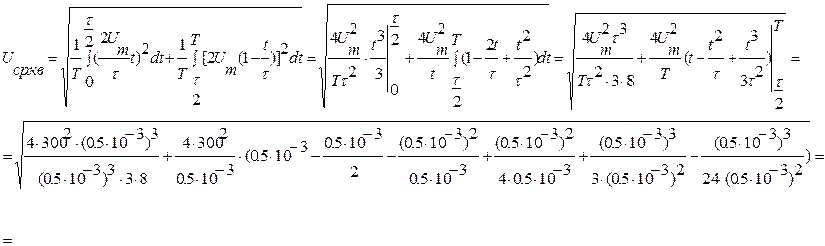
171,75564

в) средневыпрямленное значение за время измерения можно найти из выражения:

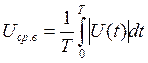  [1], стр. 86

Геометрически это сумма площадей, ограниченная кривая над и под осью времени за время измерения Т.

При однополярном напряжении в нашем случае:

U_ср.в = U_ср  [1], стр. 86

U_ср.в = 150 В (см. ниже)

г) среднее значение за время измерения определяется выражением:

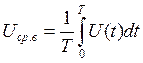 [1], стр. 85

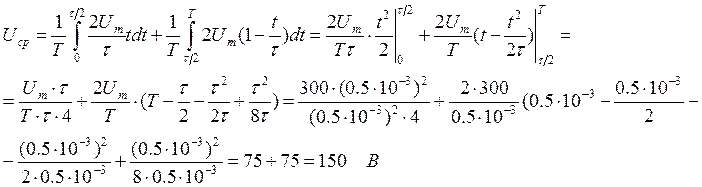
2. Найдем коэффициенты амплитуды и формы сигнала.

Коэффициент амплитуды определяется выражением

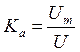   [1], стр. 86, где U_m – пиковое значение напряжения,

U – среднеквадратическое

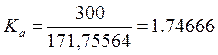
Коэффициент формы определяется выражением:

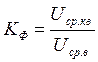  [1], стр. 86

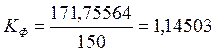
Проверим выполнение неравенства для полученных коэффициентов:

1≤K_ф≤K_а≤K_у   [1], стр. 86,

Где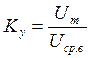     

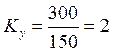
1≤1.14503≤1.74666≤2

Неравенство выполняется.

3. Определяется показания вольтметров которые проградуированы в среднеквадратических значениях для синусоидального сигнала. а) среднеквадратического с открытым входом

Показания вольтметра определяются формулой:

А_n = C∙U   [1], стр. 89, где С – градуировочный коэффициент

А_n = С∙U_ср.кв

С = 1              [1], стр. 89

А_n = 171,75564 B

б) средневыпрямленного значения с открытым входом:

А_n = С∙U_ср.в    [1], стр. 89

C = 1,11         [1], стр. 89

А_n = 1,11∙150 = 166,5 B

в) пикового значения с открытым входом.

А_n = С∙U_m      [1], стр. 89

С = 0,707       [1], стр. 89

А_n = 0,707∙300 = 212,1 В

г) пиковое значение с закрытым входом:

при закрытом входе вольтметр измеряет только переменную составляющую сигнала.

A_n = C(U_m – U_ср.в.)   [1], стр. 91

С = 0,707                  [1], стр. 89

А_n = 0,707(300-150)=106,05  В

4. Определим показания пиковых вольтметров с закрытым и открытым входом, которые проградуированы в пиковых значениях.

A_n.отк. = С∙U_m    

C = 1             [1], стр. 91

A_n.отк. = 1∙300 = 300  B

A_n.закр.= С(U_m-U_ср)    [1], стр. 91

A_n.закр.= 1∙(300-150) = 150  В

5. Оценим относительную погрешность показаний различных вольтметров, определенных в п.п. 3,4.

Δ_пред = γ/100∙А_норм         [3], стр. 9, где Δ_пред – предел допускаемой абсолютной погрешности.

γ – класс точности;

А_норм – нормированное значение

δ_пред = Δ_пред/А_n∙100%      [2], стр. 7,

δ_пред – предел допускаемой относительной погрешности;

A_n – показания вольтметрах

А_норм = А_kmax = U_k           [3], стр. 9

А_норм = 300  В

тогда              Δ_пред = 2/100∙300 = 6  В

Рассчитаем погрешность для пункта 3:

а)         δ_пред = 6/171,75564 ∙ 100% = 3,49333% ≈ 3,5%

Погрешность округления ([3], стр. 4):

δ_окр = (3,5-3,49333)/ 3,49333 ∙ 100% = 0,2%   <  5%

б)        δ = 6/166,5∙100% = 3,60360 ≈ 3,7

δ_окр = (3,7-3,60360)/ 3,60360 ∙ 100% = 2,7%   <  5%

в)         δ = 6/212,1∙100% = 2,82886 ≈ 2,9%

δ_окр = (2,9-2,82886)/ 2,82886 ∙ 100% = 2,5%   <  5%

г)         δ = 6/106,05∙100% = 5,65771% ≈ 5,7%

δ_окр = (5,7-5,65771)/ 5,65771 ∙ 100% = 0,75%   <  5%

Аналогично для пункта 4:

δ_отк  = 6/300∙100% = 2,0 %

δ_закр = 6/150∙100% = 4,0 %

6. Разработаем методику экспериментального определения значения коэффициентов амплитуды и формы.

 

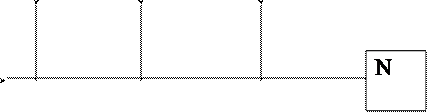
Рисунок 2. Схема определения пикового среднеквадратического и средневыпрямленного значения сигнала.

Измерение значений коэффициентов амплитуды и формы сигнала можно осуществить косвенным методом, согласно выражениям:

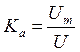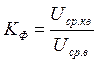  ;       [1], стр. 86

Измерение значений U_m, U_ср.кв, U_ср сигнала произвольной формы возможно только вольтметром с адекватным преобразователем.

Отметим, что на схеме (рисунок 2):

а) все вольтметры проградуированы в среднеквадратических знавениях синусоидального сигнала;

б) тип входа вольтметров – открытый;

в) вольтметр V₁ имеет преобразователь среднеквадратических значений, V₂ – средневыпрямленных значений, V₃ – пиковый преобразователь.

Также для эксперимента необходим генератор сигналов произвольной