Симметричный кабель в свинцовой оболочке с кордельно-стирофлексной изоляцией. Расчет первичных и вторичных параметров передачи

ФЕДЕРАЛЬНОЕ АГЕНСТВО СВЯЗИ

Кафедра ЛС

Расчетно-графическое задание

ПО КУРСУ НЭС

вариант № 25

Выполнила:Студентка 3 курса

                                                                            группы А-45 

                                                                                               

Проверила:ст.пр.      

Новосибирск

2006

          Задание: Рассчитать первичные (R[Ом/км]; L[Гн/км]; C[Ф/км]; G[См/км]) и вторичные (α[дБ/км]; β[рад/км]; V[км/с]; Zв[Ом]) параметры передачи, кабеля МКСБ –  в заданном диапазоне частот f: 32кГц – 150кГц – 252кГц. По Результатам расчётов построить графики частотных зависимостей и сделать выводы.

          Решение: По условия задачи нам задан кабель МКСБ – . МКСБ:  симметричный кабель в свинцовой оболочке с кордельно-стирофлексной  изоляцией, заключённый в бронь из двух стальных лент с наружным покровом.  означает что в кабеле присутствуют 4 звёздные скрутки, диаметр медной жилы 1,2 мм.

Определим диаметр изолированной жилы  по формуле:

– диаметр токопроводящей жилы
–  толщина изолирующей ленты
– диаметр корделя
n – число лент	n=1

Расстояние между центрами проводников а:

Диаметр звёздной скрутки :

Коэффициент укрути  равен: .

Сопротивление дополнительных потерь  определяется из таблицы 1,2 [1, стр.17]: .

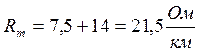Удельное сопротивление меди(Cu):  .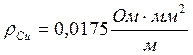

Сопротивление проводника на постоянном токе: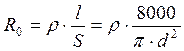

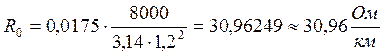
Поправляющий коэффициент p учитывающий структуры жил в кабеле для звездной скрутки: .

Радиус проводника : .

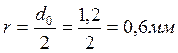Поправочный коэффициент  характеризует близость проводников к заземлённой оболочке и другим проводникам, равен: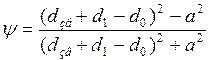

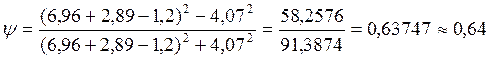
Расчёт для частоты .

Для нахождения функции Бесселя необходимо вычислить значение kr:

Значения специальных функций Бесселя F(kr), G(kr), H(kr), Q(kr) определяем по таблице из методических указаний [1,стр.19], при этом используем метод экстраполяции.

В результате получаем:

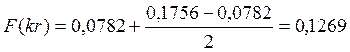
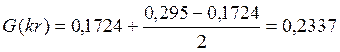
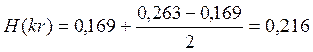
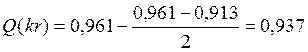
Дополнительное сопротивление R_M, обусловленное влиянием вихревых токов в проводах смежных четверок, определим как:

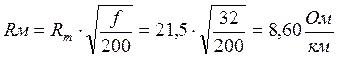
Для вычисления активного сопротивления кабельной цепи воспользуемся формулой:

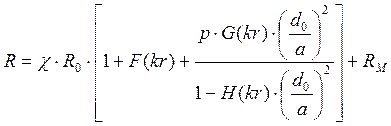, Ом/км, где

R0 – сопротивление постоянному току, Ом/км;

Rм – сопротивление, обусловленное потерями на вихревые токи в соседних металлических элементах, Ом/км;

χ – коэффициент укрутки;

a – расстояние между центрами проводников, мм;

d₀ – диаметр токопроводящей жилы, мм;

p – коэффициент, учитывающий вид скрутки (при звездной р=5);

F(kr), G(kr), H(kr) – специальные функции Бесселя.

Подставим численные значения:

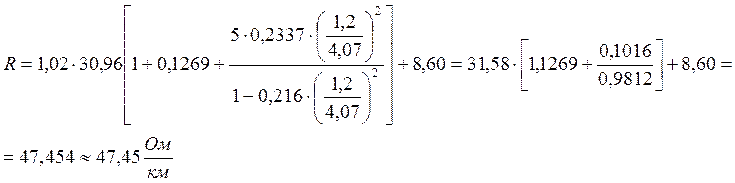
Вычислим значение индуктивности  цепи:

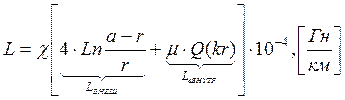, где

χ – коэффициент укрутки;

a – расстояние между центрами проводников, мм;

r – радиус голого проводника, мм;

µ – относительная магнитная проницаемость;

Q(kr) – специальная функция Бесселя.

Подставим численные значения:

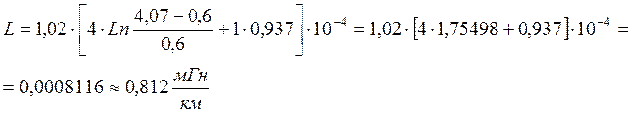
Вычисление величины ёмкости С произведем по формуле:

,

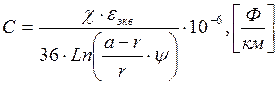где

χ – коэффициент укрутки;

a – расстояние между центрами проводников, мм;

r – радиус голого проводника, мм;

Ψ – поправочный коэффициент, характеризующий близость металлических элементов;

εэкв – относительная диэлектрическая проницаемость.

Подставим численные значения:

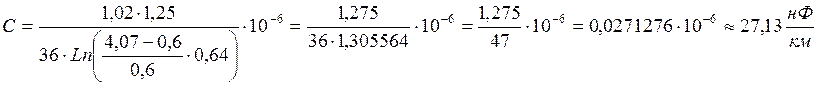
Тангенс диэлектрических потерь  берём из таблицы 1,8 [1, стр.22]:

Проводимость изоляции G характеризует потери энергии в изоляции проводов кабеля и обусловлена сопротивлением изоляции изолирующего материала диэлектрических потерь. В общем виде формула имеет вид:

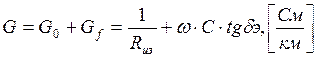, где

G₀ – проводимость изоляции по постоянному току, См/км;

G_f – проводимость изоляции по переменному току, См/км;

Rиз – сопротивление изоляции кабельной цепи;

ω – круговая частота (ω=2πf);

C – емкость симметричной цепи;

– тангенс угла диэлектрических потерь.

Так как сопротивление изоляции бесконечно большое, поэтому 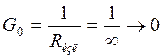 и проводимость изоляции  найдем  как:

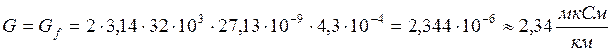
Волновое сопротивление цепи  вычисляют по формуле:

.

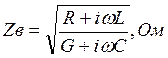Но в области высоких частот (при f>30кГц) волновое сопротивление цепи  определяется по формуле:

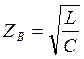,Ом, где

L – индуктивность цепи, Гн/км;

C – емкость цепи, Ф/км.

Подставим численные значения:

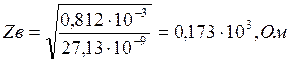
Вычислим коэффициент затухание  в кабельной симметричной цепи по формуле:

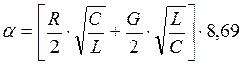, дБ/км, где

G – проводимость изоляции цепи, См/км;

R – сопротивление цепи, Ом/км;

L – индуктивность цепи, Гн/км;

C – емкость цепи, Ф/км.

Подставим численные значения:

.

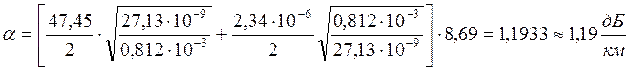
Коэффициента фазы  определяет угол сдвига между током (напряжением) на протяжении одного километра, определим его по формуле:

, рад/км, где

ω – круговая частота (ω=2πf);

L – индуктивность цепи, Гн/км;

C – емкость цепи, Ф/км.

Подставим численные значения:

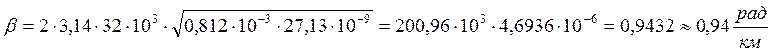
Скорость распространения электромагнитной энергии является функцией частоты и фазовой постоянной, которая в свою очередь зависит от первичных параметров линии. В общем виде она определяется по формуле:

.

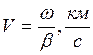В области высоких частот (при f>30кГц), когда скорость не зависит от частоты и определяется только параметрами кабеля:

.

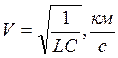Подставим численные значения:

.

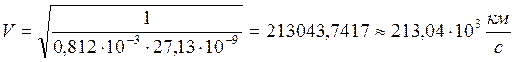Расчёт для частоты .

Для нахождения функции Бесселя необходимо вычислить значение kr:

Значения специальных функций Бесселя F(kr), G(kr), H(kr), Q(kr) определяем по таблице из методических указаний [1,стр.19], при этом используем метод экстраполяции.

В результате получаем:

Дополнительное сопротивление R_M, обусловленное влиянием вихревых токов в проводах смежных четверок, определим как:

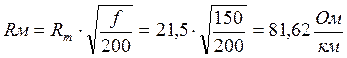
Для вычисления активного сопротивления кабельной цепи воспользуемся формулой:

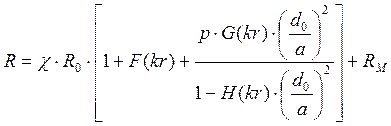, Ом/км, где

R0 – сопротивление постоянному току, Ом/км;

Rм – сопротивление, обусловленное потерями на вихревые токи в соседних металлических элементах, Ом/км;

χ – коэффициент укрутки;

a – расстояние между центрами проводников, мм;

d₀ – диаметр токопроводящей жилы, мм;

p – коэффициент, учитывающий вид скрутки (при звездной р=5);

F(kr), G(kr), H(kr) – специальные функции Бесселя.

Подставим численные значения:

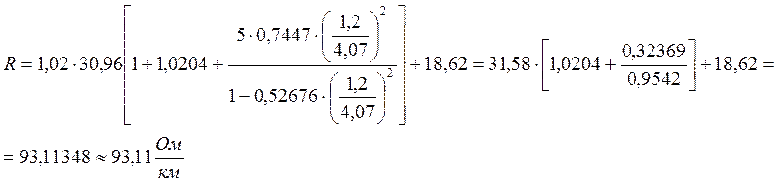
Вычислим значение индуктивности  цепи:

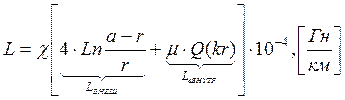, где

χ – коэффициент укрутки;

a – расстояние между центрами проводников, мм;

r – радиус голого проводника, мм;

µ – относительная магнитная проницаемость;

Q(kr) – специальная функция Бесселя.

Подставим численные значения:

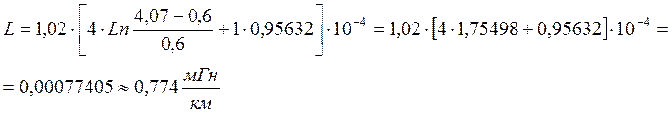
Вычисление величины ёмкости С произведем по формуле:

,

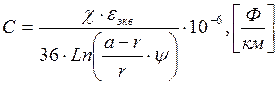где

χ – коэффициент укрутки;

a – расстояние между центрами проводников, мм;

r – радиус голого проводника, мм;

Ψ – поправочный коэффициент, характеризующий близость металлических элементов;

εэкв – относительная диэлектрическая проницаемость.

Подставим численные значения:

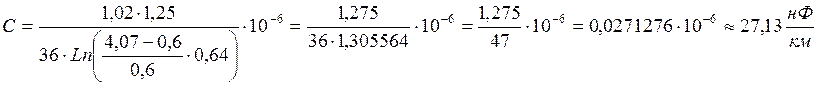
Тангенс диэлектрических потерь  берём из таблицы 1,8 [1, стр.22]:

Проводимость изоляции G характеризует потери энергии в изоляции проводов кабеля и обусловлена сопротивлением изоляции изолирующего материала диэлектрических потерь. В общем виде формула имеет вид:

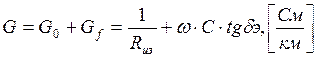, где

G₀ – проводимость изоляции по постоянному току, См/км;

G_f – проводимость изоляции по переменному току, См/км;

Rиз – сопротивление изоляции кабельной цепи;

ω – круговая частота (ω=2πf);

C – емкость симметричной цепи;

– тангенс угла диэлектрических потерь.

Так как сопротивление изоляции бесконечно большое, поэтому 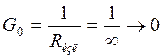 и проводимость изоляции  найдем  как:

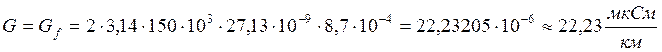
Волновое сопротивление цепи  вычисляют по формуле:

.

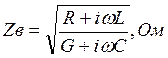Но в области высоких частот (при f>30кГц) волновое сопротивление цепи