Расчет системы технико–экономических показателей (ТЭП) по совокупности предприятий (30 мебельных предприятий), страница 6

По качественным показателям групповые и общие средние величины нужно определять только по данным карточек, исходя из сущности усредняемого показателя, то есть знания того, соотношением каких величин этот показатель исчисляется.

Перестроенная комбинационная таблица позволяет проследить на конкретных цифрах – в абсолютном и относительном выражении, какова зависимость между экономическими показателями.

Для большей наглядности необходимо построить эмпирический график зависимости результативного признака (z) от факторного (х), то есть в системе координат нанести фактическую линию регрессии между ними. График строится на основе групповых средних величин, исчисленных по первичным данным, то есть по карточкам. При этом на оси абсцисс наносятся сведения по факторному признаку, а на оси ординат - по результативному. Количество точек на графике соответствует числу групп, образованных по факторному признаку.

Ломаная линия, соединяющая эти точки, дает представление о направлении  и характере связи. Для большей наглядности тесноты связи рекомендуется по данным карточек нанести на график все 30 значений - пар связей, характеризующих собой "облако рассеяния".

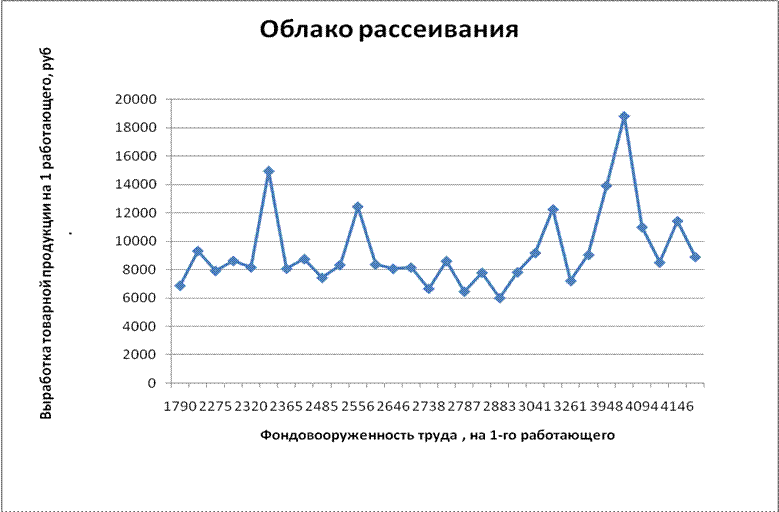
1.4. Применение графического способа для выявления формы связи между показателями и расчет корреляционного уравнения зависимости (уравнения регрессии – y=f(x)).

1. На основе фактической линии регрессии, представленной на графике зависимости в виде ломаной линии выбрать форму связи между факторными и результативными признаками.

2. По данным перестроенной комбинационной таблицы рассчитать теоретическое уравнение корреляционной зависимости, используя выбранную форму связи: уравнение прямой, гиперболы, параболы, показательной функции.

3. Теоретическое значение () нанести на график и провести теоретическую линию регрессии.

Исходя из графика, характеризующего собой фактическую линию регрессии, выберем прямую форму связи между факторными и результативными признаками.

Экономические показатели находятся между собой в корреляционной зависимости. Метод корреляции базируется на законе больших или средних чисел. Исходя из этого закона, корреляционной зависимости придается математическая форма связи, определяемая методом наименьших квадратов. Параметры корреляционного уравнения связи (свободный член и коэффициенты регрессии) находятся путем решения систем нормальных уравнений.

Для уравнения прямой система нормальных уравнений выглядит так:

где х — факторный признак; у — результативный признак, (численные значения по этим признакам берутся из перестроенной комбинационной таблицы - это средние групповые, исчисленные по данным карточек); у_х - теоретические значения результативного признака, исчисленные после решения системы нормальных уравнений и нахождения параметров "а" и "Ь" и подстановки фактических значений факторного признака; п - число групп факторного признака, совпадающее с количеством групповых средних.