Формулы для определения потенциалов каждой строки или столбца матрицы. Улучшение опорного плана

Формулы для определения потенциалов каждой строки или столбца матрицы:

V_j=U_i+C_ij ;                                                     (12)

U_i=V_j-C_ij ;                                                      (13)

Назначается начальный потенциал. Он должен быть больше, чем наибольшая единичная стоимость. Это необходимо, чтобы исключить возможность отрицательных значений потенциалов.

Принимаем U_i =

Все расчеты сведены в таблицу 12.

Таблица 12.

I	J	1	2	3	4	5	6	Ui
	Bi Ai
Vj

Для каждой незаполненной клетки подсчитывается разность:

∆=V_i+U_i-C_ij<0

∆₁₁=

∆₁₂=

∆₁₃=

∆₁₄=

∆₂₂=

∆₂₃=

∆₂₅=

∆₃₁=

∆₃₄=

∆₃₅=

∆₃₆=

∆₄₁=

∆₄₃=

∆₄₄=

∆₄₆=

∆₅₃=

∆₅₄=

∆₅₅=

∆₅₆=

Проверка  показала, что  план  не  является оптимальным, так как разность ∆ в клетках

2-3, 3-6, 5-3, 5-4 положительна. Максимальное нарушение условия оптимальности в клетке 5-3, ∆₅₃=0,09.

Следовательно план необходимо скорректировать.

Улучшение опорного плана.

Для улучшения распределения поставок в базисном плане перевозок находится клетка с максимальным нарушением условия оптимальности и для нее строится замкнутый контур или цикл перераспределения.

Цикл перераспределения представляет собой замкнутый многоугольник (прямоугольник), опирающийся вершинами на заполненные клетки матрицы, кроме одной вершины, которая должна располагаться в незаполненной клетке с максимальным нарушением условия оптимальности.

Если выполняется условие m+n-1≤10, то для каждой незаполненной клетки матрицы можно построить единственный цикл перераспределения.

Клетки многоугольника перераспределения делятся на загруженные и разгружаемые.  Клетка с наибольшим нарушением условия оптимальности является загружаемой. Суммарное количество разгружаемых клеток равно количеству загружаемых клеток.

Максимальная величина поставки в клетку с наибольшим нарушением условия оптимальности равна минимальной величине поставки из разгружаемых клеток.

3-2                                           3-3 

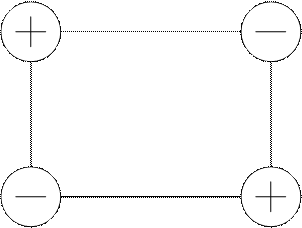
40+40=80 40-40=0                                                    

40-40=0              0+40=40

5-2                                           5-3

Таблица 13.

I	J	1	2	3	4	5	6	Ui
	Bi Ai
Vj

В матрице зачеркиваем старые величины поставок и записываем новые. Дальнейшие расчеты повторяют вышеизложеное.

∆₁₁=

∆₁₂=

∆₁₃=

∆₁₄=

∆₂₂=

∆₂₃=

∆₂₅=

∆₃₁=

∆₃₄=

∆₃₅=

∆₃₆=

∆₄₁=

∆₄₃=

∆₄₄=

∆₄₆=

∆₅₃=

∆₅₄=

∆₅₅=

∆₅₆=

Проверка показала, что нарушение оптимальности имеется в следующих клетках:

3-6 и 5-4.  Максимальное нарушение условия оптимальности в клетке 3-6 ∆₃₆=0,05.

План не является оптимальным, поэтому его необходимо скорректировать.

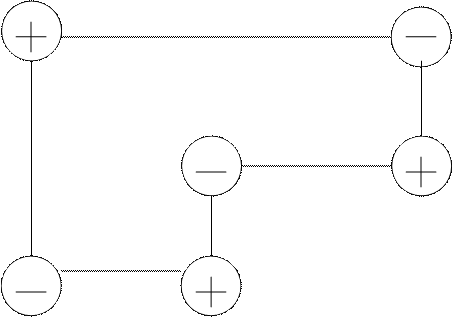
2-1  2-6

60+40=100                                                                                           40-40=0

3-2                                  

80-40=40                                                       0+40=40

3-6

140-40=100                                                  0+40=40

5-1                              5-2           

Таблица 14.              

I	J	1	2	3	4	5	6	Ui
	Bi Ai
Vj