Предельная толщина масляного слоя зависит от скорости скольжения.
При малых скоростях скольжения она меньше, чем при больших. Без учета перекоса или с малым перекосом при υ = 0,5 м / с hlim = 8 мкм, при υ = 0,2 м / с hlim = 6 мкм, при совсем малой скорости hlim = 3 мкм.
Скорость цапфы найдем по формуле
υ = ω d / 2 = 163,28 · 0,065 / 2 = 5,3 м /с > 0,5 м / с.
Принимаем hlim = 8 мкм.
Найдем относительный эксцентриситет χ = (Δ - 2 hlim) / Δ.
Так как Δ = 102 мкм, то χ = (102 – 2 · 8) / 102 = 0,843.
Для вычисления коэффициента нагруженности СR найдем значение m в зависимости от l / d = 50 / 65 = 0,77, где l и d – соответственно длина и диаметр шатунной шейки m = 0,758.
Отсюда СR = m / (1 – χ) – m = 0,758 / (1 – 0,843) – 0,758 = 4,07.
Теперь найдем несущую способность подшипника:
F = 0,107 СRnld3η / Δ2 = 0,107 · 4,07 · 1560 · 66 · 653 · 0,04 / 1022 = 47,34кН.
Допуск для Ø40H7 δВ = 30 мкм, для Ø40е8 δс = 46 мкм, откуда найдем допуск на диаметральный зазор: δΔ= 1,1(δВ2 + δY2)1/2 = 1,1(302 + 462)1/2 = 57 мкм.
Принимая m = 0,758, находим частные производные функции F по Δ и η, вычисленные при средних значениях параметров:
(F)`Δ = 0,107nld3mη (2 / Δ3 – 1 / (2 Δ2hlim)) = 0,107 ·1560 · 66 · 653 · 0,758 · 0,04 · (2 / 1023 – 1 / 2 · 1022 ·8)) = - 378,2;
(F)`η = 0,107 nld3m / Δ2(Δ / (2hlim) – 1) = 0,107 · 1560 · 66 · 653 · 0,758 / (1022 · (102 / 2 · 8) – 1) = 1184786.
Среднее квадратическое отклонение несущей способности подшипника вычисляют по формуле
S = 1/6 ([(F)`Δ δΔ]2 + [(F)`η δη]2)1/2 = 1/6 ([378,2 · 57]2 + [1184786 х х 0,013]2)1/2 = 4416Н = 4,4кН.
Используя полученные значения радиальной нагрузки Fr = 4,4 кН, несущей способности подшипника F = 47,34 кН и среднего среднего квадратического отклонения SF = 4,4 кН, найдем квантиль нормального распределения Zp, определяющий вероятность безотказной работы:
Zp = (Fr – F) / SF = 4,4 – 47,43 / 4,4 = - 9,73.
Отсюда следует, что вероятность безотказной работы больше 0,999999, то есть вероятность отказа Р(q) < 10-6.
По нагрузке на подшипник Fr = 4,4 кН и несущей способности F = 47,34 кН получаем коэффициент запаса nF = 47,34 / 4,4 = 10,86.
Таким образом, коленчатый вал по принятому критерию износостойкости практически абсолютно надежен.
5.2.2. Вероятностный расчет износа сопряжения вал – вкладыша
Как было указано выше, отказ подшипника скольжения может быть вызван повышенным износом вала и вкладыша. Для нашего можно допустить, что скорость изнашивания линейно зависит от давления и скорости: g1 = k1pu;
g2 = k2pu, где g1, g2 – скорости изнашивания вала и вкладыша соответственно;
k1 ,k2 – коэффициенты износа, характеризующие материалы пары и условия работы, для вала и вкладыша соответственно; u - окружная скорость вала. Для стального вала и вкладыша из антифрикционной бронз примем
k1 = 1 · 10-13 МПа-1; k2 = 3 · 10-13 МПа-1.
Скорость износа сопряжения
g1-2 = 2pk2A0n / (l0 (0,5sin 2a0 + a0 – k1sina0 / (pk2 + a0k1))), где l0 – длина шейки (ширина подшипника), мм;
A0 – опорная реакция, Н; А0 = 4400 Н.
n – частота вращения вала, час-1; n = 93600 час-1;
a0 = p / 2.
Подставляя все известные величины находим
g1-2 = 2p · 3 · 10-13 · 4400 · 93600 / ( 0,066 ( 0,5 · 0 + p / 2 – 1 · 10-13 / (p · 3 · 10-13 + p / 2 · 10-13))) = 7,87 · 10-3 мкм / ч.
Полученное
значение g1-2 примем как среднее и, задавшись
коэффициентом вариации в пределах 0,3…0,4, получим 
=
7,87 · 10-3 мкм / ч;
Sg1-2 = ug =
0,3 · 7,87 · 10-3 = 2,361 · 10-3 мкм / ч.
Для нахождения вероятности отказа воспользуемся моделью формирования постепенного отказа с учетом рассеивания начальных параметров изделия:
Р (t) = 0,5 – Ф [(Xmax - 
-
g t ) / (Sa02 + Sg2 t2)1/2)], где Xmax – величина максимально допустимого зазора между шатунной шейкой вала и
вкладышем;
– среднее значение начального
параметра, в качестве которого берем величину зазора перед началом эксплуатации;
Sa0 – среднее квадратическое отклонение начального парметра;
t – отрезок времени.
Для
определения значений Xmax, и Sa0 построим поля допусков принятой нами посадки Ø65H7/е8
Xmax = amax = δВ + δУ + amin = 30 +46 +60 = 136 мкм;
= amin + δВ / 2 + δУ / 2 = 60 + 30 / 2 + 46 / 2 = 96 мкм.
Предположив, что величина зазора подчиняется нормальному распределению, среднее квадратическое отклонение Sa0 можно оценить как 1/6 от величины аmax - аmin:
Sa0 = 1/6 (amax - amin) = 1/6 (136 - 98)= 6,33 мкм.
Величину t определим как время, за которое коленчатый вал испытывает базовое число циклов нагружения, в данном случае NБ = 5 · 105 циклов. Так как известна частота вращения n, то t = NБ / n = 5 · 105 / 93600 = 53,42 ч. Подставим полученные данные и найдем
P (t) = 0,5 – Ф = [ (136 – 98 – 7,87 · 10-3 · 53,42) / (6,332 + (2,36 · 10-3)2 · 53,422)1/2] = 0,5 – Ф [5,94] = 0,5 – [0,999999 / 2] = 5 ∙ 10-7.
Полученный результат говорит о том, что за расчетное время наработки t ≈ 54 ч из 100 тыс. эксплуатируемых коленчатых валов выйдет из строя не более одного из – за недопустимости износа.
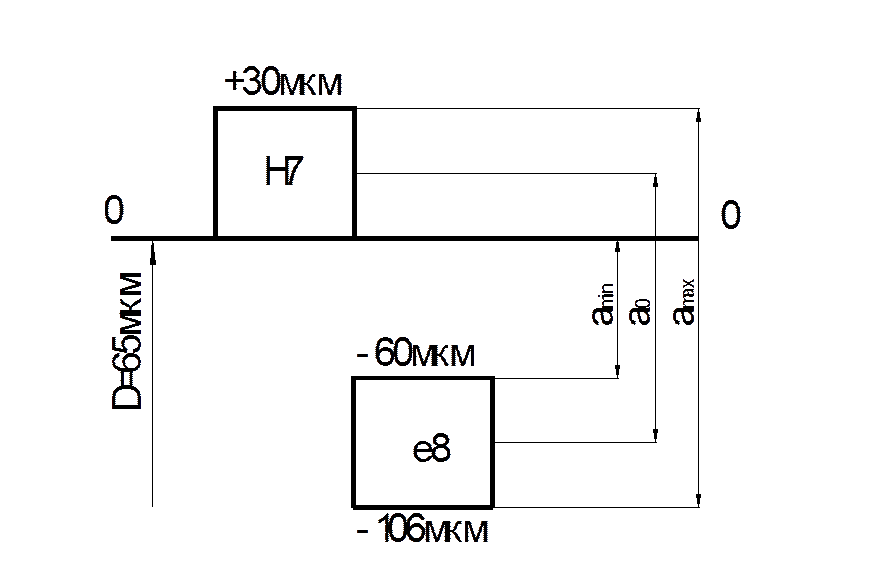
Рис 5.2 - Схема поля допуска для посадки Ø65H7/е8
6 Анализ результатов расчета
Полученные расчетные данные сведем в таблицу. Из нее следует, что за установленное время эксплуатации ожидается:
- не более пяти отказов из 100000 валов по критериям износостойкости;
- не более семи отказов из 1000 валов по критериям сопротивления
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.