Исследование возникновения внеполосных излучений
По ГОСТ 23611-79 под внеполосным излучением понимается излучение в полосе частот, примыкающей к необходимой полосе частот, являющееся результатом модуляции сигнала. Это излучение является нежелательным, поэтому целесообразно создавать такие сигналы или способы модуляции, которые снижали бы его уровень. В то же время, сформировать излучение, полностью свободное от внеполосных составляющих, невозможно. Для уменьшения интенсивности внеполосных колебаний необходимо получить максимально большую скорость спадания огибающей спектра при увеличении расстройки по частоте за пределами необходимой полосы. Большинство сигналов в радиосвязи и локации имеют несущую частоту, значительно превышающую максимальную частоту модуляции. Для оценки спектра такого сигнала достаточно оценить лишь спектр его модулирующей функции. Для идеального прямоугольного импульса длительностью τ с несущей частотой ω0 спектр совпадает со спектром видеоимпульса, но сдвинут по частоте на величину ω0. Он описывается выражением
![]()
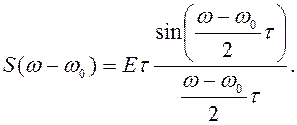 (1)
(1)
Заменив в выражении разность частот на Ω, т.е. перейдя к значению расстройки относительно несущей, выражение для спектра можно записать более компактно
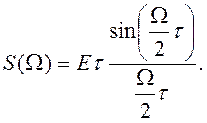 (2)
(2)
 Для решения задач, связанных с ЭМС интересен не сам
спектр, а его огибающая. Она определяется из выражения (2) заменой функции sin(Ωτ/2)
ее максимальным значением, равным 1. Тогда
Для решения задач, связанных с ЭМС интересен не сам
спектр, а его огибающая. Она определяется из выражения (2) заменой функции sin(Ωτ/2)
ее максимальным значением, равным 1. Тогда
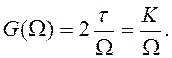 (3)
(3)
где К – константа.
Оценим скорость спадания огибающей спектра. Ее принято характеризовать дБ/декаду или в дБ/октаву. Если огибающая спектра спадает как К/Ωn , то скорость ее спадания в дБ/декаду определяется выражением
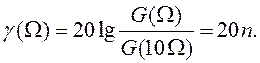 (4)
(4)
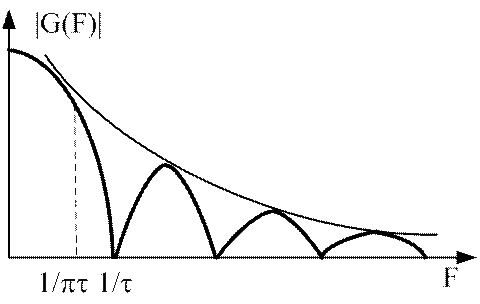
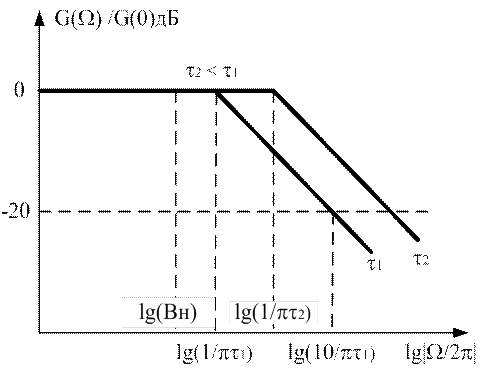
 При графическом изображении огибающей спектра по обеим
осям обычно используется логарифмический масштаб. В случае идеальных прямоугольных
импульсов огибающая спектра для двух значений длительности τ1 и
τ2 будет иметь вид, показанный на рисунке 2. Точка перелома
огибающих спектра (F = 1/πτ) соответствует точке, где огибающая спектра,
вычисляемая по выражению (3) касается первого лепестка спектра, определяемого
выражением (2) (а не точке, соответствующей первому нулю в спектре импульса).
При графическом изображении огибающей спектра по обеим
осям обычно используется логарифмический масштаб. В случае идеальных прямоугольных
импульсов огибающая спектра для двух значений длительности τ1 и
τ2 будет иметь вид, показанный на рисунке 2. Точка перелома
огибающих спектра (F = 1/πτ) соответствует точке, где огибающая спектра,
вычисляемая по выражению (3) касается первого лепестка спектра, определяемого
выражением (2) (а не точке, соответствующей первому нулю в спектре импульса).
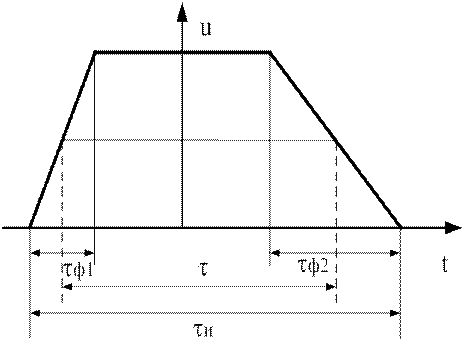
 Реальный импульс в отличие от прямоугольного имеет
конечную длительность переднего и заднего фронтов и аппроксимируется трапецией
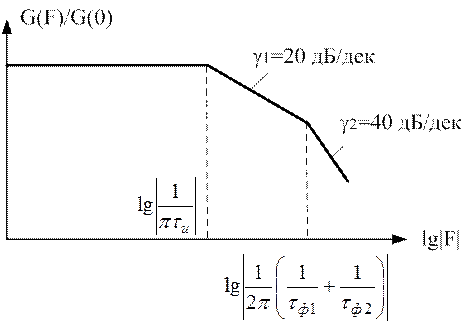
(рис. 3). Огибающая его спектра приведена на рисунке 4.
Реальный импульс в отличие от прямоугольного имеет
конечную длительность переднего и заднего фронтов и аппроксимируется трапецией
(рис. 3). Огибающая его спектра приведена на рисунке 4.
Начиная с частоты
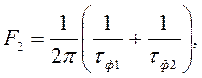
скорость спадания огибающей спектра увеличивается по сравнению со скоростью спадания огибающей спектра прямоугольного спектра до величины 40 дБ/декаду.
В общем случае скорость спадания огибающей спектра
зависит от непрерывности самого сигнала и его производных. Доказана теорема,
гласящая, что, если сигнал f(t) и его производные f/(t) … f(m-1)(t) непрерывны, а f(m)(t) конечна, то
при Ω→∞ огибающая спектра G(Ω) убывает не медленнее, чем ![]()
![]() , где
, где ![]() , или
γ(Ω) = 20 (m+1) дБ/декаду.
, или
γ(Ω) = 20 (m+1) дБ/декаду.
Эта теорема дает путь к построению сигналов, имеющих быстрое спадание внеполосных колебаний – чем более закруглен сигнал и все его производные, тем быстрее спадает огибающая спектра в зависимости
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.