Элементы проектирования цифровых фильтров.
Аппроксимация в процессе синтеза рекурсивных цифровых фильтров
Известно 3 группы методов расчета передаточных функций рекурсивного цифрового фильтра (РЦФ):
1. Метод преобразования аналоговых фильтров в цифровые. Это метод билинейного преобразования, метод инвариантности импульсной характеристики, метод согласованного Z-преобразования.
2. Прямой метод расчета РЦФ в Z-плоскости.
3. Методы, использующие алгоритмы оптимизации.
Метод билинейного преобразования
Для расчета частотно избирательных РЦФ (это ФНЧ, ФВЧ, ПФ, РФ) наиболее подходящим является метод билинейного Z-преобразования передаточной функции T(S) аналоговой в передаточную функцию H(S) цифрового фильтра. Широко известны следующие группы аналоговых фильтров:
1. Баттерворта с монотонно убывающей АЧХ, фильтр типа B
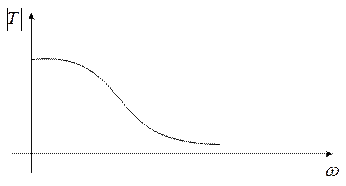
2. Чебышева с равноволновой в полосе пропускания и монотонно убывающей в полосе заграждения, фильтр типа T
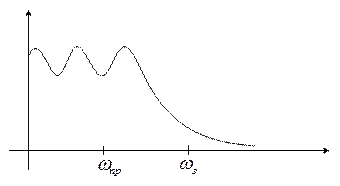
3. Инверсный Чебышева с монотонной в полосе пропускания и равноволновой в полосе заграждения, фильтр типа I
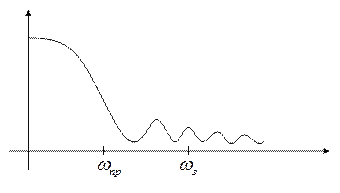
4. Золоторева-Кауера, фильтр типа C – эллиптический, АЧХ везде равноволновая.
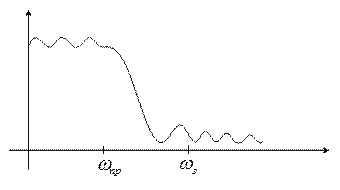
Эти фильтры подробно табулированы для любого из этих фильтров приводится передаточная функция T(S), вид АЧХ и связь граничных частот с параметрами фильтра. Это исходные данные для билинейного преобразования. Здесь используется конформное преобразование точек S-плоскости в точки Z-плоскости.
![]()
![]()
Между Z и S создается функциональная связь. Для каждого типа фильтров своя.
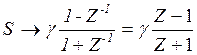
![]() - для
НЧ фильтра
- для
НЧ фильтра
![]() -
постоянный множитель, который не меняет форму преобразования, такая связь обеспечивает
однозначное преобразование передаточной функции аналогового фильтра прототипа T(S) в H(Z) РЦФ.
-
постоянный множитель, который не меняет форму преобразования, такая связь обеспечивает
однозначное преобразование передаточной функции аналогового фильтра прототипа T(S) в H(Z) РЦФ.
Каждой точке S плоскости ставиться в соответствие точка Z – плоскости. При этом мнимая ось ![]() преобразуется
на Z плоскости в
преобразуется
на Z плоскости в ![]()
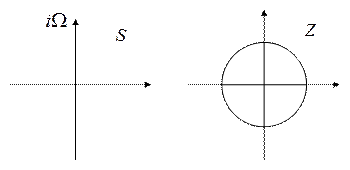
Все точки слева ![]() лежат внутри единичной окружности, это
значит, что аналоговый фильтр прототип устойчив, а значит устойчив и РЦФ.
лежат внутри единичной окружности, это
значит, что аналоговый фильтр прототип устойчив, а значит устойчив и РЦФ.
Соотношение между аналоговой и цифровой частотой нелинейно
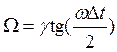
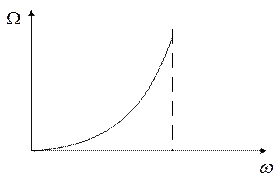
Для частотно избирательных
фильтров, у которых аппроксимация АЧХ имеет вид кусочнопостоянной функции,
такая зависимость между цифровой и аналоговой частотами не приводит к нарушению
избирательных свойств фильтра. Если параметр 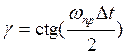 , то
перейдем к нормированному аналоговому фильтру прототипу
, то
перейдем к нормированному аналоговому фильтру прототипу ![]() .
Это для удобства использования справочников по фильтрам. Для каждого типа
фильтра есть свое билинейное преобразование.
.
Это для удобства использования справочников по фильтрам. Для каждого типа
фильтра есть свое билинейное преобразование.
|
Вид ЦФ |
Граничные частоты |
Замена |
Параметр |
Связь частот |
Граничные частоты |
|
НЧ |
|
|
|
|
|
|
ВЧ |
|
|
|
|
|
|
ПФ |
|
|
|
|
|
|
РФ |
|
|
|
|
|
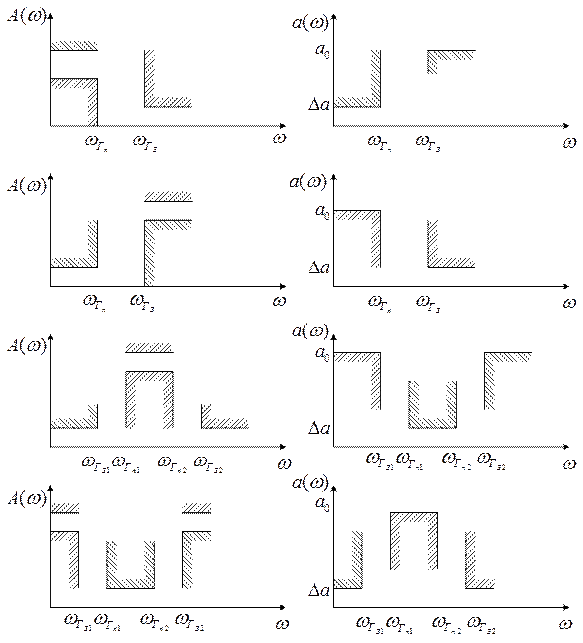
Порядок определения передаточной функции РЦФ.
Есть некоторые отличия для НЧ ВЧ
и ПФ РФ. Для НЧ ВЧ заданного типа исходными данными являются ![]() - частота дискретизации,
- частота дискретизации, ![]() и
и ![]() ,
верхняя граница рабочего затухания в полосе пропускания
,
верхняя граница рабочего затухания в полосе пропускания ![]() ,
граничное затухание в полосе заграждения
,
граничное затухание в полосе заграждения ![]() .
.
Определение передаточной функции идет по этапам:
1. Расчет
нормированных цифровых частот ![]() ,
, ![]()
2. Расчет
параметра преобразования ![]()
3. Нахождение
граничной аналоговой частоты ![]() полосы задержания
АФ-прототипа.
полосы задержания
АФ-прототипа.
4. Определение
передаточной функции АФ-прототипа (из справочника ![]() ,
, ![]() ,
, ![]() )
)
5. Определение передаточной функции H(Z) ЦФ с помощью билинейного Z-преобразования
6. Контрольный расчет АЧХ и затухания полученного фильтра
Для ПФ РФ отличие заключается в
том, что нужно больше исходных данных ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
Алгоритм определения H(Z) такой
же, но отличие в том, что на втором этапе определяются два параметра
.
Алгоритм определения H(Z) такой
же, но отличие в том, что на втором этапе определяются два параметра ![]() и
и ![]() .
.
Для билинейного преобразования в
полиномах 1-го порядка появится полином 2-го порядка, а в полиноме T(S) 2-го порядка появится полином ![]() 4-го порядка. При получении окончательного
выражения для H(Z) надо
разложить его на множители в виде 2-го порядка.
4-го порядка. При получении окончательного
выражения для H(Z) надо
разложить его на множители в виде 2-го порядка.
Практические методы реализации цифровых фильтров.
Различают 3 класса методов реализации ЦФ:
1. Метод свертки
2. Метод рекурсии
3. Метод преобразования Фурье
В зависимости от конкретных особенностей фильтра наиболее желательной может оказаться одна из трех реализаций, хотя это разбиение и условно.
Метод свертки основан на использовании импульсной характеристики фильтра:
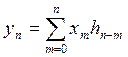 ,
применение этого метода возможно тогда, когда импульсная характеристика
является ограниченной во времени функцией. Это КИХ фильтр.
,
применение этого метода возможно тогда, когда импульсная характеристика
является ограниченной во времени функцией. Это КИХ фильтр.
Метод рекурсии основан на исходной форме разностного уравнения
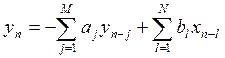 это
приводит к БИХ фильтру
это
приводит к БИХ фильтру
Метод преобразования Фурье основан на том, что дискретное преобразование свертки 2-х функций, это произведение ДПФ одной функции на комплексно сопряженное ДПФ другой функции
![]()
Каждый из методов имеет свои преимущества и свои недостатки. Применение первого метода позволяет получить линейную ФЧХ. Мощность собственных шумов НРЦФ << мощности шумов рекурсивного ЦФ. В НРЦФ эта мощность равна 0, если операции умножения и сложения выполняются точно, у РЦФ мощность шума не равна 0, т.к. в цепи обратной связи этого фильтра всегда выполняется округление при вычислении произведения отсчетов сигнала на коэффициенты фильтра. Исключением является ограниченный класс рекурсивных фильтров, имеющих ограниченные импульсные характеристики – однородные фильтры.
Для НРЦФ проще процесс вычисления его коэффициентов, т.к. аппроксимирующая функция линейно зависит от этих коэффициентов. В системах с изменением частоты дискретизации применение не рекурсивных ЦФ уменьшает число арифметических операций. Но у НРЦФ есть недостаток: при одинаковых требованиях к АЧХ, отсутствии требований к ФЧХ и постоянной частоте дискретизации они требуют выполнения значительно большего числа арифметических операций. В результате усложняется схемная реализация.
Третий метод используется, когда порядок фильтра большой. Его реализация по другим методам ведет к сложным схемам или длительным вычислениям. Здесь целесообразно реализовать фильтр на основе БПФ. Преимущество сказывается когда порядок фильтра > (28-30).
Примера цифровых фильтров
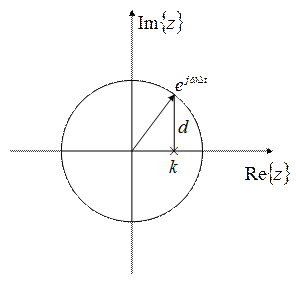
ЦФ первого порядка:
![]()
![]()
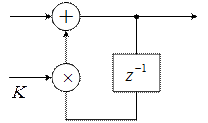
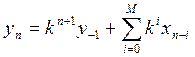
![]() , если
входной сигнал этого фильтра будет ступенчатая единичная функция
, если
входной сигнал этого фильтра будет ступенчатая единичная функция 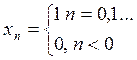
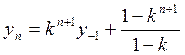
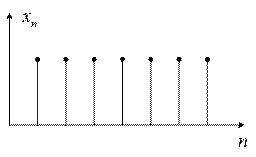
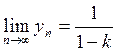
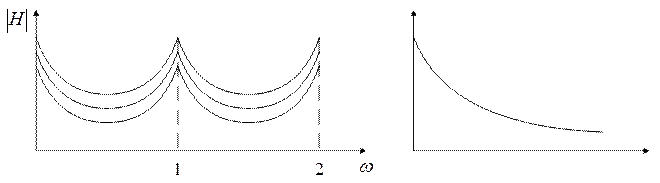
Переходные характеристики:
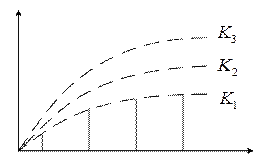
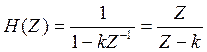
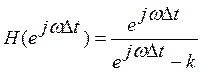
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.