Другие предметы \ Метрология, стандартизация и измерения в технике связи

Обработка результатов многократных измерений физической величины, проверка статистических гипотез и представление результата измерения

Страницы работы

29 страниц (Word-файл)

Скачать файл

Фрагмент текста работы

проверки принадлежности результатов наблюдений к нормальному распределению) рекомендуется распределение считать нормальным, так как надежность оценки повышается.

Расчетная часть

Техническое задание:

Физическая величина - мощность, размерность - Вт; средство измерения - ваттметр; разрешающая способность 0,02;

количество измерений ряда наблюдений n = 100;

уровень значимости q = 0,10;

доверительная вероятность Р_Д= 0,99.

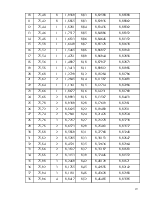
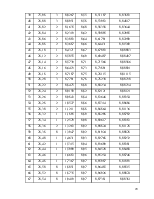
Результаты наблюдений приведены в таблице 1 (в Вт).

Таблица 1. Результаты наблюдений многократных прямых измерений.

i	1	2	3	4	5	6	7	8	9	10
x_i	75.90	76.20	76.36	75.74	75.96	76.00	75.92	76.16	75.20	76.44

i	11	12	13	14	15	16	17	18	19	20
x_i	75.98	75.68	76.18	75.54	76.40	76.74	75.70	75.96	75.94	76.24

i	21	22	23	24	25	26	27	28	29	30
x_i	75.48	76.22	75.62	76.18	75.88	75.26	75.44	76.24	76.02	76.42

i	31	32	33	34	35	36	37	38	39	40
x_i	75.94	76.12	75.78	75.92	76.48	75.50	76.66	76.14	76.10	75.76

i	41	42	43	44	45	46	47	48	49	50
x_i	75.84	75.80	75.60	76.26	76.06	75.96	75.86	75.58	76.30	76.20

i	51	52	53	54	55	56	57	58	59	60
x_i	75.98	75.82	75.84	75.72	75.90	76.36	76.12	75.82	75.80	75.64

i	61	62	63	64	65	66	67	68	69	70
x_i	76.34	76.04	76.22	75.78	75.56	75.76	76.00	76.04	76.28	76.26

i	71	72	73	74	75	76	77	78	79	80
x_i	76.02	76.08	75.74	75.52	76.46	75.88	76.62	75.94	75.72	76.08

i	81	82	83	84	85	86	87	88	89	90
x_i	76.30	75.96	75.70	75.68	75.46	76.00	75.90	76.14	76.20	75.98

i	91	92	93	94	95	96	97	98	99	100
x_i	76.28	76.16	75.62	75.30	75.92	75.66	76.32	75.86	75.76	76.06

Обработка ряда наблюдений.

Находим минимальный и максимальный член ряда наблюдений:

x_min= 75,20 Вт

x_max=76,74 Вт

Диапазон наблюдений разбиваем на r = 7 одинаковых интервалов Δx_j_,равных:

Δx_j= (x_max- x_min )/ r = 0,22 Вт

Δx_j = h = 0,22 Вт , j = 1...7

Таблица 2. Полученные интервалы.

1	75,20	75,42
2	75,42	75,64
3	75,64	75,86
4	75,86	76,08
5	76,08	76,30
6	76,30	76,52
7	76,52	76,74

Находим середины интервалов x_j и подсчитываем частоту каждого интервала:

Таблица 3. Расчетные данные.

j	x_j_, Вт	m_j		,1/Вт	η_j	η_j²	m_j_* η_j	m_j_* η_j²
1	75,31	3	0,03	0,14	-3	9	-9	27
2	75,53	11	0,11	0,50	-2	4	-22	44
3	75,75	21	0,21	0,95	-1	1	-21	21
4	75,97	29	0,29	1,32	0	0	0	0
5	76,19	22	0,22	1,0	1	1	22	22
6	76,41	11	0,11	0,50	2	4	22	44
7	76,63	3	0,03	0,14	3	9	9	27
Суммы:		100	-	-	-	-	1	185

Наибольшая частота приходится на пятый интервал, поэтому в качестве «ложного нуля» принимаем:

X₀ = X₄ =75,97 Вт.

Вычисляем статистические оценки вероятностей попадания результата наблюдений в j-ый интервал – частости по формуле:

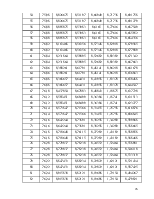
Вычисляем оценки средней плотности распределения в интервалах:

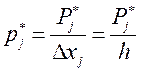Строим гистограмму статистического распределения (рис.1).

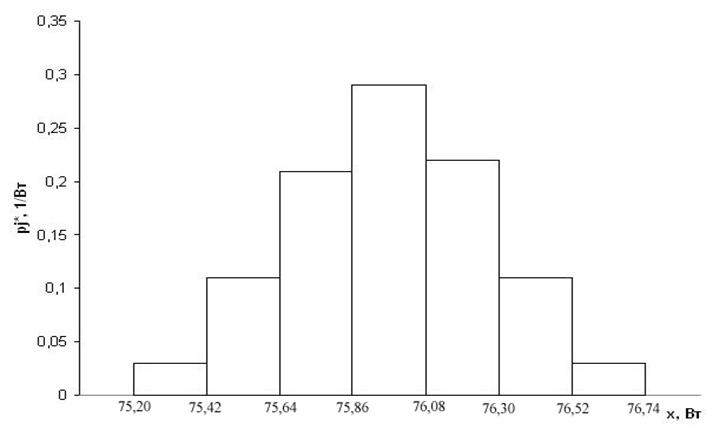
Рисунок 1. Гистограмма статистического распределения.

Из вида гистограммы можно сделать предположение, что закон распределения результатов наблюдений является нормальным.

Вычисляем для каждого интервала значение η_j:

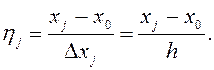
Находим значения начальных моментов:

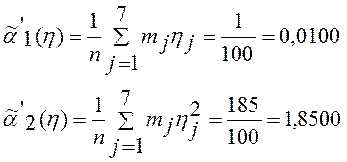
Вычисляем оценку второго центрального момента:

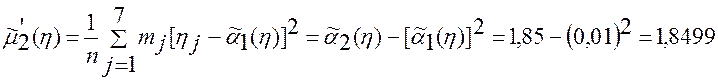
Определяем значения моментов наблюдений:

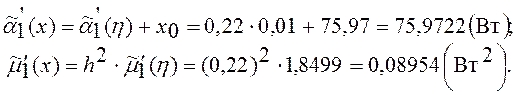
Вычисляем исправленные значения моментов:

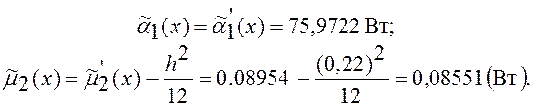
Определяем точные оценки истинного значения тока, с.к.о. результатов наблюдений и измерений:

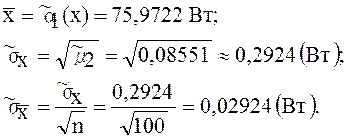
Проверяем наличие грубых погрешностей по критерию «трех сигм»:

=3^. =0,8772(Вт).

Наибольшие случайные отклонения равны:

|V(x_min)|=|x_min-|=|75,20–75,9722|=0,7722 < 0,8772 (Вт);

|V(x_max)| = | x_max-|=|76,74–75,9722|=0,7678 < 0,8772 (Вт).

Таким образом, среди результатов наблюдений нет таких, в которых были бы грубые погрешности.

Проверка нормальности закона распределения, используя критерии Колмогорова, χ², ω².

1. Критерий Колмогорова.

В таблицу 4 записываем значения: x_1;x₁+jΔ;…; x₁+kΔ, j=0,…,k, где Δ – разрешающая способность средства измерения ( измеряемое приращение интервала – Δ=0,02 Вт); k – число приращений интервала, вычисляемое по формуле:

k = (x_max –x_min)/D

k = (76,74-75,20)/ 0,02= 77;

Записываем частоты m_j₊₁(m₁,…,m_k₊₁), которые установлены для значений x₁,…,x₁+k^.Δ.

Вычисляем параметры опытного распределения:

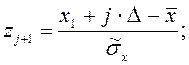
и определяем функции опытного распределения:

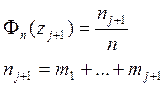
Определяем значения интегральной функции нормированного нормального распределения. Используем для этого значения нормированной функции Лапласа Ф^’(|z|) и формулу Ф(z)=0,5+ Ф^’(z), при этом Ф^’(z)= Ф^’(|z|) при z≥0 и Ф^’(z) = - Ф^’(|z|) при z<0.

По данным таблицы 6 находим максимальное абсолютное отклонение функции опытного распределения от функции теоретического распределения:

D_max= max|Ф_n(z_j₊₁)-Ф(z_j₊₁)|;

D_max= 0,04433;

Вычисляем значение проверяемого параметра:

l_n=D_max*= 0,04433*10= 0,4433.

Таблица 4. Рассчитанные значения.

j	x1+j*Δ	mj+1	zj+1	Фn(Zj+1)	Ф(Zj+1)	Фn(Zj+1)- Ф(Zj+1)
0	75,20	1	-2,6409	0,01	0,00415	0,00585
1	75,22	0	-2,5725	0,01	0,00508	0,00492
2	75,24	0	-2,5041	0,01	0,00621	0,00379
3	75,26	1	-2,4357	0,02	0,00734	0,01266
4	75,28	0	-2,3673	0,02	0,00889	0,01111
5	75,30	1	-2,2989	0,03	0,01072	0,01928
6	75,32	0	-2,2305	0,03	0,01287	0,01713
7	75,34	0	-2,1621	0,03	0,01559	0,01461
8	75,36	0	-2,0937	0,03	0,01831	0,01169
9	75,38	0	-2,0253	0,03	0,02118	0,00882
10	75,40	0	-1,9569	0,03	0,02500	0,00500
11	75,42	0	-1,8885	0,03	0,02938	0,00062
12	75,44	1	-1,8201	0,04	0,03438	0,00562
13	75,46	1	-1,7517	0,05	0,04006	0,00352
14	75,48	1	-1,6833	0,06	0,04648	0,01352
15	75,50	1	-1,6149	0,07	0,05370	0,01630
16	75,52	1	-1,5465	0,08	0,06057	0,01943
17	75,54	1	-1,4781	0,09	0,06944	0,02056
18	75,56	1	-1,4097	0,10	0,07927	0,02073
19	75,58	1	-1,3413	0,11	0,09012	0,01988
20	75,60	1	-1,2729	0,12	0,10204	0,01796
21	75,62	2	-1,2045	0,14	0,11507	0,02493
22	75,64	1	-1,1361	0,15	0,12714	0,02286
23	75,66	1	-1,0677	0,16	0,14231	0,01769
24	75,68	2	-0,9993	0,18	0,13567	0,04433
25	75,70	2	-0,9309	0,20	0,17619	0,02381
26	75,72	2	-0,8625	0,22	0,19489	0,02511
27	75,74	2	-0,7941	0,24	0,21476	0,02524
28	75,76	3	-0,7257	0,27	0,23270	0,03730
29	75,78	2	-0,6573	0,29	0,25463	0,03537
30	75,80	2	-0,5889	0,31	0,27760	0,03240
31	75,82	2	-0,5205	0,33	0,30153	0,02847
32	75,84	2	-0,4521	0,35	0,32636	0,02364
33	75,86	2	-0,3837	0,37	0,35197	0,01803
34	75,88	2	-0,3153	0,39	0,37448	0,01552
35	75,90	3	-0,2469	0,42	0,40129	0,01871
36	75,92	3	-0,1785	0,45	0,42858	0,02142
37	75,94	3	-0,1101	0,48	0,45620	0,02380
38	75,96	4	-0,0417	0,52	0,48405	0,03595
39	75,98	3	0,0267	0,55	0,51197	0,03803
40	76,00	3	0,0951	0,58	0,53983	0,04017
41	76,02	2	0,1635	0,60	0,56356	0,03644
42	76,04	2	0,2319	0,62	0,59095	0,02905
43	76,06	2	0,3003	0,64	0,61791	0,02209
44	76,08	2	0,3687	0,66	0,64431	0,01569
45	76,10	1	0,4371	0,67	0,67003	-0,00003
46	76,12	2	0,5055	0,69	0,69497	-0,00497
47	76,14	2	0,5739	0,71	0,71566	-0,00566
48	76,16	2	0,6423	0,73	0,73891	-0,00891
49	76,18	2	0,7107	0,75	0,76115	-0,01115
50	76,20	3	0,7791	0,78	0,78230	-0,00230
51	76,22	2	0,8475	0,80	0,80234	-0,00234
52	76,24	2	0,9159	0,82	0,82121	-0,00121
53	76,26	2	0,9843	0,84	0,83646	0,00354
54	76,28	2	1,0527	0,86	0,85314	0,00686
55	76,30	2	1,1211	0,88	0,86864	0,01136
56	76,32	1	1,1895	0,89	0,88298	0,00702
57	76,34	1	1,2579	0,90	0,89617	0,00383
58	76,36	2	1,3263	0,92	0,90824	0,01176
59	76,38	0	1,3947	0,92	0,91924	0,00076
60	76,40	1	1,4631	0,93	0,92768	0,00232
61	76,42	1	1,5315	0,94	0,93699	0,00301
62	76,44	1	1,5999	0,95	0,94520	0,00480
63	76,46	1	1,6683	0,96	0,95254	0,00746
64	76,48	1	1,7367	0,97	0,95907	0,01093
65	76,50	0	1,8051	0,97	0,96485	0,00515
66	76,52	0	1,8735	0,97	0,96926	0,00074
67	76,54	0	1,9419	0,97	0,97381	-0,00381
68	76,56	0	2,0103	0,97	0,97778	-0,00778
69	76,58	0	2,0787	0,97	0,98124	-0,01124
70	76,60	0	2,1471	0,97	0,98422	-0,01422
71	76,62	1	2,2155	0,98	0,98679	-0,00679
72	76,64	0	2,2839	0,98	0,98870	-0,00870
73	76,66	1	2,3523	0,99	0,99061	-0,00061
74	76,68	0	2,4207	0,99	0,99224	-0,00224
75	76,70	0	2,4891	0,99	0,99361	-0,00361
76	76,72	0	2,5575	0,99	0,99477	-0,00477
77	76,74	1	2,6259	1,00	0,99573	0,00427
		n=100				Dmax=0,04433

Так как q =0,10 , то = 1,36.

1-q = P{};

Так как = 0,4433< = 1,36 - то согласно критерию Колмогорова гипотеза о нормальности закона распределения подтверждается.

2. Критерий χ².

Для проверке нормальности закона распределения согласно критерию χ²данные расчетов привели в таблице.

Аналогично интервал от х_min=75,20 Вт до х_max=76,74 Вт разбили на r=7 интервалов. Значения середин интервалов x_j, частоты приведены в таблице.

Если в некоторых интервалах попало меньше пяти наблюдений, то такие интервалы объединили с соседними.

Нашли отклонения от середин каждого из интервалов V_j=_j-, а так же нормированные отклонения от среднего арифметического:

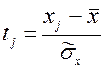Для каждого интервала исходя из значения t_j нашли дифференциальную функцию нормированного нормального распределения p(t_j). Плотность в серединах интервалов находятся из формул:

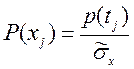Нашли теоретические частоты по формуле:

n^.P_j=n^.h_j^.P(x_j).

Нашли меру расхождения ;

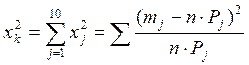
Таблица 5. Рассчитанные значения.

j	x_j, мА	mj	x_j-	t_j	P(t_j)	P(x_j)	nP_j=nΔx_j*P(x_j)	x²_j
1	75,31		-0,6622	-2,2647	0,0303	0,1036		0,3783
2	75,53		-0,4422	-1,5123	0,1276	0,4364		0,3783
3	75,75	18	-0,2222	-0,7599	0,2989	1,0222	22,4884	0,0985
4	75,97	19	-0,0022	-0,0075	0,3977	1,3601	29,9222	0,0284
5	76,19	27	0,2178	0,7449	0,3011	1,0298	22,6556	0,0190
6	76,41		0,4378	1,4973	0,1295	0,4429		0,2888
7	76,63		0,6578	2,2497	0,0317	0,1084		0,2888
		100

Число степеней свободы распределения k=r-s, где r=5, т.е. k=2.

Так как q/2=0,05

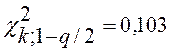
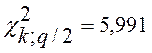
Учитывая, что:

< <

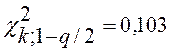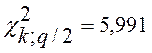
то распределение результатов можно считать нормальным.

3. Критерий ω².

Для проверки нормальности закона распределения согласно критерию ω² данные расчетов представили в таблице.

Результаты наблюдений располагаются в порядке возрастания, т.е. получается упорядоченная выборка ω²:

x₁≤x₂≤…≤x_n

Вычисляем значения нормированных отклонений от среднего арифметического:

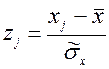Исходя из z_j находим значения интегральной функции нормированного нормального распределения Ф(z_j).

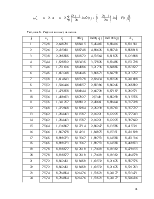
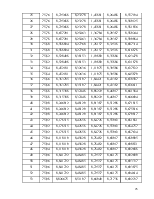
Вычисляем значения критерия проверки:

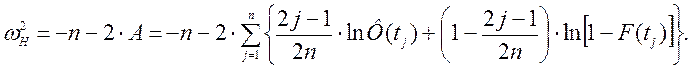
Таблица 6. Рассчитанные значения.

j	x_j	z_j	Ф(z_j)	ln(Ф(z_j))	ln(1-Ф(z_j))	A_j
1	75,20	-2,640791	0,00415	-5,48465	-0,00416	-0,031561
2	75,26	-2,435601	0,00740	-4,90628	-0,00743	-0,080910
3	75,30	-2,298808	0,01072	-4,53564	-0,01078	-0,123900
4	75,44	-1,820032	0,03438	-3,37028	-0,03498	-0,151720
5	75,46	-1,751636	0,04006	-3,21738	-0,04088	-0,183827
6	75,48	-1,683240	0,04648	-3,06873	-0,04759	-0,213757
7	75,50	-1,614843	0,05370	-2,92434	-0,05520	-0,241690
8	75,52	-1,546446	0,06057	-2,80396	-0,06248	-0,268092
9	75,54	-1,478050	0,06944	-2,66729	-0,07197	-0,292571
10	75,56	-1,409653	0,07927	-2,5349	-0,08259	-0,315558
11	75,58	-1,341257	0,09012	-2,40661	-0,09444	-0,337220
12	75,60	-1,272860	0,10204	-2,28239	-0,10763	-0,357727
13	75,62	-1,204463	0,11507	-2,16221	-0,12225	-0,377243
14	75,62	-1,204463	0,11507	-2,16221	-0,12225	-0,397642
15	75,64	-1,136067	0,12714	-2,06247	-0,13598	-0,415321
16	75,66	-1,067670	0,14231	-1,94975	-0,15351	-0,431929
17	75,68	-0,999273	0,13567	-1,99753	-0,14580	-0,451336
18	75,68	-0,999273	0,13567	-1,99753	-0,14580	-0,469853
19	75,70	-0,930877	0,17619	-1,73619	-0,19382	-0,479155
20	75,70	-0,930877	0,17619	-1,73619	-0,19382	-0,494579
21	75,72	-0,862481	0,19489	-1,63532	-0,21678	-0,507578
22	75,72	-0,862481	0,19489	-1,63532	-0,21678	-0,521763
23	75,74	-0,794084	0,21476	-1,53823	-0,24177	-0,533471
24	75,74	-0,794084	0,21476	-1,53823	-0,24177	-0,546436
25	75,76	-0,725688	0,23270	-1,45801	-0,26488	-0,557194
26	75,76	-0,725688	0,23270	-1,45801	-0,26488	-0,569125
27	75,76	-0,725688	0,23270	-1,45801	-0,26488	-0,581056
28	75,78	-0,657291	0,25463	-1,36794	-0,29387	-0,589244
29	75,78	-0,657291	0,25463	-1,36794	-0,29387	-0,599984
30	75,80	-0,588894	0,27760	-1,28157	-0,32518	-0,607314
31	75,80	-0,588894	0,27760	-1,28157	-0,32518	-0,616878
32	75,82	-0,520498	0,30153	-1,19889	-0,35886	-0,623470
33	75,82	-0,520498	0,30153	-1,19889	-0,35886	-0,631870
34	75,84	-0,452101	0,32636	-1,11975	-0,39506	-0,637832
35	75,84	-0,452101	0,32636	-1,11975	-0,39506	-0,645079
36	75,86	-0,383705	0,35197	-1,04421	-0,43382	-0,650507
37	75,86	-0,383705	0,35197	-1,04421	-0,43382	-0,656611
38	75,88	-0,315308	0,37448	-0,98222	-0,46917	-0,661564
39	75,88	-0,315308	0,37448	-0,98222	-0,46917	-0,666694
40	75,90	-0,246912	0,40129	-0,91307	-0,51298	-0,671015
41	75,90	-0,246912	0,40129	-0,91307	-0,51298	-0,675016
42	75,90	-0,246912	0,40129	-0,91307	-0,51298	-0,679017
43	75,92	-0,178515	0,42858	-0,84728	-0,55963	-0,681881
44	75,92	-0,178515	0,42858	-0,84728	-0,55963	-0,684757
45	75,92	-0,178515	0,42858	-0,84728	-0,55963	-0,687634
46	75,94	-0,110119	0,45620	-0,78482	-0,60917	-0,689095
47	75,94	-0,110119	0,45620	-0,78482	-0,60917	-0,690851
48	75,94	-0,110119	0,45620	-0,78482	-0,60917	-0,692608
49	75,96	-0,041722	0,48405	-0,72557	-0,66175	-0,692699
50	75,96	-0,041722	0,48405	-0,72557	-0,66175	-0,693337
51	75,96	-0,041722	0,48405	-0,72557	-0,66175	-0,693975
52	75,96	-0,041722	0,48405	-0,72557	-0,66175	-0,694614
53	75,98	0,026675	0,51197	-0,66949	-0,71738	-0,692237
54	75,98	0,026675	0,51197	-0,66949	-0,71738	-0,691758
55	75,98	0,026675	0,51197	-0,66949	-0,71738	-0,691279
56	76,00	0,095075	0,53983	-0,6165	-0,77616	-0,687549
57	76,00	0,095075	0,53983	-0,6165	-0,77616	-0,685952
58	76,00	0,095075	0,53983	-0,6165	-0,77616	-0,684356
59	76,02	0,163468	0,56356	-0,57348	-0,82910	-0,679565
60	76,02	0,163468	0,56356	-0,57348	-0,82910	-0,677009
61	76,04	0,231864	0,59095	-0,52602	-0,89392	-0,671342
62	76,04	0,231864	0,59095	-0,52602	-0,89392	-0,667663
63	76,06	0,300261	0,61791	-0,48141	-0,96210	-0,661670
64	76,06	0,300261	0,61791	-0,48141	-0,96210	-0,656863
65	76,08	0,368657	0,64431	-0,43958	-1,03370	-0,650488
66	76,08	0,368657	0,64431	-0,43958	-1,03370	-0,644547
67	76,10	0,437054	0,67003	-0,40043	-1,10875	-0,637720
68	76,12	0,505451	0,69499	-0,36386	-1,18741	-0,631513
69	76,12	0,505451	0,69499	-0,36386	-1,18741	-0,623277
70	76,14	0,573847	0,71566	-0,33455	-1,25758	-0,616076
71	76,14	0,573847	0,71566	-0,33455	-1,25758	-0,606845
72	76,16	0,642244	0,73891	-0,30258	-1,34289	-0,599068
73	76,16	0,642244	0,73891	-0,30258	-1,34289	-0,588665
74	76,18	0,710640	0,76115	-0,27292	-1,43192	-0,580058
75	76,18	0,710640	0,76115	-0,27292	-1,43192	-0,568468
76	76,20	0,779037	0,78230	-0,24552	-1,52464	-0,558901
77	76,20	0,779037	0,78230	-0,24552	-1,52464	-0,546110
78	76,20	0,779037	0,78230	-0,24552	-1,52464	-0,533319
79	76,22	0,847433	0,80234	-0,22022	-1,62121	-0,521434
80	76,22	0,847433	0,80234	-0,22022	-1,62121	-0,507425
81	76,24	0,915830	0,82121	-0,19698	-1,72154	-0,494267
82	76,24	0,915830	0,82121	-0,19698	-1,72154	-0,479021
83	76,26	0,984227	0,83646	-0,17858	-1,81070	-0,464198
84	76,26	0,984227	0,83646	-0,17858	-1,81070	-0,447877
85	76,28	1,052623	0,85314	-0,15883	-1,91828	-0,431545
86	76,28	1,052623	0,85314	-0,15883	-1,91828	-0,413951
87	76,30	1,121020	0,86864	-0,14083	-2,02981	-0,395840
88	76,30	1,121020	0,86864	-0,14083	-2,02981	-0,376950
89	76,32	1,189416	0,88298	-0,12445	-2,14541	-0,356863
90	76,34	1,257813	0,89617	-0,10963	-2,26500	-0,335940
91	76,36	1,326210	0,90824	-0,09625	-2,38858	-0,314018
92	76,36	1,326210	0,90824	-0,09625	-2,38858	-0,291095
93	76,40	1,463002	0,92768	-0,07507	-2,62665	-0,266437
94	76,42	1,531399	0,93699	-0,06508	-2,76446	-0,240542
95	76,44	1,599796	0,94520	-0,05636	-2,90407	-0,212983
96	76,46	1,668192	0,95254	-0,04862	-3,04787	-0,183589
97	76,48	1,736589	0,95907	-0,04179	-3,19589	-0,152185
98	76,62	2,215364	0,98679	-0,0133	-4,32678	-0,121135
99	76,66	2,352158	0,99061	-0,00943	-4,66811	-0,079314
100	76,74	2,625744	0,99573	-0,00428	-5,45614	-0,031538