Изучение номенклатуры бытовой радиоэлектронной аппаратуры и освоение методики определения параметров системы массового обслуживания (сервисного центра), страница 2

По конструктивно-технологическим признакам

1	Конструктивная группа	2	Группа сложности
	I - стационарная		0, 1, 2, 3, 4 - для отечественной БРА
	II - переносная		Hi -Fi., массового производства - для зарубежной БРА
	III - носимая
	IV - автомобильная
3	Конструктивное исполнение и назначение
	Однокорпусная (моноблочная)
	Разъемная (блочная или компонент)

[ По желанию пользователя те или иные компоненты можно объединять звуковые или видеозвуковые системы , формируя полный цикл приема, обработки и воспроизведения информации].

К моноблочным видам БРА можно отнести:

- радиоприемные устройства (переносные, носимые, стационарные, автомобильные), в том числе магнитолы, магниторадиолы;

- телевизионные приемники;

- магнитофоны, плейеры;

- электрофоны;

- камкодеры.

К разъемным (блочным) видам аппаратуры:

- усилители;

- тюнеры;

- магнитофонные деки;

- акустические системы

- электропроигрыватели;

- уст-ва телеигр;

- наушники, микрофоны.

II. Общие положения теории массового обслуживания.

СИСТЕМОЙ МАССОВОГО ОБСЛУЖИВАНИЯ (СМО) называется система, состоящая из n обслуживающих единиц, называемых каналами обслуживания.

В результате своего функционирования СМО удовлетворяет поток заявок, представляющий собой поток случайных величин (СВ). Практический интерес представляет простейший поток заявок, отвечающий следующим свойствам:

- ординарности (невозможностью одномоментного появления двух заявок);

- стационарности (появление некоторого числа заявок на интервале времени Dt не зависит от t, т.е. от расположения Dt на оси времени);

- отсутствия последействия (для двух интервалов времени Dt₁ и Dt₂ число заявок в одном из них не зависит от числа заявок , попадающих в другой).

Для простейшего потока вероятность того, что в интервале времени t к обслуживанию будет принято k заявок ( на интервал t попадает k заявок)

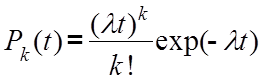, (1)

где l - интенсивность протока заявок.

Если число заявок на обслуживание превышает число каналов k > n, то заявки устанавливаются в очередь на обслуживание (СМО с ожиданием).

III. Расчет параметров конкретной СМО с использованием математического аппарата теории массового обслуживания.

Постановка задачи - расчет характеристик сервисного центра БРА, работу которого можно описать как функционирование СМО с n каналами (мастерами), на вход которой поступает k заявок с вероятностью , описываемой формулой (1), в которой l - среднее число заявок.

Известно из статистических данных, что случайная величина - среднее время обслуживания (среднее время ремонта аппарата) Т_СР, имеет экспоненциальный закон распределения

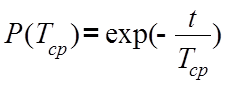, (2)

где n = 1/ Т_СР - параметр распределения.

Предполагается, что число заявок на обслуживание может превышать число каналов, т.е. имеется в виду СМО с ожиданием.

Требуется:

1. Определить число каналов обслуживания, исходя из условия ограниченной очереди.

2. Определить длину очереди М₁.

3. Оценить эффективность работы сервисного центра по следующим параметрам:

3.1. Загруженность мастеров (незанятое время работника).

3.2. Оценка параметров очереди:

- среднее время ожидания начала ремонта (Т_ОЖ);

- вероятность начала ремонта, определяющая долю заявок реализуемую не позже времени Т_ОЖ.

Решение.

1.Определение необходимого числа каналов.

Производится из условия выполнения требования об ограниченности очереди. Известно, что при соотношении ( l/n ) ³ n очередь неограниченно возрастает. Следовательно необходимо, чтобы

n > l/n (3)

2. Определение длины очереди при условии, что все каналы заняты.

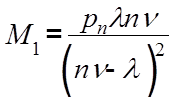, (4)

где p_n - вероятность того, что все каналы заняты, т.е число заявок в точности равно числу каналов

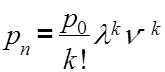, (5)

где p₀ - вероятность того, что в момент поступления заявки все каналы свободны

p₀= 1/[S(1/k!)(l/n)^k + lⁿ /(n-1)!(nn - l)(n)^n-1] (6)

k=0

3.1. Среднее число свободных каналов

n-1

1 2 3

Скачать файл