Отделение корней уравнения. Метод итераций. Блок-схема алгоритма решения задачи, страница 3

Рис.5 Входные параметры (a,b,e)

 

Из двух отрезков [a; x₀] и [x₀, b] выберем тот, на концах которого функция f(x) имеет противоположные знаки (т.е. отрезок, содержащий корень уравнения). Проведя секущую на новом отрезке [a; b], получим второе приближение корня x₂. Процесс вычисления приближений по формуле (3) продолжаем до выполнения неравенства x_n+1 - x_n  <= E.  

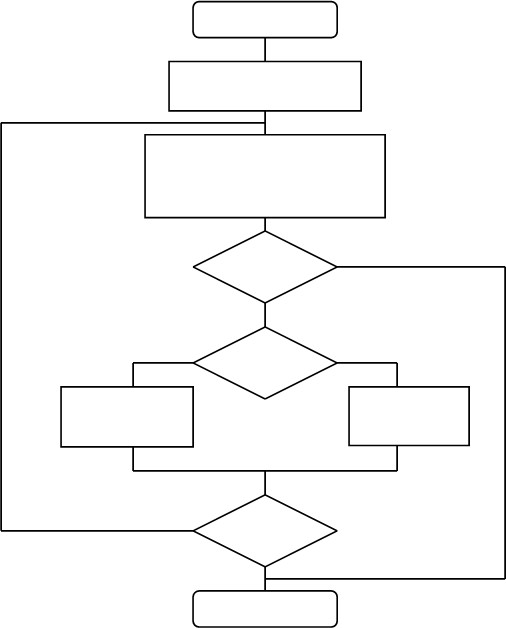
Схема алгоритма уточнения корня уравнения методом хорд приведена на рис. 5.

В схеме алгоритма:

2 - вычисление значений функции f(a) и f(b);

присвоение начального значения a текущему приближению корня x;

3 - запоминание предыдущего приближения корня x в переменной u;

вычисление очередного приближения корня x по формуле (2);

4 - проверка условия f(x) = 0. Если условие выполняется, то x - корень уравнения, - выход из алгоритма;

5-7 - определение нового отрезка [a; b], содержащего корень, значение y присваивается переменным z или t в зависимости от того, какая граница a или b сдвигается в точку x;

8 - проверка условия окончания вычисления корня.

Блок-схема алгоритма решения задачи

Программа решения задачи

PROGRAM KURS;

VAR

A:ARRAY [1..3] OF REAL;

B:ARRAY [1..2] OF REAL;

X,H,E,XK:REAL;

N,I,J:BYTE;

{Заданная функция}

FUNCTION F(A1,B1,X:REAL):REAL;

BEGIN

F:=X-B1/(A1+SIN(X))

END;

{Процедура уточнения корней}

PROCEDURE KOR(A,B,MIN,MAX,E:REAL;VAR N:BYTE;VAR K:REAL);

VAR

X,Y,X1,X2,Y1,Y2:REAL;

BEGIN

X1:=MIN;

X2:=MAX;

Y1:=F(A,B,MIN);

Y2:=F(A,B,MAX);

N:=0;

REPEAT

X:=(X1+X2)/2;

Y:=F(A,B,X);

IF Y1*Y<0

THEN BEGIN

Y2:=Y;

X2:=X

END

ELSE BEGIN

Y1:=Y;

X1:=X

END;

N:=N+1;

UNTIL (ABS(X1-X2)<E)OR(N=100);

IF N<>100

THEN K:=X

END;

{Основная программа}

BEGIN

FOR I:=1 TO 3 DO

BEGIN

WRITE('Введите A',I,'=');

READLN(A[I])

END;

WRITE('Введите B1=');

READLN(B[1]);

WRITE('Введите B2=');

READLN(B[2]);

WRITE('Введите погpешность ');

READLN(E);

WRITE('Введите шаг ');

READLN(H);

{Отделение корней}

FOR I:=1 TO 3 DO

FOR J:=1 TO 2 DO

BEGIN

X:=0;

REPEAT

IF F(A[I],B[J],X)*F(A[I],B[J],X+H)<0

THEN BEGIN

KOR(A[I],B[J],X,X+H,E,N,XK);

IF N=100

THEN WRITELN(' ')

ELSE WRITELN('Корень: ',XK:6:4,'   Число итераций = ',N,' при А=',a[i]:3:1,' и B=',b[j]:3:2 )

END;

X:=X+H

UNTIL X>6.5

END;

END.

Результаты вычисления по программе

Введите A1=1.6

Введите A2=1.7

Введите A3=1.8

Введите B1=5.0

Введите B2=5.1

Введите погpешность 1E-3

Введите шаг 0.1

Корень: 1.9883   Число итераций = 7 при А=1.6 и B=5.00

Корень: 3.1586   Число итераций = 7 при А=1.6 и B=5.00

Корень: 5.5164   Число итераций = 7 при А=1.6 и B=5.00

Корень: 2.0508   Число итераций = 7 при А=1.6 и B=5.10

Корень: 3.0930   Число итераций = 7 при А=1.6 и B=5.10

Корень: 5.5367   Число итераций = 7 при А=1.6 и B=5.10

Корень: 1.8867   Число итераций = 7 при А=1.7 и B=5.00

Корень: 3.3508   Число итераций = 7 при А=1.7 и B=5.00

Корень: 5.3977   Число итераций = 7 при А=1.7 и B=5.00

Корень: 1.9367   Число итераций = 7 при А=1.7 и B=5.10

Корень: 3.2945   Число итераций = 7 при А=1.7 и B=5.10

Корень: 5.4211   Число итераций = 7 при А=1.7 и B=5.10

Корень: 1.8023   Число итераций = 7 при А=1.8 и B=5.00

Корень: 3.5398   Число итераций = 7 при А=1.8 и B=5.00

Корень: 5.2664   Число итераций = 7 при А=1.8 и B=5.00

Корень: 1.8461   Число итераций = 7 при А=1.8 и B=5.10

Корень: 3.4852   Число итераций = 7 при А=1.8 и B=5.10

Корень: 5.2930   Число итераций = 7 при А=1.8 и B=5.10

Краткие выводы по решению задачи

В данной курсовой работе очень широко используются подпрограммы (подпрограммы и функции), это позволяет сократить размер программы и сделать её более понятной для пользователя. Такой способ значительно упрощает вычисление промежуточных значений. Программа построенная по данному алгоритму наиболее оптимально использует возможности ПЭВМ. Рабочий интерфейс разработан в соответсвии с заданием на курсовую работу, что облегчает просмотр результатов выполнения программы. Вся практическая работа была выполнена в соответствии с рекомендациями изложенными в теоретической части курсовой работы.

Графическое решение решение задачи доказывает то, что программа работает правильно

Графическое решение задачи

Список используемой литературы

1.  Новичков В. С., Парфилова Н. И. “Алгоритмические языки в техникуме. Паскаль”, Москва, Высшая школа, 1994 год.

2.  Киселёв А. В. Коротаев А. Т. “Практическая работа на персональном компьютере”, Москва, 1995 год.

3.  Фигурнов В. Э.” IBM PC для пользователя ”, Москва, Финансы и статистика, 1991 год.

4.  Фаронов В. В. “ Програмирование на персоональных ЭВМ в среде Турбо-Паскаль “, Москва,  Изд-во МГТУ, 1991 год.