Отделение корней уравнения. Метод итераций. Блок-схема алгоритма решения задачи

Содержание

Задание к курсовой работе ..................... 2

Теоретическая часть :

  1. Отделение корней уравнения ................ 3

  2. Метод итераций............................ 5

  3. Метод Ньютона............................. 7

  4. Метод половинного деления ................. 9

  5. Метод хорд............................... 11

Блок-схема алгоритма решения задачи  ......... 13

Программа решения задачи ..................... 16

Результаты вычисления по программе ........... 18

Краткие выводы по решению задачи ............. 19

Список используемой литературы ............... 21

Задание к курсовой работе

Составить программу отделения и вычисления с погрешностью

e всех действительных корней уравнения f(x) = 0 заданным методом. Метод решения и исходные данные выбрать из таблиц 1 и 2 в соответствии с номером варианта.

В программе предусмотреть защиту от зацикливания итерационного процесса, подсчет и вывод на печать числа итераций, за которое удается найти значение корня с заданной погрешностью. Для контроля правильности результата включить в программу вычисление и печать значения функции при найденном значении корня.

Таблица № 1

Метод половинного деления

Таблица № 2

x - b / (a + sin x), где а = 1,6; 1,7; 1,8; b = 5; 5,1; e=10^-3

1. Отделение корней уравнения

Решение уравнения приближенными методами состоит из двух этапов:

- отделение корней, т.е. отыскание достаточно малых областей, в каждой из которых заключен один и только один корень уравнения;

- вычисление корней с заданной погрешностью.

Для отделения корней следует воспользоваться правилом: если значения непрерывной функции f(x) на концах некоторого отрезка имеют разные знаки, то внутри отрезка содержится по меньшей мере один корень уравнения f(x) = 0.

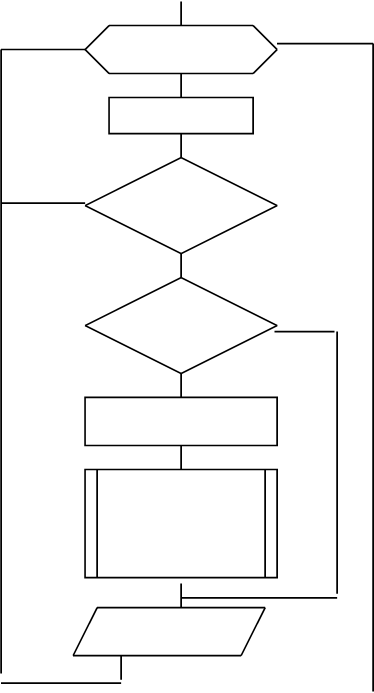
Рис.1 входные параметры (X0,XK,H,E)

 

Отделить корни можно графическим способом, построив график функции f(x) и выделив все участки, на которых содержится только один корень.

Однако, если уравнение имеет несколько корней, целесообразнее этот этап проводить с помощью ЭВМ. Отделение корней при этом заключается в вычислении значений функции f(x) на интервале [x₀ ; x_k ], содержащем все корни, с некоторым шагом h (рис. 1). Вычисление значений функции происходит до первой смены ее знака, за интервал изоляции корня [a;b]  принимается последний участок длиной h, на концах которого функция имеет разные знаки. Далее осуществляется уточнение корня заданным методом, и процесс вычисления значений функции до смены ее знака повторяется. Чтобы приведенный на рис. 1 алгоритм вычислял все корни заданного уравнения, необходимо предварительно провести графическое исследование функции f(x) с целью определения интервала [x₀; x_k ], содержащего все корни, и значения шага h, величина которого должна быть меньше минимального расстояния между корнями уравнения.

Возможна ситуация, когда значение функции y в очередной точке x равно нулю (блок 6). Это означает, что x - корень уравнения, этап уточнения корня (блоки 7,8) при этом не выполняется, результаты выводятся на печать, и процесс поиска корней продолжается.

При изложении методов уточнения корней уравнения будем считать, что нам известен отрезок [a; b], внутри которого существует только один корень уравнения (назовем его x^* ).

2. Метод итераций

Исходное уравнение f(x) = 0 преобразуем к виду x = f (x), что всегда можно сделать и притом многими способами. Выберем на отрезке [a; b] произвольную точку x₀ - нулевое приближение корня и примем в качестве следующего приближения x₁= f (x₀), далее x₂ = f (x₁) и т.д. В общем случае x_n = f (x_n-1). Этот процесс последовательного вычисления чисел x_n (n = 1, 2, 3...) называется методом итераций.

Если на отрезке [a; b] , содержащем корень уравнения, выполняется условие f ^/(x) <= q < 1, то процесс итераций сходится, т.е. увеличивая n, можно получить приближение, сколь угодно мало отличающееся от значения корня x^* . Процесс итераций следует продолжать до тех пор, пока не будет обеспечено выполнение неравенства

 

x_n - x_n-1  <= [(1 - q) / q] E .

При практическом нахождении корней по методу итераций нужно стремиться, чтобы производная y^/(x) по абсолютной величине была как можно меньше 1. В этом случае корень будет всегда найден, и чем меньше величина q, тем меньше число итераций для этого потребуется.

Рис. 2  входные парамтры (a,b,e,q)