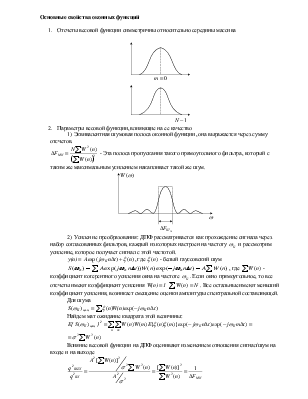

Основные свойства оконных функций
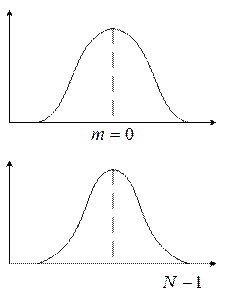
1) Эквивалентная шумовая полоса оконной функции, она выражается через сумму отсчетов.
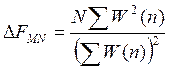 - Эта
полоса пропускания такого прямоугольного фильтра, который с таким же
максимальным усилением накапливает такой же шум.
- Эта
полоса пропускания такого прямоугольного фильтра, который с таким же
максимальным усилением накапливает такой же шум.
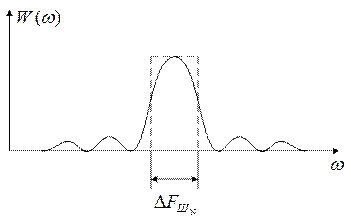
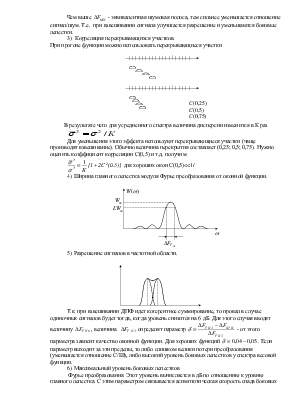
2) Усиление преобразования: ДПФ
рассматривается как прохождение сигнала через набор согласованных фильтров,
каждый из которых настроен на частоту ![]() и
рассмотрим усиление, которое получает сигнал с этой частотой.
и
рассмотрим усиление, которое получает сигнал с этой частотой.
![]() , где
, где ![]() - белый
гауссовский шум
- белый
гауссовский шум
![]() , где
, где ![]() - коэффициент
когерентного усиления окна на частоте
- коэффициент
когерентного усиления окна на частоте ![]() . Если
окно прямоугольное, то все отсчеты имеют коэффициент усиления
. Если
окно прямоугольное, то все отсчеты имеют коэффициент усиления ![]()
![]() . Все остальные имеют
меньший коэффициент усиления, возникает смещение оценки амплитуды спектральной
составляющей.
. Все остальные имеют
меньший коэффициент усиления, возникает смещение оценки амплитуды спектральной
составляющей.
Для шума
![]()
Найдем мат ожидание квадрата этой величины:
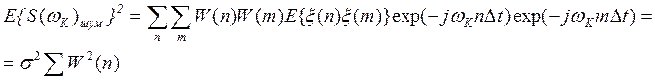
Влияние весовой функции на ДПФ оценивают изменением отношения сигнал/шум на входе и на выходе
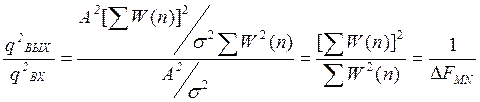
Чем выше ![]() - эквивалентная шумовая полоса, тем
сильнее уменьшается отношение сигнал/шум. Т.е. при взвешивании сигнала
улучшается разрешение и уменьшаются боковые лепестки.
- эквивалентная шумовая полоса, тем
сильнее уменьшается отношение сигнал/шум. Т.е. при взвешивании сигнала
улучшается разрешение и уменьшаются боковые лепестки.
3) Корреляция перекрывающихся участков. При прогоне функции можно использовать перекрывающиеся участки
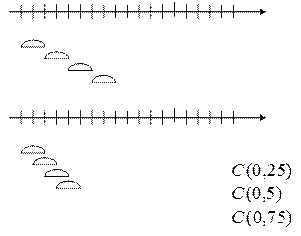
В результате чего для усредненного спектра величина дисперсии изменится в К раз
![]()
Для уменьшения этого эффекта используют перекрывающиеся участки (чаще производят взвешивание). Обычно величина перекрытия составляет (0,25; 0,5; 0,75). Нужно оценить коэффициент корреляции С(0,5) и т.д. получим
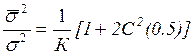 для хороших окон С(0,5)<<1/
для хороших окон С(0,5)<<1/
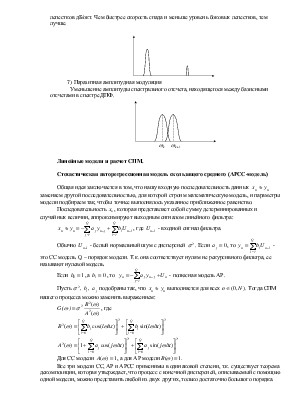
4) Ширина главного лепестка модуля Фурье преобразования от оконной функции.
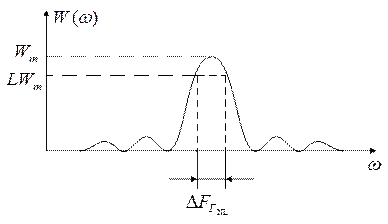
5) Разрешение сигналов в частотной области.
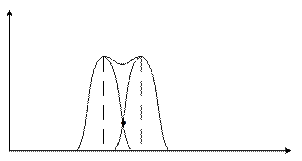
Т.к. при
взвешивании ДПФ идет когерентное суммирование, то провал в случае одиночных
сигналов будет тогда, когда уровень снизится на 6 дБ. Для этого случая вводят
величину ![]() , величина
, величина ![]() определят
параметр
определят
параметр 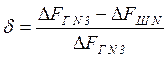 - от этого параметра зависит качество
оконной функции. Для хороших функций
- от этого параметра зависит качество
оконной функции. Для хороших функций ![]() . Если параметр выходит
за эти пределы, то либо слишком велики потери преобразования (уменьшается отношение
С/Ш), либо высокий уровень боковых лепестков у спектра весовой функции.
. Если параметр выходит
за эти пределы, то либо слишком велики потери преобразования (уменьшается отношение
С/Ш), либо высокий уровень боковых лепестков у спектра весовой функции.
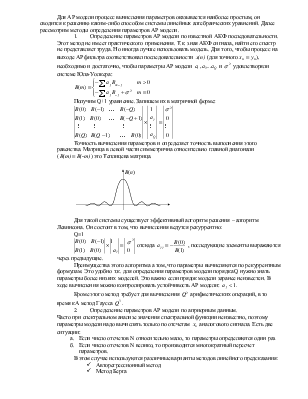
6) Максимальный уровень боковых лепестков
Фурье преобразования. Этот уровень вычисляется в дБ по отношению к уровню главного лепестка. С этим параметром связывается асимптотическая скорость спада боковых лепестков дБ/окт. Чем быстрее скорость спада и меньше уровень боковых лепестков, тем лучше.
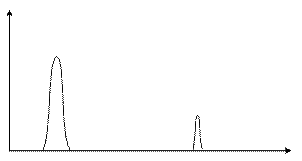
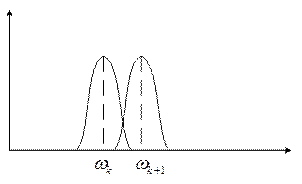
7) Паразитная амплитудная модуляция
Уменьшение амплитуды спектрального отсчета, находящегося между базисными отсчетами в спектре ДПФ.
Линейные модели и расчет СПМ.
Стохастическая авторегрессионная модель скользящего среднего (АРСС-модель)
Общая идея заключается в том,
что нашу входную последовательность данных ![]() заменяем
другой последовательностью, для которой строим математическую модель, и
параметры модели подбираем так, чтобы точнее выполнялось указанное приближенное
равенство.
заменяем
другой последовательностью, для которой строим математическую модель, и
параметры модели подбираем так, чтобы точнее выполнялось указанное приближенное
равенство.
Последовательность ![]() , которая представляет собой сумму
детерминированных и случайных величин, аппроксимируют выходным сигналом
линейного фильтра:
, которая представляет собой сумму
детерминированных и случайных величин, аппроксимируют выходным сигналом
линейного фильтра:
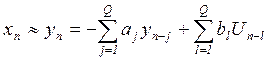 , где
, где ![]() - входной сигнал фильтра.
- входной сигнал фильтра.
Обычно ![]() -
белый нормальный шум с дисперсией
-
белый нормальный шум с дисперсией ![]() . Если
. Если ![]() , то
, то 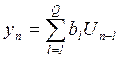 - это
СС модель. Q – порядок модели. Т.к. она соответствует
нулям не рекурсивного фильтра, ее называют нулевой модель.
- это
СС модель. Q – порядок модели. Т.к. она соответствует
нулям не рекурсивного фильтра, ее называют нулевой модель.
Если ![]() , а
, а ![]() , то
, то 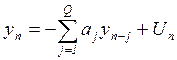 -
полюсная модель АР.
-
полюсная модель АР.
Пусть ![]() ,
,
![]() ,
, ![]() подобраны
так, что
подобраны
так, что ![]() выполняется для всех
выполняется для всех ![]() . Тогда СПМ нашего процесса можно заменить
выражением:
. Тогда СПМ нашего процесса можно заменить
выражением:
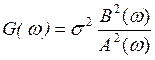 , где
, где
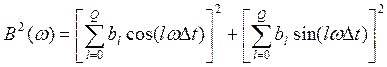
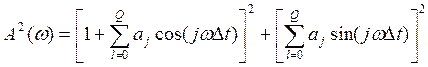
Для СС модели ![]() , а для АР модели
, а для АР модели![]() .
.
Все три модели СС, АР и АРСС применимы в одинаковой степени, т.к. существует теорема декомпозиции, которая утверждает, что процесс с конечной дисперсией, описываемый с помощью одной модели, можно представить любой из двух других, только достаточно большого порядка.
Для АР модели процесс вычисления параметров оказывается наиболее простым, он сводится к решению каким-либо способом системы линейных алгебраических уравнений. Далее рассмотрим методы определения параметров АР модели.
1.
Определение параметров АР модели по известной АКФ последовательности.
Этот метод не имеет практического применения. Т.к. зная АКФ сигнала, найти его
спектр не представляет труда. Но иногда лучше использовать модель. Для того,
чтобы процесс на выходе АР фильтра соответствовал последовательности ![]() (для точного
(для точного![]() ), необходимо
и достаточно, чтобы параметры АР модели
), необходимо
и достаточно, чтобы параметры АР модели ![]() и
и ![]() удовлетворяли системе Юла-Уолкера:
удовлетворяли системе Юла-Уолкера:
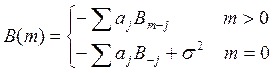
Получим Q+1 уравнение. Запишем их в матричной форме:
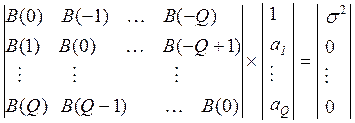
Точность
вычисления параметров и определяет точность выполнения этого равенства. Матрица
в левой части симметрична относительно главной диагонали (![]() ) это Теплицева матрица.
) это Теплицева матрица.
Для такой системы существует эффективный алгоритм решения – алгоритм Левинсона. Он состоит в том, что вычисления ведутся рекуррентно:
Q=1
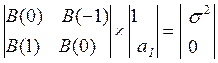 отсюда
отсюда 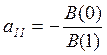 ,
последующие элементы выражаются через предыдущие.
,
последующие элементы выражаются через предыдущие.
Преимущества
этого алгоритма а том, что параметры вычисляются по рекуррентным формулам. Это
удобно т.к. для определения параметров модели порядка Q нужно знать параметры более низких моделей. Это важно если
прядок модели заранее неизвестен. В ходе вычисления можно контролировать
устойчивость АР модели: ![]() .
.
Кроме этого
метод требует для вычисления ![]() арифметических
операций, в то время кА метод Гаусса
арифметических
операций, в то время кА метод Гаусса ![]() .
.
2. Определение параметров АР модели по априорным данным.
Часто при спектральном анализе значения
спектральной функции неизвестно, поэтому параметры модели надо вычислять только
по отсчетам ![]() аналогового сигнала. Есть две ситуации:
аналогового сигнала. Есть две ситуации:
а. Если число отсчетов N относительно мало, то параметры определяются один раз б. Если число отсчетов N велико, то производится многократный пересчет параметров.
В этом случае используются различные варианты методов линейного предсказания:
ü Авторегрессионный метод
ü Метод Берга
В любом случае для метода линейного предсказания имеем N отсчетов, предшествующих Q при предсказании вперед.
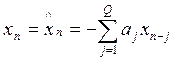 Ошибка
Ошибка 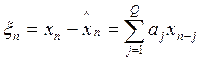
![]()
Это
выражение дает нам мгновенную ошибку предсказания вперед обозначим ее ![]() . Здесь надо минимизировать общую ошибку:
. Здесь надо минимизировать общую ошибку:
![]() - используем для определения
коэффициентов. Различные варианты метода линейного предсказания отличаются
выбором данных значений n, если использовать
автокорреляционный метод, то
- используем для определения
коэффициентов. Различные варианты метода линейного предсказания отличаются
выбором данных значений n, если использовать
автокорреляционный метод, то ![]() при этом
при этом
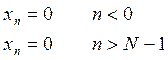
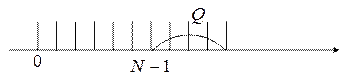
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.