Абсолютная угловая скорость. Вектор переносной скорости, мгновенная ось

рад/с.

Подставляя в (а), получим:

м/с.

Вектор переносной скорости  изобразим перпендикулярно радиусу переносного вращения  в сторону  (рис. 2.108).

Для определения направления абсолютной скорости  сложим векторы составляющих скоростей по правилу параллелограмма, а модуль  определим по формуле

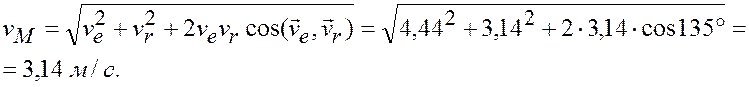
3. Определение абсолютного ускорения . Так как переносное движение  поступательное, то воспользуемся теоремой Кориолиса

.

Относительное ускорение  можно определить по зависимости

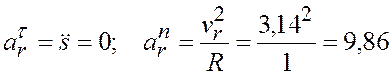, где                              м/с².

На рис. 2.109 изобразим , направив вектор от точки М к центру окружности.

Переносное ускорение  определится по формуле

, где

м/с².

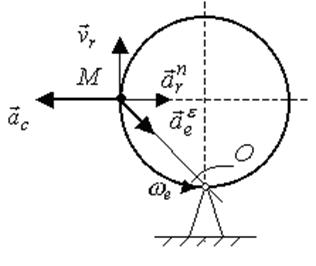
Рис. 2.109

Вектор  имеет начало в точке М и направлен вдоль радиуса переносного вращения ОМ к центру О.

Ускорение Кориолиса равно

.

Вектор угловой скорости  направлен вдоль оси вращения,т.е. вдоль прямой, перпендикулярной плоскости чертежа, а вектор относительной скорости   лежит в плоскости чертежа, т.е. в любой момент времени угол между  и  равен , а 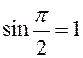. Поэтому

 м/с².

Для показа   воспользуемся правилом Жуковского. Так как  уже находится в плоскости, перпендикулярной оси переносного вращения, повернем его на 90^о в сторону , т.е. против хода часовой стрелки.

Модуль абсолютного ускорения определим по методу проекций:

;

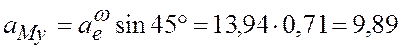 м/с², отсюда

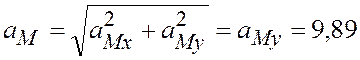м/с².

7.5. Сложение  вращений твердого тела вокруг двух

параллельных осей

Пусть твердое тело вращается вокруг оси Оz (рис. 2.110) с относительной угловой скоростью  (относительное движение  по отношению к осям Oxyz), а система осей Oxyz вращается вокруг оси O₁z₁ параллельной оси Оzс переносной угловой скоростью  (переносное движение по отношению к осям O₁x₁y₁z₁).

Если провести плоскость Q перпендикулярную осям вращения Оz и O₁z₁, то в сечении твердого тела получим плоскую фигуру, которая  в относительном и переносном движениях будет оставаться в плоскости сечения. Это означает, что и в абсолютном движении плоская фигура остается в плоскости сечения.

Следовательно, результирующим (абсолютным) движением твердого тела будет плоское и характеризуется движением плоской фигуры в ее плоскости. Рассмотрим три случая.

Рис. 2.110

С л у ч а й   1. Переносное и относительное вращения направлены в одну сторону.

Изобразим сечение твердого тела плоскостью Q, перпендикулярной осям Oz и . Следы осей в сечении обозначим А и В (рис. 2.111).

Точка А плоской фигуры в относительном вращении имеет скорость равную 0,  в переносном

.

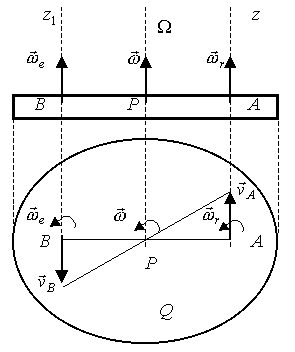
Рис. 2.111

Точка В плоской фигуры в переносном вращении имеет скорость равную 0, а в относительном

.

Векторы  и параллельны.

Мгновенный центр скоростей Р найдем на пересечении отрезков, соединяющих точки А и В и концы векторов скоростей этих точек.

Мгновенная ось абсолютного вращения  проходит через мгновенный центр скоростей Р.

Таким образом, мгновенная ось абсолютного вращения плоской фигуры лежит в плоскости, проходящей через оси переносного и относительного вращений, и,  будучи параллельной им, делит расстояние между этими осями на части, обратно пропорциональные угловым скоростям.

.

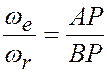Итак, если тело участвует одновременно в двух направленных в одну сторону вращениях вокруг параллельных осей, то результирующим (абсолютным) движением будет вращение вокруг мгновенной оси, параллельной данным, с  модулем абсолютной угловой скорости, равным сумме модулей угловых скоростей составляющих вращений.

.

С течением времени мгновенная ось меняет свое положение, описывая цилиндрическую поверхность. Положение мгновенной оси определяется соотношением

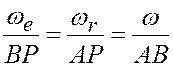, где ВР и  АР – расстояния от данных осей вращения до мгновенной;  АВ – расстояние между данными осями.

Задача 2.24. Кривошип О₁О (рис. 2.112) вращается вокруг неподвижной оси Oz против хода часовой стрелки с угловой скоростью  и заставляет подвижную шестерню 2 радиуса r₂ катиться по неподвижной шестерне 1 радиуса r₁. Определить абсолютную  и  относительную  угловые скорости шестерни 2.

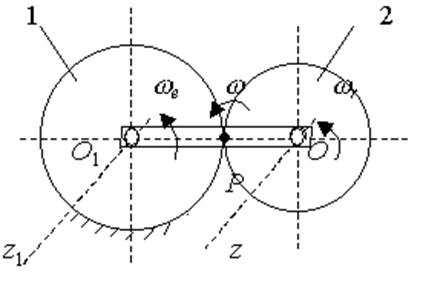
Рис. 2.112

Решение. Рассмотрим простейшую цилиндрическую планетарную передачу. Мгновенный центр скоростей шестерни 2 находится в точке касания шестерен. Для шестерни 2  вращение кривошипа является  переносным, угловая скорость - переносной, а ось  Oz₁ – осью переносного вращения. Ось относительного вращения шестерни 2 – Oz, мгновенная ось абсолютного вращения проходит через точку