Основные понятия и аксиомы статики. Материальная точка, аксиома инерции

Алгебраическая сумма моментов сил, действующих на левую или правую половину составной конструкции относительно точки С (внутреннего  шарнира), равняется нулю, т.е.

.

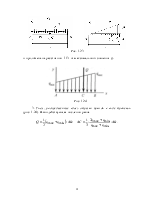
Задача 3. Однородные брусья АС и BD весом соответственно Р₁ и Р₂ расположены в вертикальной плоскости (рис. 3.1, а). Брусья свободно опираются друг на друга в точке С, а в точках А и В имеют неподвижные шарнирные опоры; в точке К брус BD закреплен невесомым стержнем.

Дано: Р₁= 10 Н, Р₂ = 20 Н, М₁ = 20 Нм, F= 50 Н,  l = 1 м, М₂ =  30 Нм.

Определить реакции связей в точках А, В, С и К.

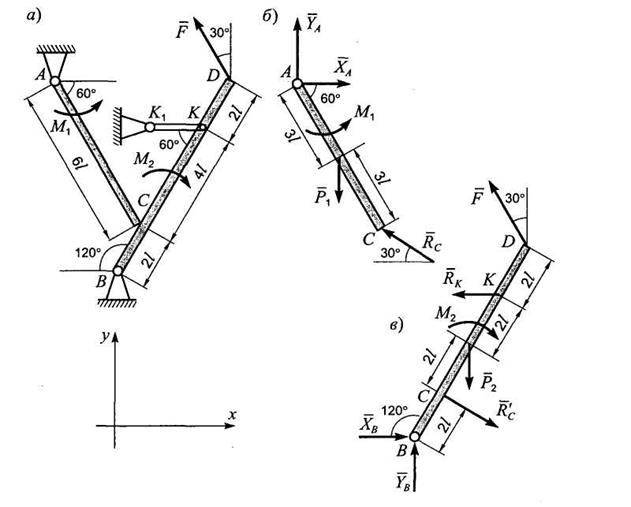
Рис. 3.1

Решение. Расчленим систему на две части и рассмотрим сначала равновесие бруса АС (рис. 3.1, б). Проведем координатные оси и изобразим действующие на брус АС силы: силу тяжести Р, пару сил с моментом М, реакции связей X_A,Y_A, R_e (реакцию неподвижной шарнирной опоры А изображаем двумя ее составляющими, реакция R_e направлена перпендикулярно брусу BD).

Для полученной плоской системы сил составим три уравнения равновесия:

,                      (3.1)

,                          (3.2)

.                (3.3)

Теперь рассмотрим равновесие бруса BD (рис. 3.1, в). На него действуют сила тяжести Р₂, сила F, реакции внешних связей  Х_В, Y_B, R_K и давление R’_С со стороны бруса АС, которое на основании равенства действия и противодействия направлено противоположно силе R_C.

Для полученной плоской системы сил тоже составим три уравнения равновесия:

                    (3.4)

                     (3.5)

       (3.6)

Решив систему уравнений (3.1) — (3.6) и учитывая при этом, что численно R'_C = R_C, найдем искомые реакции.

Ответ: Х_A=1,44 Н, Y_A=9,17 Н, Х_B = –26,06 Н, Y_B = –22,47 Н,  R_C = 1,66 H, R_K = –52,5 Н.  

Из полученных результатов видно, что силы Х_В, Y_B и R_K направлены противоположно показанным на рис. 3.1, в.

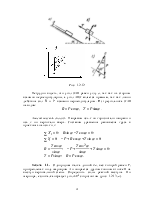
Задача 4. На угольник ABC (ABC = 90°), конец А которого жестко заделан, в точке С опирается стержень DE (рис. 3.2, а). Стержень имеет в точке D неподвижную шарнирную опору и к нему приложена пара с моментом М₂, а к угольнику — равномерно распределенная на участке KB нагрузка интенсивности q и пара с моментом М₁. Дано: M₁ = 10 кНм, q = 4 кН/м, а = 1 м, М₂ = 40 кНм. Определить реакции в точках А, С, D, вызванные заданными нагрузками.

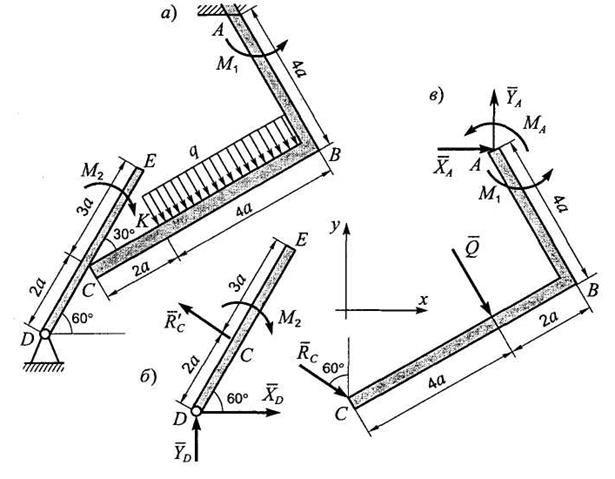
Рис. 3.2

Решение. Для определения реакций расчленим систему и рассмотрим сначала равновесие стержня DE (рис. 3.2, б). Проведем координатные оси и изобразим действующие на стержень силы и моменты: момент М₂, реакцию R^, направленную перпендикулярно стержню, и составляющие X_D и Y_D реакции шарнира D. Для полученной плоской системы сил составляем три уравнения равновесия:

                      (3.7)

                                  (3.8)

                                    (3.9)

Теперь рассмотрим равновесие угольника (рис. 3.2, в). На него действуют сила давления стержня R_С, направленная противоположно реакции R’_C, равномерно распределенная нагрузка, которую заменяем силой Q, приложенной в середине участка KB (численно Q = q∙4a= 16 кН), пара сил с моментом M₁ и реакция жесткой заделки, слагающаяся из силы, которую представим составляющими Х_А, YA, и пары с моментом М_А. Для этой плоской системы сил тоже составляем три уравнения равновесия:

                    (3.10)

                       (3.11)

(3.12)

Подставив в составленные уравнения числовые значения заданных величин и решив систему уравнений (3.7) — (3.12), найдем искомые реакции. При решении учитываем, что численно R’_C = R_C  в силу равенства действия и противодействия.

Ответ: R_C = 20 кН, Y_D = –10 кН, X_D= 17,34 кН, Х_А = –25,34 кН, Y_A = 23,87 кН,  М_А = –186,4 кНм.

Знаки указывают, что силы Y_D, X_A и момент М_А направлены противоположно показанным на рисунках.

Задача 5. Дана плоская составная конструкция с приложенными к ней нагрузками (рис. 3.3) Определить реакции шарниров А, В и С, если Р = 10 кН, q = 5 кН/м, М = 6 кНм, а = 1,2 м,  b = 1 м, r = = 0,15 м. Нить невесомая, трением в подшипнике блока D пренебречь.

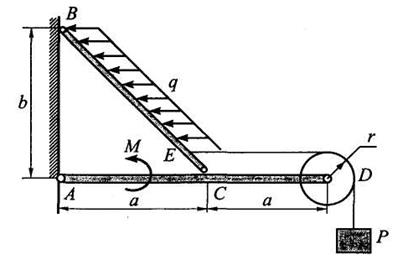
Рис. 3.3

Расчленим конструкцию на две части, освободив ее от шарниров А и В (внешние связи), шарнира С и горизонтальной нити (внутренние связи). Расчетные схемы изображены на рис. 3.4, а,б.

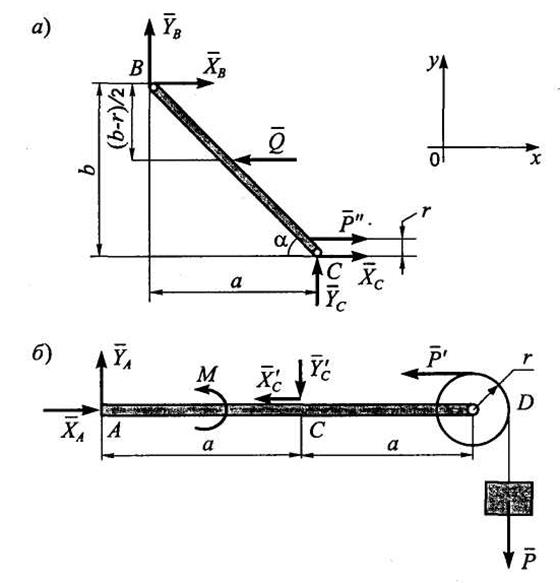
Рис. 3.4

На расчетных схемах обозначено:

X_A,Y_A - составляющие реакции шарнира А;

Х_В, Y_B - составляющие реакции шарнира В;

Х_С, Y_С - составляющие реакции шарнира С на балку