Если силы, действующие на систему, потенциальны, т.е. система консервативна, то обобщенная сила равна
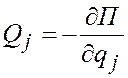 .
.
Тогда уравнение (3.45) примет вид
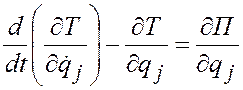 . (3.30)
. (3.30)
Задача 5. Исследование механической системы с применением уравнений Лагранжа второго рода
По условию задачи № 3 определить ускорение тела 1, используя уравнение Лагранжа П рода.
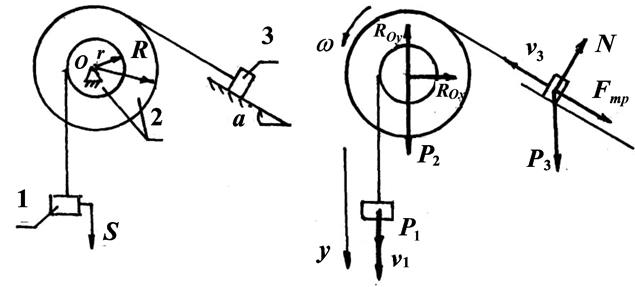
Решение.
1. Составление расчетной схемы.. На механическую
систему действуют
активные силы ![]() ,
, ![]() ,
, ![]() .
.
Применяя принцип освобождаемости от связей только к
внешним связям, покажем на расчетной схеме реакции шарнирно-неподвижной опоры ![]() и
и ![]() реакции
шероховатой поверхности
реакции
шероховатой поверхности ![]() и
и ![]() . Силу трения направим в сторону, противоположную
движению тела 3.
. Силу трения направим в сторону, противоположную
движению тела 3.
Изобразим скорости тел системы исходя из того, что тело 1 опускается.
2. Выбор теоремы.
Задачу решаем, используя дифференциальное уравнение механической системы в обобщенных координатах
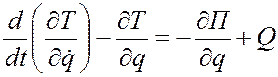 .
.
Так как система имеет одну степень свободы, а определяем ускорение тела 1, то за обобщенную координату примем координату первого тела у
q=y.
Обобщенная скорость, в таком
случае, ![]() .
.
3. Составление уравнения.
а) Определение кинетической энергии системы.
Кинетическая энергия системы представляет собой сумму кинетических энергий тел 1,2 и 3.
![]() .
.
Вычислим Q для неконсервативных сил
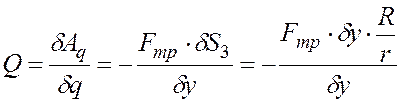 ,
,
то есть
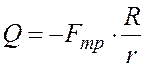 .
.
Работа сил ![]() и
и ![]() на заданном приращении обобщенной координаты
равна нулю, так как силы приложены к неподвижной точке. Работа нормальной
реакции поверхности N также равна нулю, сила перпендикулярна направлению
движения.
на заданном приращении обобщенной координаты
равна нулю, так как силы приложены к неподвижной точке. Работа нормальной
реакции поверхности N также равна нулю, сила перпендикулярна направлению
движения.
Подставим в обобщенную силу значения
![]() .
.
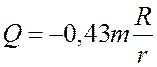 или
или ![]() .
.
в) Определение потенциальной энергии системы.
Потенциальная энергия численно равна работе потенциальных сил, действующих на систему, которую необходимо совершить, чтобы вернуть систему из отклоненного положения в положение равновесия.
![]() .
.
Высота,
на которую переместится точка приложения силы ![]() , равна
, равна
![]() .
.
В обобщенных координатах
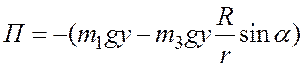 .
.
Подставляя числовые параметры, запишем
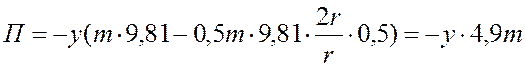 .
.
Подставляем значения Т, П и Q в уравнение Лагранжа П рода и преобразовываем
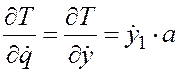 ,
,
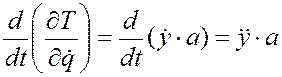 ,
,
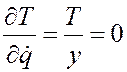 , так как Т не содержит у.
, так как Т не содержит у.
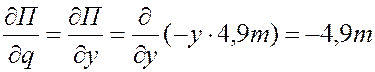 .
.
Таким образом, запишем
![]() ,
,
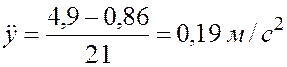
Значение ускорения тела получили со знаком «+». Это означает, что груз опускается ускоренно.
13.3. Кинетический потенциал и циклические координаты
Уравнение (3.30) можно преобразовать путем введения функции Лагранжа L=T- П, называемой кинетическим потенциалом.
Так как
![]() ,
,
![]() , то, кинетический потенциал
является функцией обобщенных координат, обобщенных скоростей и времени:
, то, кинетический потенциал
является функцией обобщенных координат, обобщенных скоростей и времени:
![]() .
.
Потенциальная энергия является функцией только обобщенных координат и времени, а потому
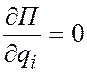 .
.
Пользуясь этим условием, получим:
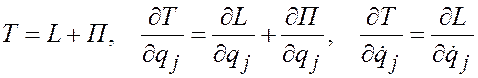 .
.
Подставимэти частные производные в уравнения Лагранжа (3.46):
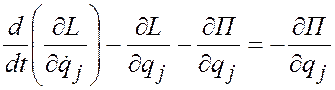
или
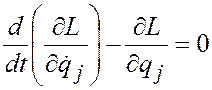 .
(3.31)
.
(3.31)
Уравнения (3.31) называются уравнениями Лагранжа второго рода для консервативной системы.
13.4. Последовательность решения задач на составление
уравнений Лагранжа
Последовательность составления уравнений Лагранжа:
1) определить число степеней свободы материальной системы;
2) выбрать систему координат и ввести независимые обобщенные координаты в числе, равном числу степеней свободы;
3) определить обобщенные силы системы ![]() ,
соответствующие избранным обобщенным координатам;
,
соответствующие избранным обобщенным координатам;
4) вычислить кинетическую энергию Т рассматриваемой системы материальных точек;
5) найти частные
производные от кинетической энергии по обобщенным скоростям ![]() , т.е.
, т.е. 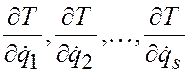 , а
затем вычислить производные от них по времени
, а
затем вычислить производные от них по времени
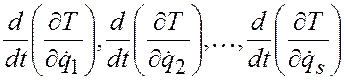 ;
;
6) определить
частные производные от кинетической энергии Т по обобщенным координатам:
![]() , т.е.
, т.е.
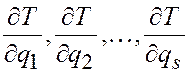 ;
;
7) полученные в пунктах 3,5 и 6 результаты подставить в уравнения Лагранжа.
Задача
3.26. Масса тележки 1 имеет ![]() , а масса находящегося
на ней сплошного цилиндрического катка 2 равна
, а масса находящегося
на ней сплошного цилиндрического катка 2 равна ![]() .
Определить, с каким ускорением будет двигаться тележка вдоль горизонтальной
плоскости под действием приложенной к ней силы
.
Определить, с каким ускорением будет двигаться тележка вдоль горизонтальной
плоскости под действием приложенной к ней силы ![]() (рис.
3.88), если каток при этом катится по тележке без скольжения. Массой колес
тележки пренебречь.
(рис.
3.88), если каток при этом катится по тележке без скольжения. Массой колес
тележки пренебречь.
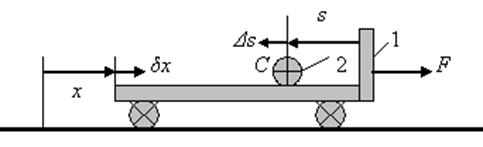
Решение. Система имеет две степени свободы (независимы перемещение катка относительно тележки и перемещение самой тележки). В качестве обобщенных координат выберем координату х тележки и координату s центра масс катка относительно тележки. Тогда уравнения Лагранжа для системы будут:
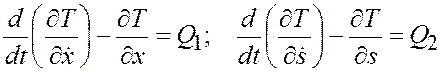 . (а)
. (а)
Кинетическая энергия тележки
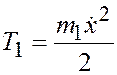
и катка
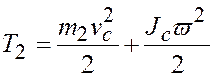 , где
, где ![]() -
абсолютная скорость центра С катка и численно
-
абсолютная скорость центра С катка и численно ![]() .
Так как для сплошного цилиндра
.
Так как для сплошного цилиндра
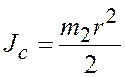 , а при качении без скольжения
, а при качении без скольжения
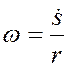 , где
s – относительная скорость центра С по отношению
к тележке (считать здесь
, где
s – относительная скорость центра С по отношению
к тележке (считать здесь ![]() было бы ошибкой), то
окончательно получим
было бы ошибкой), то
окончательно получим
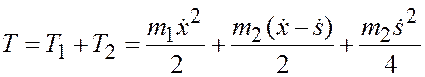 . (б)
. (б)
Тогда
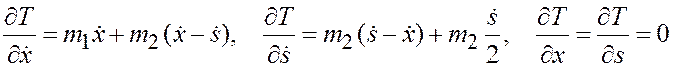 . (в)
. (в)
Для определения обобщенных сил дадим сначала системе возможное перемещение, при котором координата х получает приращение δх>0. На этом перемещении
![]() .
.
На перемещении же, при котором s
получает приращение δs, очевидно, ![]() . Следовательно,
. Следовательно,
![]() .
.
Подставляя
эти значения ![]() и
и ![]() и
значения производных, определяемые формулами (в), в равенстве (а), найдем
следующие дифференциальные уравнения движения системы:
и
значения производных, определяемые формулами (в), в равенстве (а), найдем
следующие дифференциальные уравнения движения системы:
![]() . (г)
. (г)
Из
последнего уравнения ![]() , тогда первое уравнение дает
окончательно для ускорения а1 тележки значение
, тогда первое уравнение дает
окончательно для ускорения а1 тележки значение
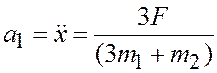 .
.
Если
каток был бы на тележке закреплен неподвижно, то ее ускорение, очевидно, равнялось
бы ![]() .
.
Отметим еще один результат. Допустим, что трения катка о тележку нет. Тогда он по тележке будет скользить, двигаясь поступательно, и
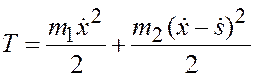 .
.
Легко видеть, что первое из уравнений (г) при этом не изменится, а второе, так как теперь
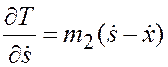
примет
вид ![]() и дает
и дает ![]() . В
результате из первого уравнения системы (г) находим для ускорения тележки
значение
. В
результате из первого уравнения системы (г) находим для ускорения тележки
значение
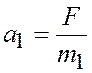 .
.
Объясняется такой результат тем, что при отсутствии трения тележка не увлекает с собой катка и движется так, как если бы катка на ней вообще не было.
13.5. Малые свободные колебания механической системы с одной степенью свободы
Состояние покоя (равновесия) механической системы может быть устойчивым, неустойчивым и безразличным (рис. 3.89). Состояние покоя механической системы называется устойчивым, если система, выведенная
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.