Исследование трехфазной цепи при соединении приемника треугольником

Точно так же замкнутый контур создается из трех фаз приемника.

Общие точки двух фаз источника и двух фаз приемника соединяются между собой линейными проводами. Так образуется связанная трехфазная трехпроводная система, в которой каждая обмотка источника соединена с соответствующей фазой приемника парой линейных проводов, каждый из которых обеспечивает такую связь в двух смежных фазах.

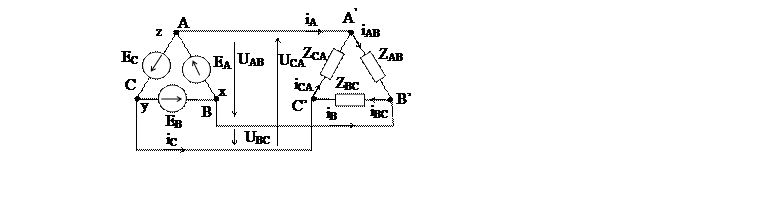
Рис. 1. Трехфазная система при соединении источника и приемника треугольником

Соединение нескольких обмоток источника в замкнутый контур возможно лишь в том случае, если сумма всех ЭДС этого контура равна нулю. Это требование выполняется при таком порядке соединения, когда конец предыдущей обмотки соединяется с началом следующей. Например конец х фазы А соединен с началом фазы В в общей точке хВ, конец y фазы В соединен с началом фазы С в общей точке yC и конец Zфазы С соединен с началом фазы А в общей точке zA.

Симметричная система ЭДС, действующих в контуре, имеет сумму равную нулю

.

В этом случае при холостом ходе источника ток в его обмотках отсутствует.

При несимметричной системе ЭДС их сумма не равна нулю, поэтому уже при холостом ходе в обмотках источника образуется ток, который может быть большим даже при малой несимметрии, так как сопротивления обмоток незначительно.

При неправильном включении обмоток, когда две соседние фазы соединены началами или концами, сумма ЭДС в контуре равна удвоенной величине ЭДС фазы.

Из схемы соединения треугольником видно, что фазные и линейные напряжения совпадают, так как конец одной фазы соединен с началом другой:    .

Каждая фаза приемника при соединении треугольником находится под линейным напряжением. Это обусловлено наличием в приемнике фазных токов i_AB, i_BC, i_CA, положительное направление которых на схеме выбрано соответственно положительному направлению ЭДС в фазах источника.

Точки А’, В’, С’ приемника , так же как и точки А, В, С источника, являются электрическими узлами, поэтому фазные токи отличаются от линейных i_A, i_B, i_C. Для узловых точек А, В, С можно написать уравнения в комплексной форме по первому закону Кирхгофа:

,

,

.

При симметричной нагрузке токи во всех фазах одинаковы.

Обозначив все фазные токи I_Ф, а линейные токи I_Л, получим общее соотношение между линейными и фазными токами в симметричной цепи:   .

Трехфазная цепь при соединении приемника треугольником и любой схеме соединения фаз источника имеет разветвленную многоконтурную схему. Расчет такой цепи выполняется одним из известных методов с учетом состава ее элементов и схемы соединения.

Расчет сложной цепи (рис. 1) значительно упрощается, если не принимать во внимание сопротивление проводов. В этом случае  напряжение на фазах приемника равны соответствующим напряжениям источника и, как правило, представляют собой симметричную систему.

Если трехфазная система напряжений, приложенных к приемнику, известна, то фазные токи в несимметричном приемнике определяются отдельно по формулам:

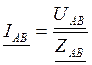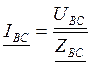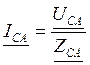,   ,   , где , ,  - полные сопротивления фаз.

Линейные токи находятся по формулам, записанным выше.

Векторная диаграмма этой цепи при активном сопротивлении нагрузки