Рабочая программа учебной дисциплины "Высшая математика". Организационно-методический раздел

1. Определения отображения множества А в множество В, множества А на множество В, взаимно однозначного отображения множества А на множество В. Примеры .
2. Определение эквивалентности двух множеств. Счетные множества, континуальные множества. Примеры.

Задания для самостоятельной работы

Решить задания 5-11 на стр. 12 учебного пособия [1]. На изучение раздела  отводится  два лекционных и два практических занятия.

Литература: [1] стр. 6-16

II .Векторная алгебра и аналитическая геометрия

1. Векторы. Проекция вектора на ось. Координаты вектора и точки. Направляющие косинусы и длина вектора. Линейные операции над векторами. Разложение вектора по ортонормированному базису.
2. Скалярное произведение векторов. Векторное произведение векторов. Свойства этих операций. Условие ортогональности и условие коллинеарности двух векторов.
3. Прямая линия на плоскости. Основная теорема. Различные формы уравнения прямой. Расстояние от точки до прямой. Угол между двумя прямыми.
4. Линии второго порядка: эллипс, гипербола, парабола. Преобразование координат (перенос начала)
5. Плоскость. Основная теорема. Уравнение плоскости. Расстояние от точки до плоскости. Прямая линия в пространстве.

Вопросы для самопроверки

1. Определение координат вектора. Формулы направляющих косинусов и длина вектора. Теорема о разложении вектора по ортонормированному базису. Сложение векторов, заданных координатами. Умножение вектора на число.

Литература [4] стр.121-128,134-141

2. Определение  скалярного произведения векторов. Свойства операции. Условие ортогональности двух векторов. Определении векторного произведения векторов. Свойства операций. Условия коллинеарности двух векторов.

Литература [4] стр.142-148, стр.148-157

3. Основная теорема о прямой на плоскости. Уравнение прямой с угловым коэффицентом, через две данные точки, уравнения пучка прямых. Формула расстояния от точки до прямой. Формула для тангенса угла от одной прямой до другой. Условие параллельности и перпендикулярности прямых.

Литература: [4] стр.52-58

4. Уравнения эллипса, гиперболы, параболы. Геометрический смысл параметров этих уравнений. Эксцентриситет эллипса и гиперболы.

Литература: [4] стр.70-76, 80-90, 94-97.

5. Основная теорема о плоскости. Уравнение плоскости, проходящей через данную точку и имеющей данный нормальный вектор. Формула расстояния от точки до плоскости. Теорема о задании прямой линии в пространстве. Канонические и параметрические уравнения прямой.

Литература: [4] стр.169-171, 181-185

Задания для самостоятельной работы

Рекомендуется решить задачи из сборника задач [6] :

1. №№ 763,764,769,773,751,753,777,782,783
2. №№ 814,820,826,835,842,843,851,857,859
3. №№ 224,226,227,236,245,255,267,314,322(2),320
4. №№ 444(5),445(3),449,465(5),466(1),515(3),516(3),518,520,532(1,2,3),595,596(1,3),

597(2),600,541(2),471(3)

5. №№ 919,930,932,940(2),941(1),942(3),960,964(1),1009(2),1019(2),1021,1039,1040(2),

1042,1050,1053

На изучение раздела отводится пять лекционных и пять практических занятий.

III  .Введение в математический анализ

1. Переменная величина. Область изменения переменной. Конечные и бесконечные промежутки. Функция, область ее определения, способы задания. Основные элементарные функции и их графики. Сложная функция. Элементарная функция.
2. Числовая последовательность. Монотонные и ограниченные  последовательности. Предел последовательности конечный и бесконечный. Теорема о существовании предела монотонной ограниченной последовательности (без доказательства). Предел последовательности Х_n=(1+1/n)ⁿ  .
3. Предел функции. Единственность предела. Свойства функции, имеющей предел: локальная ограниченность, устойчивость знака. Теорема о пределе функции, заключенной между двумя функциями, имеющими предел. Переход к пределу в неравенствах.
4. Бесконечно малые функции и их свойства. Теоремы об арифметических операциях над функциями, имеющими предел. Неопределенные выражения. Два замечательных предела. Сравнение бесконечно малых. Эквивалентные бесконечно малые функции, применение к вычислению пределов.
5. Непрерывность функции в точке. Непрерывность элементарных функций. Точки разрыва и их классификация. Свойства функций, непрерывных на отрезке. (формулировки теорем Вейерштрасса и Больцано-Коши)

Вопросы для самопроверки

1. Определение функции, способы задания функции. Перечислить основные элементарные функции и начертить их графики. Определение элементарной функции.

Литература: [1] стр.17-22

2. Определения числовой последовательности, монотонной последовательности, ограниченной последовательности. Определение предела последовательности конечного и бесконечного, символическая запись определений. Определения на геометрическом языке.Предел последовательности Х_n=(1+1/n)ⁿ  , число е.

Литература: [1] стр.23-29

3. Определение предела функции: limƒ(x) = A , в случае, когда а,А – числа. 

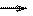                                                            x         а

Символическая запись определения.  Определения на геометрическом языке.             Распространение определения на случаи, когда А или а – символы +∞, -∞, ∞. Односторонние пределы функции. Перечислить свойства функции, имеющий предел.

Литература: [1] стр.29-32

4. Определение бесконечно малой функции. Перечислить свойства бесконечно малой функции. Сформулировать теоремы об арифметических операциях над функциями, имеющими предел. В каких случаях при вычислении предела функции имеется неопределенность? Перечислите известные виды неопределенностей и приемы их раскрытия. Запишите два замечательных предела. Какие виды неопределенностей они помогают раскрыть? Определения: функция α(x) бесконечно малая более высокого порядка, чем функция β(x) при x → а; α(x) и β(x)  – бесконечно малые функции одного порядка при  x → а  ; α(x) бесконечно малая n-ого порядка относительно β(x) привести примеры. Определение эквивалентных бесконечно малых функций. Сформулировать теоремы, при помощи которых эквивалентные бесконечно малые функции применяют к вычислению пределов. Запишите таблицу эквивалентных бесконечно малых функций.

Литература: [1] стр.33-46

5. Определения функции непрерывной в точке. Их эквивалентность. Односторонняя непрерывность функции в точке. Точки разрыва и их классификация. Примеры. Свойства непрерывных функций ( перечислить), теорема о непрерывности элементарной функции в каждой точке области определения. Определение функции непрерывной на отрезке. Сформулировать теоремы  Вейерштрасса и Больцано-Коши.

Литература: [1] стр.47-54

Задачи для самостоятельной работы:

1. Рекомендуется решить задачи из сборника задач [5]: №№ 9(б), 47(3,8,17,21), 54(2,12,15,16); из [7]: №№ 65-58.
2. Литература: [3], задачи №№61-71.
3. Литература: [3], задачи №№ 72-78; [5], №№ 272-276, 293-297, 299, 300, 314, 317, 319-325, 328, 329, 332, 335-337, 342; 381-384, 351-365.
4. Литература: [3], №№ 79-83.
5. Литература: [3], №№ 84-89; [5], №№225, 228, 230, 233, 234, 235, 236, 237, 240, 242.

На изучение раздела отводится шесть лекционных и шесть практических занятий.

IV. Дифференциальное исчисление функции одной переменной

1. Задачи, приводящие к понятию производной, её геометрический и механический смысл. Дифференцируемость и непрерывность. Производная суммы, произведения частного.
2. Производная сложной функции. Производная обратной функции. Производные основных элементарных функций.
3. Дифференцируемость и дифференциал функции. Геометрический смысл дифференциала. Инвариантность формы дифференциала первого порядка. Применение дифференциала в приближенных вычислениях.
4. Теоремы о среднем: Ферма, Роля, Лагранжа, Коши.
5. Производные и дифференциалы высших порядков. Раскрытие неопределенностей по правилам Лопиталя-Бернулли.
6. Формула Тейлора, Локальная формула. Формула с остаточным членом в форме Лагранжа.
7. Условия возрастания и убывания функции на промежутке. Экстремум функции. Необходимые условия экстремума. Достаточные условия существования экстремума.
8. Определение интервалов вогнутости вверх и вниз графика функции. Точки перегиба. Асимптоты. Схема исследования функции и построения её графика.   

Вопросы для самопроверки

1. Определение производной, её геометрический и механический смысл. Правила отыскания производной. Формулы отыскания производной.

Литература: [1], стр. 55-69

2. Определение дифференцируемости и дифференциала. Геометрический смысл дифференциала. Применение дифференциала в приближенных вычислениях.

Литература: [1], стр. 69-72

3. Теорема о среднем. Сформулировать теоремы Ферма, Роля, Лагранжа, Коши.

Литература: [1], стр. 72-78

4. Производные и дифференциалы высших порядков. Раскрытие неопределенностей по правилу Лопиталя-Бернулли: сформулировать теоремы.

Литература: [1], стр. 78-82

5. Многочлен Тейлора данной функции Локальная формула Тейлора. Формула Тейлора с остаточным членом в форме Лагранжа.

Литература: [1], стр. 83-88

6. Признаки вырастания и убывания функции. Определение точки максимума и точки минимума функции. Необходимые условия экстремума. Достаточные условия экстремума. 

Литература: [1], стр. 89-92

7. Определение интервалов вогнутости вверх и вниз графика функции. Точки перегиба. Асимптоты. Полное исследование функции и построение ее графика.

Литература: [1], стр. 93-98

Задания для самостоятельной работы

Рекомендуется решить задачи:

Литература: [5]

1.  №№ 466(1,5,12), 469, 477, 503, 504, 509, 524, 525, 534, 541, 544, 552, 555, 566, 569, 584, 587, 595, 617, 609, 622, 629, 652, 656, 658, 665, 814, 827, 829, 840.
2.  №№ 879, 883, 889(17,20), 900, 902.
3.  №№ 1118, 1120, 1129, 1131, 1320.
4.  №№ 1019, 1021, 1025, 1326, 1330, 1343, 1344, 1349, 1352, 1355, 13588, 1356, 1360.
5.  №№ 1499, 1503, 1505.
6.  №№ 1408, 1417. 

На изучение раздела отводится восемь лекционных и семь практических занятий.

V. Дифференциальное исчисление функции нескольких переменных

1. Понятие функции нескольких переменных. Множества точек на плоскости и в пространстве. n – мерное арифметическое пространство Rⁿ. Определение функции нескольких переменных. Предел. Непрерывность.
2. Частные производные. Дифференцируемость и дифференциал. Необходимые условия дифференцируемости. Производные от сложных функций. Инвариантность формы дифференциала первого порядка.
3. Частные производные и дифференциалы высших порядков.
4. Неявная функция и ее производная.
5. Экстремум функции нескольких переменных. Необходимые условия экстремума. Достаточные условия экстремума (формулировка теоремы).
6. Скалярное поле. Производная по направлению. Градиент. Поверхности и линии уровня.

Вопросы для самопроверки

1. Определения δ – окрестности точки на плоскости, в трехмерном, в n – мерном пространстве. Определения множества замкнутого, ограниченного, связного. Определения функции двух, трех, n переменных. Определение предела функции n переменных и непрерывности в данной точке.

Литература:  [1], стр. 99 – 105.

2. Частное и полное приращение функции двух переменных. Определение частных производных. Определение функции, дифференцируемой в данной точке и дифференциала. Необходимые условия дифференцируемости, достаточные условия дифференцируемости (формулировки теорем). Формула для отыскания производных от сложных функций двух переменных. Формула полной производной.

Литература: [1], стр. 105 – 110.

3. Частные производные и дифференциалы высших порядков.

Литература: [1], стр. 110 – 114.

4. Определение точки максимума и точки минимума функции двух переменных. Необходимые условия, достаточные условия экстремума.

Литература: [1], стр. 114 – 117.

5. Скалярное поле. Определение производной по направлению, формула для ее вычисления. Определение градиента функции. Поверхности и линии уровня.

Литература: [1], стр. 117 -119.

6. Неявная функция. Теорема о существовании и дифференцируемости неявной функции (формулировка)

Литература: [1], стр. 120 – 123.

Задания для самостоятельной работы

Рекомендуется решить следующие  задачи:

Литература: [5]

1.  №№  2986 – 2988, 3003, 3004, 3008, 3012, 3015 (1,2).
2.  №№  3037, 3040, 3041, 3043, 3045, 3047, 3046, 3055, 3056, 3061, 3101, 3104, 3110, 3113, 3115, 3125, 3127, 3128, 3131.
3.  №№  3181, 3182, 3184, 3186, 3219, 3225.
4.  №№ 3278,3276.
5.  №№  3451, 3455 (1,2), 3447, 3440 (3).
6.  №№  3147, 3154, 3155

На изучение раздела отводится четыре лекционных и пять практических занятий.

VI. Функции комплексного переменного

1. Комплексные числа. Их изображение на плоскости. Модуль и аргумент комплексного числа. Алгебраическая, тригонометрическая и показательная формы записи комплексного числа. Действия над комплексными числами. Формула Муавра.
2. Определение функции комплексного переменного. Комплексная функция действительного переменного. Показательная функция комплексного переменного и ее свойства