Задание 1.
Постановка задачи:
Уставный капитал = 105, количество акций =10, собственный капитал = 108, дивиденд =5, LIBOR = 2%
Оценить величину курса акций.
Принятые обозначения:
Div — дивиденд, руб
St — текущая рыночная цена
Vt — действительная стоимость акции
Решение задачи:
Действительную стоимость акции можно оценить из соотношения альтернативы положить эти деньги в банк: Vt=Div/LIBOR
Ответ:
Цена акций на рынке не должна быть меньше 250
Дополнительные пометки:
Текущую рыночную стоимость можно рассчитать более точно, введя параметры доходности или темпов роста дивиденда
Задание 2.
Постановка задачи:
Построить пример, когда облигация с номиналом 1000 стоит на рынке 1200
Принятые обозначения:
PM – рыночная цена облигации
N – номинал облигации
T – срочность облигации
LIBOR – межбанковская кредитная ставка
Inf – ставка инфляции
D – доходность облигации, D=N*g, g- процентная ставка купона
Идея решения:
Сначала строим обратную задачу, в которой рыночная стоимость считается известной, а за варьируемый параметр выбрана доходность. Затем, добавив в условие построенной модели найденную доходность и оставив прочие параметры, можно будет утверждать, что рыночная цена будет примерно равна 1200.
Предпосылки:
Ставки инфляции и LIBOR за время Т неизменны.
Под рыночной ценой понимается текущая стоимость облигации, или некоторая равновесная цена
Решение задачи:
Введем формулу для оценки рыночной стоимости:
РM= D*∑Tn=1(1-Inf/1+LIBOR)n + N*(1-Inf/1+LIBOR)T
Т.е сначала мы отдаем номинал облигации, затем получаем с этого доход (за два года ) и возвращенный номинал облигации с учетом инфляции и приведенные ко времени покупки облигации.
Зададим параметры модели:
PM =1200; N =1000; T = 2 года; LIBOR =10 %; Inf = 5%; D – ?
Подставив эти параметры в расчетную формулу, получим D≈282,78.
Ответ:
В модели неизменных за время Т ставок LIBOR и инфляции и при входных параметрах
N =1000; T = 2 года; LIBOR =10 %; Inf = 5%; g =28,28%
Рыночная цена облигаций составит 1200.
Примечания:
· Если не учитывать предпосылки, то расчетная формула изменится: Вместо ∑Tn=1(1-Inf/1+LIBOR)n будет ((1-Inf1/1+LIBOR1)+ (1-Inf1/1+LIBOR1)*(1-Inf2/1+LIBOR2)+…), где Inf1,2 – ставки инфляции (ожидаемые, модельные) за 1 и 2 года; LIBOR1,2- ставки LIBOR за 1 и 2 год
·
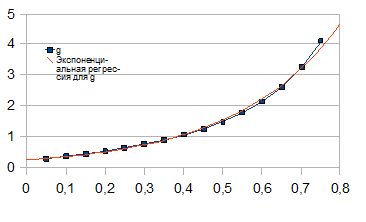 |
При 100% инфляции, необходим размер купон = ∞, что нереально. И данного графика (по оси абсцисс отложена инфляция, по оси ординат — величина купона где 1=100%) очевидно, что при увеличении инфляции при одной и той же LIBOR, доходность(купон) должна расти, чтобы на рынке за такую облигацию давали 1200.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.