Основные теоремы теории вероятностей. Теорема сложения вероятностей несовместимых событий

овощные консервы, причем первый завод поставляет продукции в три раза больше второго. Доля овощных консервов в продукции первого завода составляет 60%, а у второго 70%. Для контроля в магазине взято наугад одно изделие.

а) Какова вероятность того, что это окажутся мясные консервы?

б) Взятое изделие оказалось мясными консервами. Какова вероятность, что оно изготовлено вторым заводом?

Решение. Обозначим: событие А – взяты мясные консервы.

событие Н1 – изделие изготовлено I заводом.

событие Н2 – изделие изготовлено II заводом.

По условию задачи первый завод поставляет продукции в три раза больше, чем второй, то есть Р(Н1) > Р(Н2) в три раза.

или       Р(Н1) = 3× Р(Н2).

Отсюда имеем:

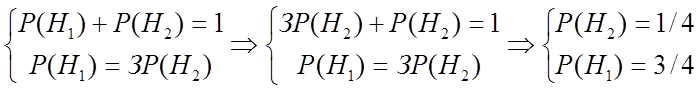
Вероятность того, что консервы мясные, для первого завода 40%, или   РН1 (А) = 0,4, для второго завода 30%, или   РН2 (А) = 0,3.

а) Учитывая, что событие А произойдет обязательно с одним из событий (гипотез) Н1, образующих полную группу, применяем формулу полной вероятности:

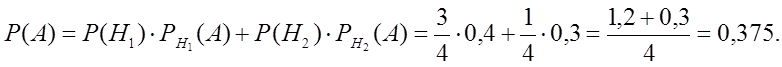
б) По условию событие А произошло, то есть взяты мясные консервы. Тогда вероятность гипотезы Н2 – консервы изготовлены вторым заводом - находим по формуле Байеса:

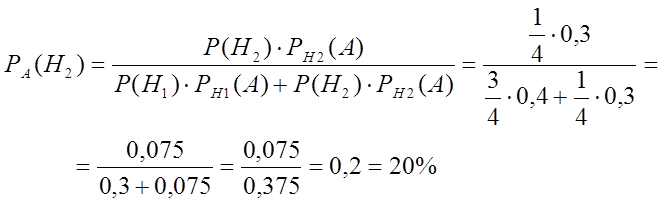
Замечание. Задача решается аналогично, если количество заводов будет три или более. Соответственно увеличится число слагаемых в формуле полной вероятности.

Задачи  21 - 30

Тема 4. Повторение независимых испытаний

Пусть известна вероятность появления события А в одном испытании:    Р(А) = р,  причем   р ¹ 0,   р ¹ 1,   тогда

 - вероятность непоявления события А.

Испытание повторяется n раз. Какова вероятность того, что событие А наступит при этом k раз?

Эта вероятность находится по формуле Бернулли:

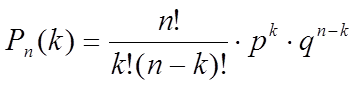, где   n! = 1 × 2 × 3 × …× n,   например,   5! = 1 × 2 × 3 × 4 × 5 = 120.

Напомним, что   0! = 1,   как и   1! = 1.

Формулу Бернулли удобно применять, если число повторных испытаний невелико (n £10).

Если число испытаний велико (n > 10), то вместо формулы Бернулли используется так называемая локальная формула Лапласа, которая является приближенной:

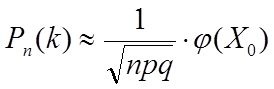,    где    .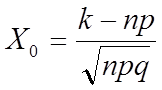

Значение функции j(х₀) берется по таблице (см. приложение 1).

Если число испытаний велико (n > 10) и нужно найти вероятность того, что при n испытаниях событие А наступит от k1 до k2 раза, то применяют интегральную формулу Лапласа, которая также является приближенной:

,       где   .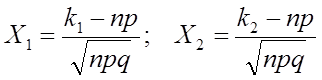

Значения функции Лапласа Ф(Х) берутся по таблице (приложение 2). В n повторных испытаниях событие А может наступить: 0; 1; 2; 3; …; n раз (то есть 0 £ k £ n). Для каждого из этих чисел можно найти соответствующую ему вероятность по формуле Бернулли.

То из чисел, которому соответствует самое большое значение вероятности, называется НАИВЕРОЯТНЕЙШИМ числом появления события А.

Наивероятнейшее число k0 находится как целое число из промежутка:

,

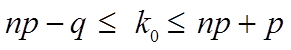k0 может принимать либо одно значение, либо два соседних целых значения, когда вероятности их одинаковы.

Вероятность Р_n(k_о), соответствующую значению k = k0, находим либо по формуле Бернулли, при n £ 10, либо по локальной формуле Лапласа, при n > 10.

Вероятность появления события хотя бы один раз в n испытаниях находится с помощью противоположного события:

Рn (событие наступит хотя бы один раз) = 1 – Рn (ни разу) =

= .

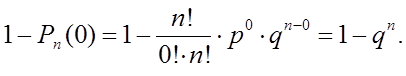Задача. Стрелок поражает цель с вероятностью 0,7.

1)  С какой вероятностью в серии из 5 выстрелов он поразит мишень:

а) ровно два раза;

б) хотя бы один раз;

в) не менее четырех раз.

г) каково наивероятнейшее число попаданий и соответствующая ему вероятность?

2) Стрелком при тех же условиях совершается серия из 20 выстрелов.

а) Чему равна вероятность того, что попаданий будет ровно половина?

б) Найти вероятность того, что число попаданий будет не менее 12 и не более 18?

Решение. По условию задачи: р = 0,7;   n = 5;   k = 2;   m = 4;

         N = 20;   k1 = 12;   k2 = 18.

Вероятность промаха   q = 1 - р  =  1 - 0,7  =  0,3.

а) Вероятность попадания ровно два раза в серии из пять выстрелов находим по формуле Бернулли, так как число испытаний n = 5 невелико (n £ 10):

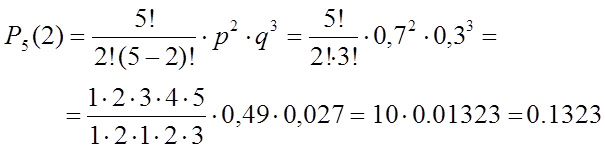
б) Событию D – «стрелок поразит мишень хотя бы 1 раз», противоположно событие  - «не поразит ни разу», то есть стрелок промахнется все пять раз, следовательно, число попаданий   k = 0:

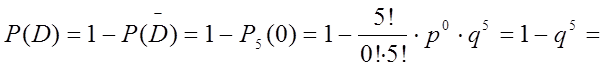
Здесь учтено, что   0! = 1  и  .

в) Событие «стрелок поразит мишень не менее четырех раз» запишем в виде: m ³ 4, тогда

Здесь применена теорема сложения вероятностей несовместимых событий. Используя формулу Бернулли, найдем:

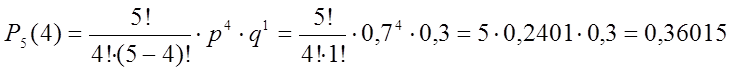
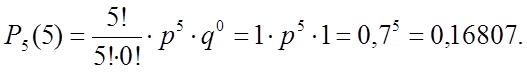
г) Наивероятнейшее число попаданий kо находим как целое число из промежутка

nр – q £ k_о £ nр + р

5× 0,7 – 0,3 £k_о £ 5× 0,7 + 0,7

3,2 £ k_о £4,2

Очевидно, что k_о = 4.

Соответствующая ему вероятность  находится по формуле Бернулли. В данной задаче она уже была найдена выше:

.

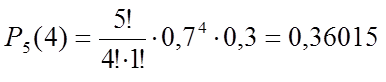2)  В этой задаче число испытаний N = 20 достаточно велико

(N > 10), поэтому используем приближенные формулы Лапласа.

а) Число попаданий ровно половине из 20, то есть 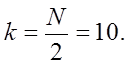 Соответствующую вероятность находим по локальной формуле Лапласа.

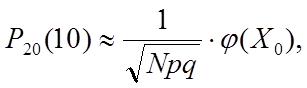        где

.

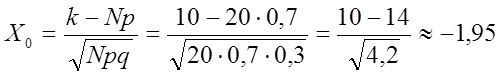Результат вычислений для Хо округляем с точностью до 0,01, так как значения функции j(х) табулируются в приложении 1 с таким шагом для   х.

По таблице приложения 1, учитывая четность функции j(х), находим:

.

Тогда .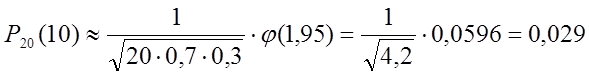

б) Вероятность того, что число попаданий будет не менее 12 и не более 18, вычисляем по интегральной формуле Лапласа:

, где

.

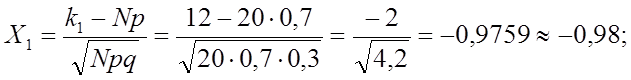
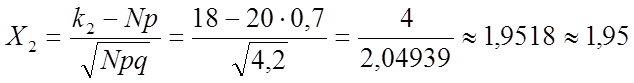Значения для Х1 и Х2 округляем до 0,01, так как таблица значений функции Лапласа Ф(Х) предусматривает такую точность для Х. По таблице приложения 2, учитывая нечетность функции Ф(Х), находим:   Ф(-0,98) = -Ф(0,98) = -0,3365;    Ф(1,95) = 0,4744.

Тогда Р20(12;18) = Ф(1,95) – Ф(-0,98) = 0,4744 + 0,3365 = 0,8109.

Ответ: 1) а) 0,1323;   б) 0,99757;   в) 0,52822;   г) k₀ = 4; 0,36015;

2) а) 0,0291;   б) 0,8109.

Задачи  31 - 40

Тема 5. Случайные величины

Случайной величиной называется переменная, принимающая свои возможные числовые значения с определенной вероятностью.

Например:  Х- балл, полученный на экзамене;

Y – число студентов, явившихся на лекцию;

Z – величина выигрыша в лотерее;

U – рост человека и т.п.

Виды случайных величин: 1) непрерывная;

2) дискретная.

Непрерывная случайная величина принимает сплошь все значения из некоторого промежутка.

Дискретная случайная величина Х принимает лишь отдельные значения. Закон распределения дискретной случайной величины записывается в виде таблицы, где перечислены все значения случайной величины Х и соответствующие им вероятности:

Х	х1	х2	х3	…	хn
Р(х)	р1	р2	р3	…	рn

Следует иметь в виду, что всегда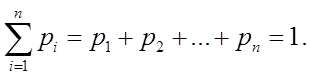

Основные числовые характеристики дискретной случайной величины:

1) Математическое ожидание (ожидаемое среднее значение случайной величины)

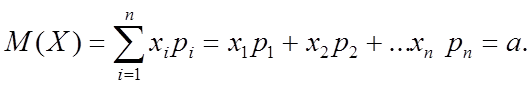
2)Дисперсия (мера рассеяния значений Х от среднего значения а):

.

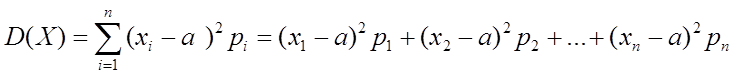3) Среднее квадратичное отклонение (характеристика рассеяния в единицах признака Х):

Второй способ вычисления дисперсии:

       где

.

Пример. Найти: а) математическое ожидание; б) дисперсию;

в) среднее квадратичное отклонение дискретной случайной величины по данному закону ее распределения, заданному в виде таблицы.

Хi	0	1	3	4	8	9
Рi	0,06	0,04	0,24	0,16	0,3	0,2

Решение. Заметим, что  

.

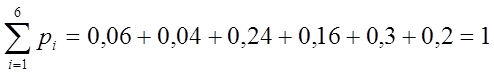а) Математическое ожидание: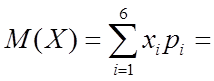   

=

б) Дисперсию случайной величины найдем двумя способами:

1) 

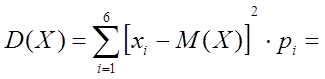
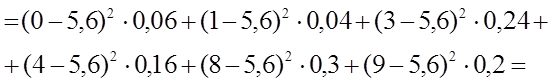
2)

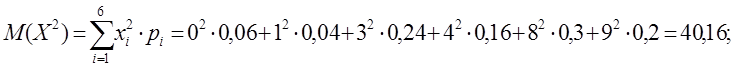
Тогда

в) Среднее квадратичное отклонение:

В приведенном выше примере закон распределения случайной величины Х был задан. Рассмотрим задачу, когда нужно составить закон распределения дискретной случайной величины Х. Для этого часто используют теоремы теории вероятностей.

Задача. У пользователя имеются четыре электрических лампочки, каждая из которых может оказаться бракованной с вероятностью 0,3. Пользователь ввинчивает лампочки по одной до загорания лампочки. Случайная величина Х – количество использованных лампочек. Составить закон распределения случайной величины Х и найти его основные характеристики: математическое ожидание, дисперсию и среднее квадратическое отклонение.

Решение. Очевидно, что число ввинченных лампочек Х может оказаться равным 1; 2; 3 и 4.

Обозначим: событие    А_n – лампочка n-ая по счету загорелась;

- лампочка n-ая по счету не загорелась.

События А1, А2, А3, А4 – независимые.

По условию   Р(А_n) = 0,7;     Р() = 0,3.

Х = 1, ввинченная лампочка будет всего одна, если загорится первая же лампочка:

p₁ = Р(Х = 1) = Р(А1) = 0,7.

Х = 2, ввинченных лампочек окажется две, если первая лампочка