
















































Мальчик: Я думаю, что на левом рисунке все точки, которые отмечены на замкнутой линии, находятся на одинаковом расстоянии от точки О, а на правом - это условие не выполняется.
Проверь! Прав ли мальчик?
Поставь на линии слева ещё 4 точки. На каком расстоянии от точки О они будут находиться?
Замкнутая кривая слева – окружность.
С помощью какого инструмента можно провести окружность?
№ 450 (с.157)
Выбери рисунок, на котором все точки линии находятся на одинаковом расстоянии от точки О. Как называется такая линия?
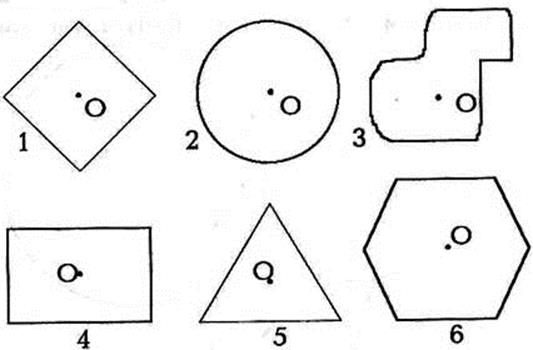
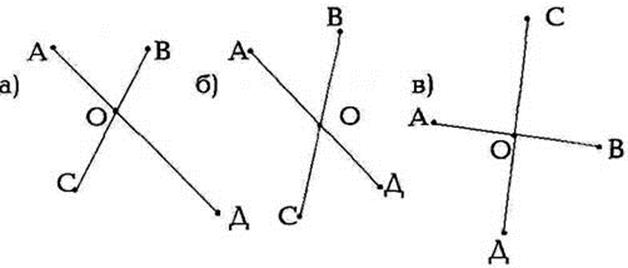
№ 451 (с.158)
Можно ли провести окружность с центром в точке О так, чтобы она проходила через точки А, В, С, Д:
№ 452 (с.158) Какие точки лежат на окружностях:
а) с центром в точке О и с центром в точке М?
б) с центром в точке М и с центром в точке К?
№ 453 (с.159) Наложи на страницу учебника прозрачный лист бумаги и обведи на нём замкнутую кривую линию.
Проверь! Можно ли назвать эту линию окружностью? Вырежи фигуру, ограниченную кривой линией.
R У тебя получился круг.
Если соединить любую точку окружности с ее центром, то получится отрезок, который называется радиусом окружности или радиусом круга (R).
Попробуй построить окружность, у которой:
а) R = 4 см, б)R = 3 см.
№ 454 (с.159) Подумай, можно ли провести пять осей симметрии в круге. Как это проверить?
3 класс.
Продолжается работа, связанная с изучением геометрических фигур и с развитием пространственного мышления, Пользуясь инструментами (линейка, циркуль, угольник) дети решают задачи на построение симметричных точек относительно данной прямой. Задания на симметричные фигуры, ось симметрии, построение симметричных фигур относительно данной прямой с помощью инструментов.
Уроки по данной теме можно начать с задания №552 (с. 165).
«Наложи прозрачную бумагу на страницу учебника, переведи на нее эти фигуры и вырежи их.
|
|
Можно ли утверждать, что эти фигуры симметричные? Как можно это проверить? Сколько осей симметрии в каждой фигуре?»
А лучше предложить учащимся просмотреть учебник и найти в нем рисунки с симметричными фигурами.
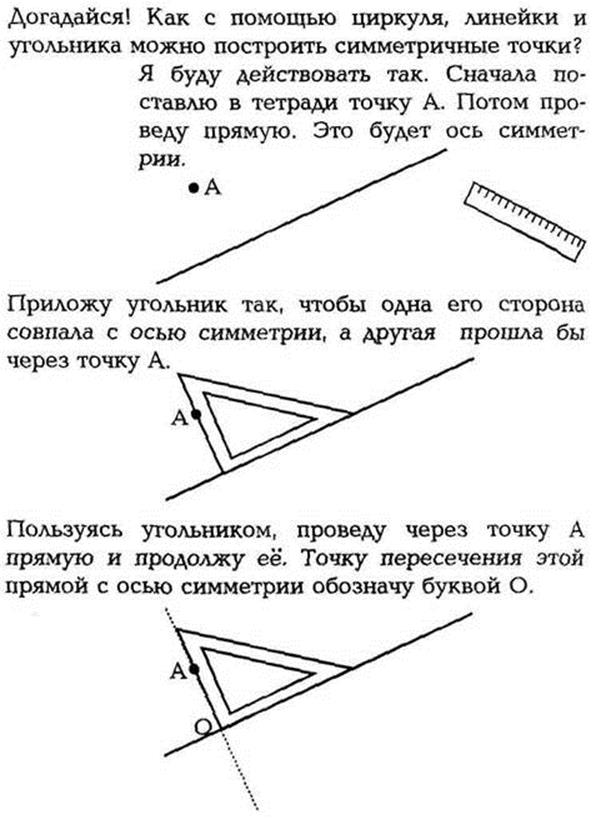
№553 (с. 166)
|
|
Перед классом ставит вопрос: «Кто догадается, как с помощью циркуля, линейки и угольника построить точку, симметричную данной, если прямая - ось симметрии?» Дети высказывают свои предложения, желающие пробуют выполнить построение на доске, все остальные наблюдают. Не следует жалеть времени на этот поиск.
В зависимости от действий учеников учитель строит дальнейшую работу по – разному:
- он может сам выполнить одну операцию, а ребятам предложить действовать дальше;
- один ученик будет читать в учебнике о действиях Миши, а остальные попробуют выполнить самостоятельно построение симметричной точки в тетрадях (без образца на доске!);
- школьники сначала прочитают текст в учебнике, затем попытаются самостоятельно воспроизвести описанные там действия в тетради. Возможен и такой вариант. Учитель показывает классу лист, на котором нарисованы прямая и точки: Красная (К), синяя (С), зеленая (З). Говорит: «Маша утверждает, что точки К и С симметричны, Миша - что точки К и З симметричны. Как это проверить?»
Дети складывают лист по прямой, прокалывают его там, где нарисована точка К, и убеждаются в том, что одновременно прокол попадает на точку З. Учитель может соединить точки К и З и приложить к прямой линии угольник.
Анализ этой ситуации поможет высказать ребятам догадку о построении симметричных точек относительно данной прямой. Организуя эту работу, следует иметь в виду, что задача учителя заключается не в том, чтобы учащиеся скопировали образец его действий и построили симметричную точку, а в том, чтобы они:
- проявляли сообразительность;
- учились самостоятельно осмысливать информацию, данную в учебнике;
- овладевали умением пользоваться инструментами для решения конкретной задачи;
- использовали представления о симметричных фигурах.
4 класс.
В четвертом классе, а именно в третьей четверти, повторяются и отрабатываются знания, умения, навыки о геометрических преобразованиях. Учащиеся вспоминают, как с помощью циркуля и угольника построить точку или фигуру, симметричную относительно данной прямой.
Так же вводятся в активное пользование стереометрические фигуры. Дети активно работают с понятиями: вершина, грань, ребро. Пространственное мышление развивается также при работе с развёртками стереометрических фигур.
№60 (с.28)
Выбери куб, который можно сделать из данной развёртки.
|
|
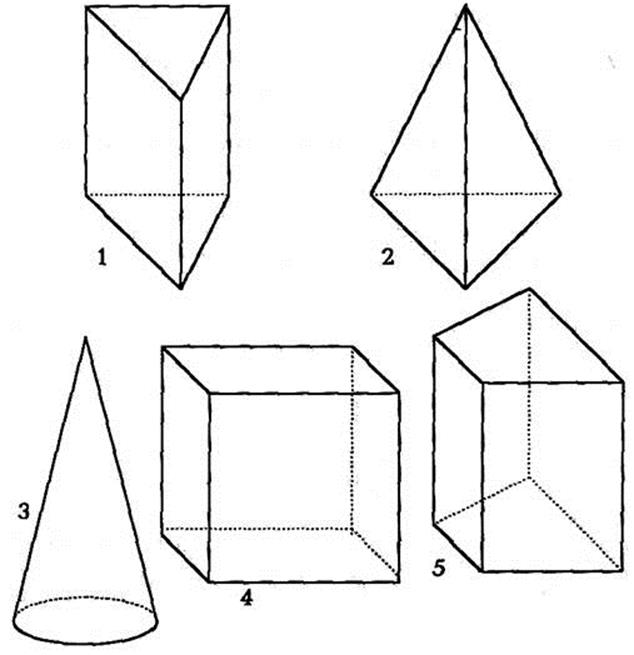
№ 6 (с.6)
Догадайся!
а) Какая фигура "лишняя"?
б) У какой фигуры 6 вершин, 5 граней, 9 рёбер?
в) У какой фигуры только одна вершина?
г) В чём сходство и различие фигур 4 и 5?
д) Названия каких из этих фигур ты знаешь?
Проанализировав все четыре учебника Н. Б. Истоминой, мы видим, что в основе методики формирования геометрических представлений лежит активное использование приемов умственной деятельности, нацеленность на развитие пространственного мышления и установления соответствия между моделями геометрических
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.