Глава 20. Метод прямой капитализации дохода в двухскоростной модели DDM и CAPM
Исследуется уравнение для неизвестной ставки капитализации дохода полученное в главе 20 для смешанной неравновесной модели DDM и CAPM. На основе принципа сжимающих отображений получены условия существования и единственности решения. Предложен численный алгоритм метода последовательных приближений. Рассматривается числовой пример.
В главах 19 и 20 нами изучалась смешанная модель DDM и CAPM для оценки рисковой ставки дисконта. В частности, в главе 20 было получено следующее уравнение для определения текущей обменной стоимости актива:
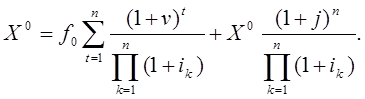 (20.1)
(20.1)
Здесь n –– предполагаемая длительность холдингового периода;
![]() неизвестная
текущая обменная стоимость актива;
неизвестная
текущая обменная стоимость актива;
![]() известное начальное значение чистого дохода (для
оценки бизнеса –– денежного потока);
известное начальное значение чистого дохода (для
оценки бизнеса –– денежного потока);
![]() среднее значение скорости изменения чистого
дохода;
среднее значение скорости изменения чистого
дохода;
![]() подходящая
ставка дисконта;
подходящая
ставка дисконта;
![]() среднее
значение скорости изменения обменной стоимости актива.
среднее
значение скорости изменения обменной стоимости актива.
В рамках двухскоростной модели DDM и CAPM в главе 20 было показано, что подходящая ставка дисконта задается формулой:
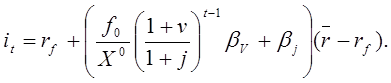 (20.2)
(20.2)
Здесь![]() средняя доходность
рыночного портфеля;
средняя доходность
рыночного портфеля;
r–– случайная доходность рыночного портфеля;
![]() дисперсия r;
дисперсия r;
![]() безрисковая ставка дохода,
безрисковая ставка дохода,
![]() ковариация с.в.
ковариация с.в. ![]()
νt, jt –– случайные скорости изменения чистого дохода ![]() и сравнительной стоимости актива
и сравнительной стоимости актива ![]() соответственно за t-й период:
соответственно за t-й период:
![]() .
.
Коэффициенты бета скорости изменения дохода и стоимости определяются формулами
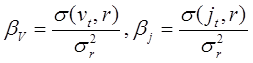 . (20.3)
. (20.3)
Предположим, что последовательности ![]() представляют собой последовательности
независимых одинаково распределенных с.в. (как в модели Блэка-Шоулза) и,
следовательно, стационарны в узком смысле. Отсюда следует в частности, что
коэффициенты бета в (20.3) не зависят от t. В главе
20 уравнение (20.1) использовалось для оценки инвестиционной стоимости актива.
Неизвестная стоимость в обмене заменялась на стоимость замещения, известную из
затратного подхода. При этом уравнение (20.1), вообще говоря, нарушается, но
правая часть представляет оценку инвестиционной стоимости. В настоящей работе
уравнение (20.1) исследуется относительно неизвестной стоимости в обмене
представляют собой последовательности
независимых одинаково распределенных с.в. (как в модели Блэка-Шоулза) и,
следовательно, стационарны в узком смысле. Отсюда следует в частности, что
коэффициенты бета в (20.3) не зависят от t. В главе
20 уравнение (20.1) использовалось для оценки инвестиционной стоимости актива.
Неизвестная стоимость в обмене заменялась на стоимость замещения, известную из
затратного подхода. При этом уравнение (20.1), вообще говоря, нарушается, но
правая часть представляет оценку инвестиционной стоимости. В настоящей работе
уравнение (20.1) исследуется относительно неизвестной стоимости в обмене ![]() актива.
актива.
20.1. Уравнение для ставки капитализации
Обозначим через ![]() неизвестную
ставку капитализации. Тогда ставка дисконта (20.2) является линейной функцией
ставки капитализации:
неизвестную
ставку капитализации. Тогда ставка дисконта (20.2) является линейной функцией
ставки капитализации:
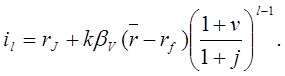 (20.4)
(20.4)
Здесь через ![]() обозначена для
краткости рисковая ставка дисконта отвечающая формально
обозначена для
краткости рисковая ставка дисконта отвечающая формально ![]() в
соответствии с моделью CAPM:
в
соответствии с моделью CAPM:
![]() (20.5)
(20.5)
Предполагается, что
![]() (20.6)
(20.6)
Деля обе части (20.1) на ![]() и
подставляя в него (20.4) после преобразования получим, что оно может быть
записано в виде:
и
подставляя в него (20.4) после преобразования получим, что оно может быть
записано в виде:
![]() (20.7)
(20.7)
где
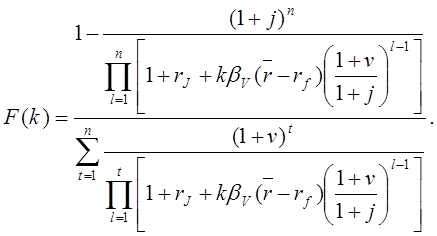 (20.8)
(20.8)
Экономический смысл имеют неотрицательные ставки капитализации. Поэтому следует исследовать решение (20.7),(20.8) при
![]() (20.9)
(20.9)
20.2. Свойства функции F(x)
При k=0 получим в частности известную формулу для ставки капитализации в двухскоростной детерминированной модели (см. гл.16):
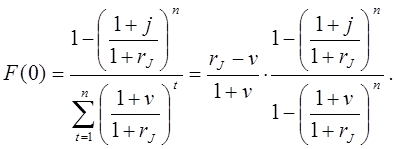
В частности, при ![]() получим
формулу Гордона
получим
формулу Гордона
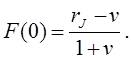
Предполагается, что
![]() (20.10)
(20.10)
В этом случае
![]() (20.11)
(20.11)
Нетрудно видеть, что функция F(k) является монотонной по k. При ![]() она возрастает, а при
она возрастает, а при ![]() –– убывает. При
–– убывает. При ![]() значение
функции совпадает с F(0).
значение
функции совпадает с F(0).
20.3. Существование и единственность решения
Рассмотрим отдельно два случая.
Пусть![]() . В
этом случае
. В
этом случае ![]() и в силу (20.11) функция F
отображает интервал
и в силу (20.11) функция F
отображает интервал ![]() в себя. Множество
в себя. Множество ![]() представляет собой полное метрическое
пространство с евклидовой метрикой
представляет собой полное метрическое
пространство с евклидовой метрикой
![]()
Поэтому согласно принципу сжимающих отображений для существования и единственности решения уравнения (20.7) достаточно сжимаемости отображения F(.). Последнее в силу дифференцируемости F(.) равносильно условию:
![]() (20.12)
(20.12)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.