Исследование понижающего преобразователя постоянного тока (DC-DC Buck Converter), страница 2

Выбор частоты среза f_c. Частота среза f_c должна быть больше резонансной частоты f_LC LC-контура. В данном примере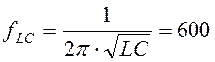Гц. Поэтому выберем f_c = 1000 Гц. С помощью MATLAB-скрипта (листинг 2.1) можно получить диаграмму Боде силового каскада G_PS(s) и определить, что

  дБ;  (рис. 2.9).

Листинг 2.1

L=100e-6;

C=697e-6;

rc=0.1;

Vin=30;

R=4;

Gps=(Vin/(L*C))*tf([rc*C 1],[1 (1/(C*R)+rc/L) 1/(L*C)]);

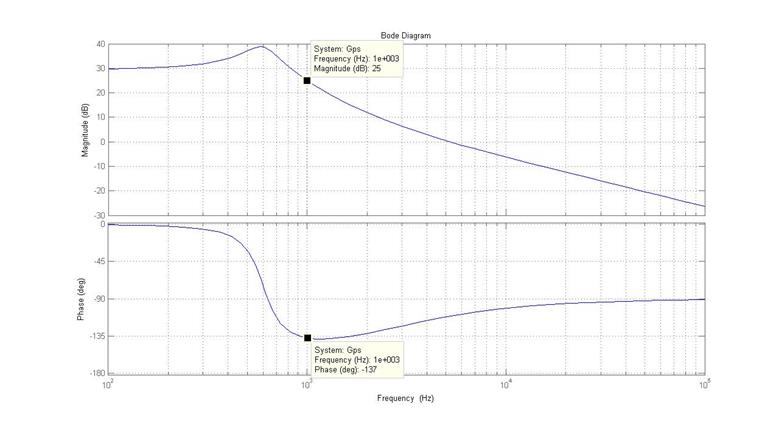
Рис. 2.9. Диаграмма Боде силового каскада

В качестве передаточной функции регулятора выберем следующую передаточную функцию:

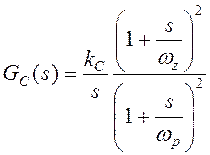,                                           (2.2)

где w_p > w_z.

Диаграмма Боде передаточной функции (2.2) приведена на рис. 2.10.

Для обеспечения нулевой установившейся ошибки передаточная функция G_С(s)  содержит полюс 1/s. Это определяет начальный сдвиг фазы контурной передаточной функции G_L(s), который равен -90°. Выбор же частоты среза f_c больше резонансной  f_LC гарантирует, что функция G_PS(s) на частоте f_c будет иметь максимальный фазовый сдвиг (в данном примере ).

Таким образом, сумма фазового сдвига -90°, вызванного наличием интегратора 1/s, и  будет меньше -180°:

.

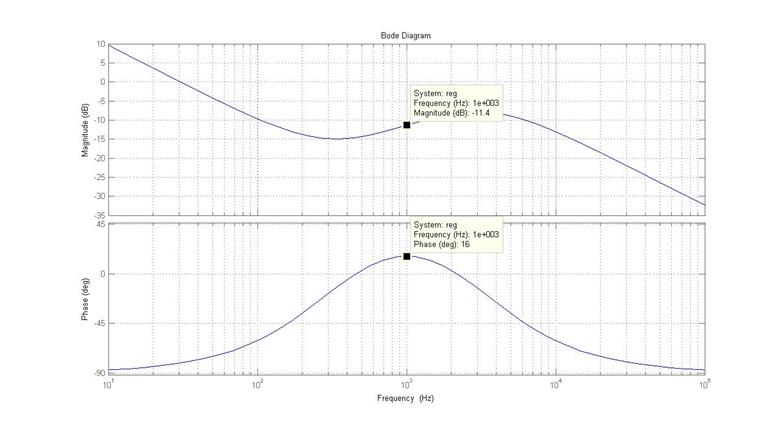
Рис. 2.10. Диаграмма Боде регулятора

Поэтому для получения запаса по фазе 60° необходимо увеличить фазу на частоте среза f_c  болем, чем на 90°, путем добавления двух совпадающих нулей на частоте f_z, чтобы устранить влияние двух полюсов в передаточной функции G_PS(s).

Для резкого спада ЛАЧХ перед частотой переключения f_s и для физической реализуемости регулятора в передаточную функцию G_С(s) добавлены два полюса на частоте f_p (f_p > f_z).

Коэффициент регулятора k_C выбирается таким образом, чтобы контурный коэффициент усиления на частоте среза был равен единице.

Расчет необходимого увеличения фазы.  Запас по фазе определен на уровне j_PM=60°. Необходимое увеличение фазы j_boost на частоте среза рассчитывается исходя из того, что передаточные функции G_PWM(s) и k_FB не вносят в контур никакого фазового сдвига:

.                               (2.3)

Для желаемой передаточной функции G_L(s) имеем:

.                                      (2.4)

Регулятор на частоте среза должен обеспечить повышение фазы на j_boost, т.е.

.                                      (2.5)

Используя выражения (2.3)-(2.5) получим требуемое повышение фазы:

.

Для рассматриваемого примера , поэтому

.

Расчет коэффициента k_C на частоте среза.

На частоте среза выполняется равенство:

.

В данном примере çG_PWM(s) ç=1;  дБ = 18.2;  k_FB = 0.2.

Тогда..

Для регулятора с передаточной функцией (2.2) повышение фазы j_boost достигает своего максимума на средней геометрической частоте . Для подходящего выбора параметров регулятора частоту среза f_s приравнивают к средне геометрической частоте.

Введем в рассмотрение коэффициент K_boost, который связывает повышение фазы и  геометрическое расположение нулей и полюсов регулятора:

.

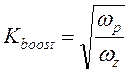Связь между K_boost и j_boost дается выражением:

.

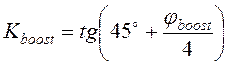В терминах коэффициента K_boost параметры регулятора могут быть рассчитаны следующим образом:

;

;

.

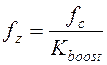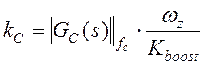Схемная реализация регулятора (2.2) приведена на рис. 2.11.

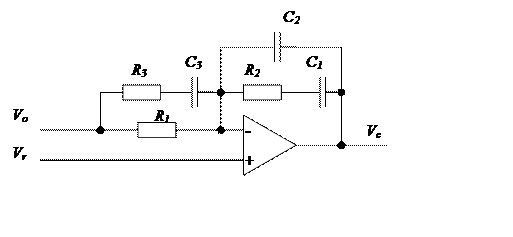
Рис. 2.11. Реализация регулятора на ОУ

Резистор R₁ выбирается с учетом нагрузочной способности датчика выходного напряжения преобразователя (делителя). Остальные параметры вычисляются по формулам:

;

;

;

;

.

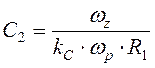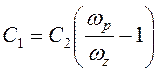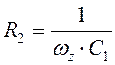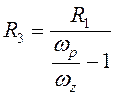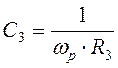Для рассматриваемого примера:

С₁=46.75 нФ; С₂=5.8 нФ; С₃=4.22 нФ; R₁=100 кОм; R₂=10.1 кОм; R₃=12.6 кОм; f_z=334 Гц; f_p=2.988 кГц.

Изучение работы замкнутой системы производится с помощью принципиальной схемы на рис. 2.12.

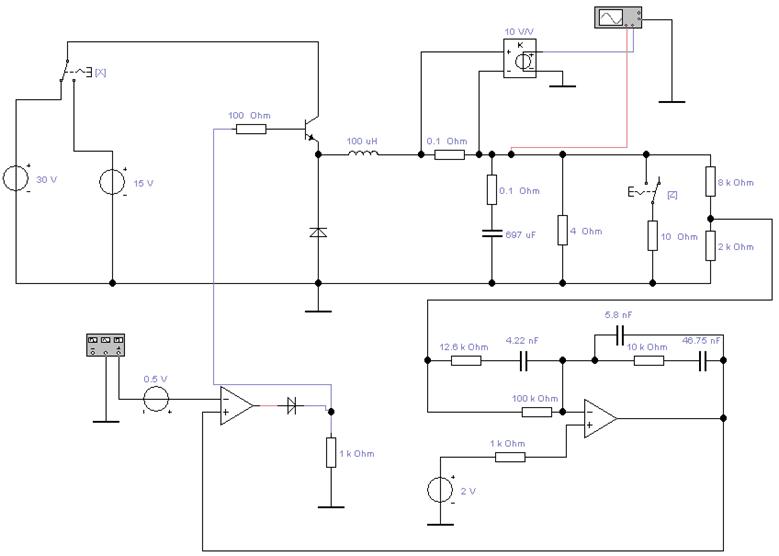
Рис. 2.12. Принципиальная схема преобразователя с регулятором

Выходное напряжение преобразователя V_o=2В/k_FB=2/0.2=10 В.

На рис. 2.13 изображены переходные процессы при изменении нагрузки преобразователя.

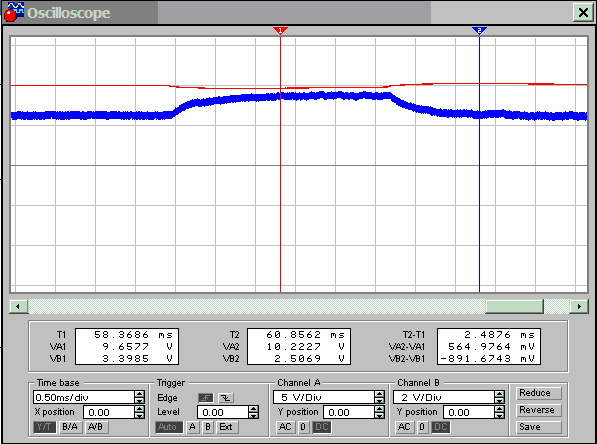
Рис. 2.13. Осциллограммы выходного напряжения преобразователя
 (красная линия) и тока через индуктивность (синяя линия) при набросе и сбросе нагрузки

Контрольные вопросы.

1.  Что определяет регулировочная характеристика широтно-импульсного преобразователя?

2.  Почему преобразователи постоянного напряжения в постоянное напряжение называют “электронными трансформаторами постоянного напряжения”?

3.  В чем суть метода осреднения переменных состояния.

4.  Какова процедура метода осреднения переменных состояния.