Синтез управляющих логических устройств на основе карт Карно, страница 2

2.1. Математические основы построения УЛУ

В алгебре логики переменные и функции – логические переменные и логические функции могут принимать только два значения, обозначаемые цифрами 0 и 1. двум указанным значениям ставятся в соответствие различные взаимоисключающие события (действия), условия, состояния в логических устройствах. Например, замыкание контакта – размыкание контакта, наличие сигнала – отсутствие сигнала. Важно отметить, что цифры 0 и 1 и буквенные обозначения переменных в алгебре логики не числа, а символы и алгебра логики – это алгебра состояний.

Входные переменные УЛУ обозначаются обычно буквами латинского алфавита a, b, c, …, промежуточные элементы – буквами p, g. Исполнительные элементы УЛУ и выходные элементы (функции) обозначаются буквами X, Y, Z, F, f.

Различные комбинации значений входных переменных в логических функциях называются наборами. Функция является полностью заданной, если указаны все ее наборы. Для n входных переменных число различных наборов равно 2ⁿ.

В алгебре логики имеется множество операций. Наиболее употребительными из них является полный набор элементарных операций: например, инверсия “НЕ” обозначается черточкой над символом, конъюнкция “ИЛИ” – знаком “+”, дизъюнкция “И” – знаком  “”.  

Логические элементы, которые выполняют основные простейшие логические операции, имеют свои условные обозначения по ГОСТу для составления функциональных схем.

Как любая алгебра, алгебра логики основана на ряде аксиом:

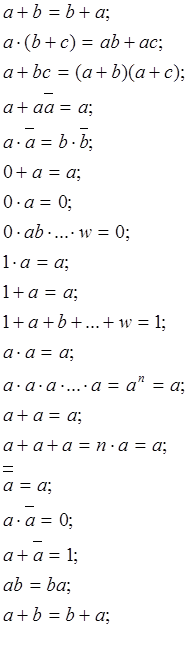
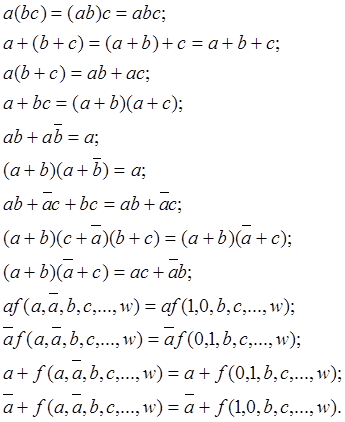
Все эти законы (теоремы) алгебры логики используются как равносильные для преобразования (минимизации) структурных формул УЛУ.

Для облегчения понимания законов алгебры логики и значений функций их представляют в виде релейно-контактных схем.

Используя законы алгебры логики, можно упростить полученное алгебраическое выражение. Такое упрощение необходимо выполнять всякий раз перед реализацией математического выражения “в металле” с использованием логических элементов или программным способом.

2.2. Методы синтеза УЛУ

Существует несколько методов структурного синтеза УЛУ, которые могут быть использованы для циклических систем. Методы эти должны решать задачу синтеза УЛУ в следующей постановке: по словесному описанию порядка и условий функционирования проектируемой системы, т. е. по заданным условиям технологического процесса, получить структурную формулу. Методы отличаются большей или меньшей сложностью освоения, эффективностью применения с точки зрения получения минимизированных алгебраических выражений, преимуществами при использовании для определенных объектов – технологических процессов.

Чаще всего синтез УЛУ выполняют одним из следующих методов: таблиц переходов и карт Карно, алгебры состояния и событий, таблиц включений, циклограмм.

В данном курсовом проекте рассмотрен метод синтеза УЛУ с помощью карт Карно и по заданной таблице включений выполнен синтез управляющего логического устройства системы автоматики методом циклограмм.

3.  Синтез управляющих логических устройств на основе карт Карно

Рассмотрим логическую функцию двух переменных:

Каждому набору данной функции можно поставить в соответствие клетку карты Карно. В эту клетку записывается значение функции для данного набора. Входные переменные располагаются по внешним сторонам карты напротив ее строк и столбцов, при этом значение каждой из входных переменных относится ко всей строке или столбцу и равно единице если напротив строки или столбца стоит под скобкой обозначение этой переменной, для остальных строк (столбцов) значение переменной равно нулю. Количество клеток в карте Карно равно 2ⁿ, где n – число входных переменных.

Карта Карно для рассмотренной выше логической функции двух переменных имеет вид:

0	1
b   a   1	0

Способ заполнения карты Карно по таблице истинности

Для примера возьмем функцию трех переменных: a., b и c. Таблица истинности функции имеет вид:

a	b	c	f
1	1	1	1
1	1	0	1
1	0	1	1
1	0	0	0
0	1	1	0
0	1	0	0
0	0	1	0
0	0	0	0

Карта Карно для данной функции состоит из 8 клеток, в каждой из которых соответствующее состоянию переменных значение функции:

 

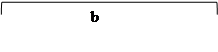0	0	0	0
0	1	1	1

c

Карта Карно также может быть составлена для логической функции, заданной алгебраическим выражением. Для примера составим карту Карно следующей функции: f = .

Необходимо соблюдать следующий порядок действий:

1.  по числу переменных, входящих в выражение, строится карта Карно и располагаются переменные: для нашей функции число переменных n = 3, число клеток карты Карно 2ⁿ=8.

 

a

c

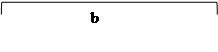2.  заданное алгебраическое выражение приводится к СДНФ:

f = ;

3.  для каждого набора в СДНФ соответствующего единице находится нужная клетка на карте Карно в которую записывается единица. А для набора в СДНФ соответствующего нулю записывается нуль:

 

a   0	1	1	1
0	0	1	0

c

Полученная карта Карно соответствует логической функции f = .

Основные свойства карт Карно

1.  Наборы значений переменных для соседних клеток карты отличаются значением лишь одной переменной. При переходе из одной клетки в соседнюю всегда изменяется значение лишь одной переменной.

2.  Соседними между собой являются крайние левые с крайними правыми и крайние верхние с крайними нижними.