Анализ уравнения Бингама-Шведова. Решение уравнения Букингама для смесей с переменной вязкостью

Анотация

В работе приведены результаты анализа уровнения Бингама-Шведова. Показан метод решения метод решения уравнения Букингама с учетом изменения динамического коэффициента вязкости в функции концентрации твердой фазы. Результат работы дают возможностьразработать методику расчета гидротранспорта высоконцентрированных гидросмесей продуктов переработки минерального сырья.

Введение

Анализ гранулометрического состава продуктов переработки минерального сырья на предприятиях цветной металлургии показывает, что твердое в основном представлено мелкими классами (ЭО.074  - 0.074 мм до –95%). Гидросмеси таких материалов по своим механическим свойствам приближаются к суспензиям, гидромеханические характеристики которых в значительной степени зависят от вязкости. При малой концентрации твердой фазы вязкость гидросмесей мало отличается от  вязкости несущей среды. С увеличением объемного содержания твердой фазы гидросмеси становятся седиментационно-устойчивыми, вязкость смеси резко возрастает, что потверждают результаты вискоизмерительных иследований (1,2). 

1.Анализ уровнения Бингама-Шведова

В основе метематической модели течения концентрированных смесей лежит уровнение Бингама-Шведова, итропретация которого для конкретных случаев течения в итоге привотит к известному уравнению Букингама (3,4). В конечных   уравнениях  вязкость смеси (континуума) представлена как постоянная величина, характерная лишь для ядра потока, а интегрирование приводит к формуле Гагена-Пуазеля. Для кольцевого же слоя этот параметр совсем не учитывается, что всущности приводит к противоречию с исходным уровнением Бингама-Шведова, устанавливающего взаимосвязь динамического коэффицента вязкости и градиента скорости по сечению потока и базирующегося на классических уравнениях Максвела. Поэтому уравнение Букингама для течения концентрировнных мелкофракционных гидросмесей обосновано лишь для малых диаметров труб        (до 50 мм), когда выполнимо соотношение 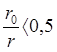 и концентрации гидросмеси (а, следовательно, и вязкость) в ядре мало отличается от концетрации в кольцевом пространстве  (слое). Для промышленных трубопроводов диаметром 150-300 мм. даное уравнение может быть использовано как приближенная модель, адекватность которой должна быть потвержденна эксперементально. В связи с этим  практике пользуются различного вида апроксимоциями уравнения Букингама (5).

2. Решение уравнения Букингама для смесей с переменной вязкостью

Из решения уравнения Бингама-Шведова для двух характерных областей течения в тубопроводе имеем следующее выражение:

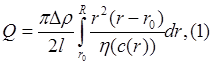
откуда при h=const получим известное решение

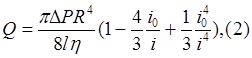
где DR - перепад давления, Па; l – длина участка трубопровода, м; r₀ – радиус ядра потока, м; r – текущий радиус потока, м; R – радиус трубопровода, м; h - динамический коэффицент вязкости, Па*с; С – концетрация твердой фазы; i₀, i – гидравлический уклон в ядре потока и в области потока с радиусом r.

 Если ввести координату 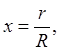то граничные условия для (1) можно записать в видде:    r = R; x = 1; r₀ = r;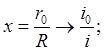

тогда общий расход (т.е. сумма расходов в ядре потока и в кольцевом слое) будет равен:

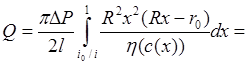
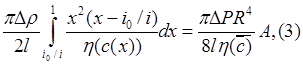
где .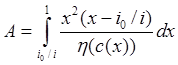

В формуле (3) вязкость зависит от величины концентрации, которая изменяется по сечению потока, уменьшаясь от среднего значения в ядре () до 0 на границе потока с радиусом R. Для упращения решения используем линейную зависимость уменьшения концентрации в направлении от ядра потока, т.е.

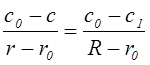  и

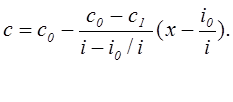
Если заменить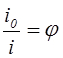, то для А из формулы (3) можно записать интеграл:

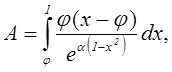
решение которого приводит к виду:

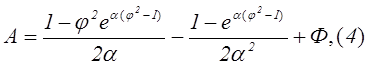
где

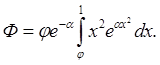
Остановливаясь на данном решении, отметим, что коэффициент a для большого класса гилросмесей хвостов обогащения полиметалических руд близок к 1, тогда итеграл А принемает вид:

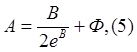
где

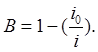
В итоге, для суммарного расхода концентрированной гидросмеси в соответствии с формулой (3) окончательно будем иметь выражение:

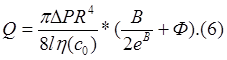
В рамках даннай работы не предстовляется возможным дать глубокий анализ формулы (6). Однако, при наличии эксперементальных данных по вискозиметрии в виде  открывается возможность построения методики расчета гидротранспорта высококонцентрированных смесейпродыктов перерабтки минерального сырья.

Заключение

Выполненная исследовательская работа позволяет поновому подойти к расчету режимов гидравлического транспорта высококонцентрированных мелкофракционных гидросмесей. В предложенной математической модели учитевается все основные параметры, характеризующие реологические свойства жидкой вязкопластичной системы. В работе показано, что динамический коэффициент вязкости гидросмеси является функцией объемной концентрации твердой фазы и от правельного выбора закона изменения концентрации по сечению потока зависит успешное решение практической задачи расчета гидравлических сопротивлений при гидравлическом транспорте концентрированных смесей. 

Литература

1.  Александров В.И. Влияние вязкости жидкости на прочность закладки. (Прикладные аспекты гидротранспортирования продуктов обогащения минерального сырья. Междуведомств. сб. научн.  тр. ) ‘Механобр’, Л.,1987 г., с.116-119.

2.  Джунусов И.Ш. Реологические свойства текущих хвостов Джезкказганского ГМК. (Прикладные аспекты гидротренспортирования продуктов обогащения минерального сырья. Междувед.сб. научн. тр.), ‘Механобр’, Л.,1987 г., с.110-116.

3.   Смолдырев А.Е., Сафанов Ю.К., Трубопроводный транспорт концентрированных гидросмесей. М., ‘Машиностроение’, 1973 г., с. 208.

4.  Ребиндер А.Е. Физико-химическая механика. М., 1958.

5.  Латыпов Э.К., Филатов Б.С. Об аппроксимациях уравнения Букингама для вязкопластичного течения дисперстных систем. Коллоидный журнал. Т. 25, 1963 г., № 1.