Построение формы напряжения на выходе. Одиночные прямоугольные импульсы

Тогда амплитудно-частотная и фазово-частотная характеристики примут вид:

.

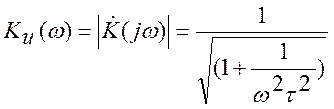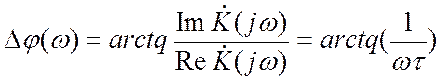
Графики амплитудно-частотной и фазово-частотной характеристик для заданной дифференцирующей цепи приведем на рис. 4 и рис. 5 соответственно.

Ширина полосы пропускания дифференцирующей CR – цепи равна частоте среза

w_ср=1/t=1/10^-7=10⁷ (рад/с)

f_ср=w_ср/2p=15,92×10⁶ Гц

wср

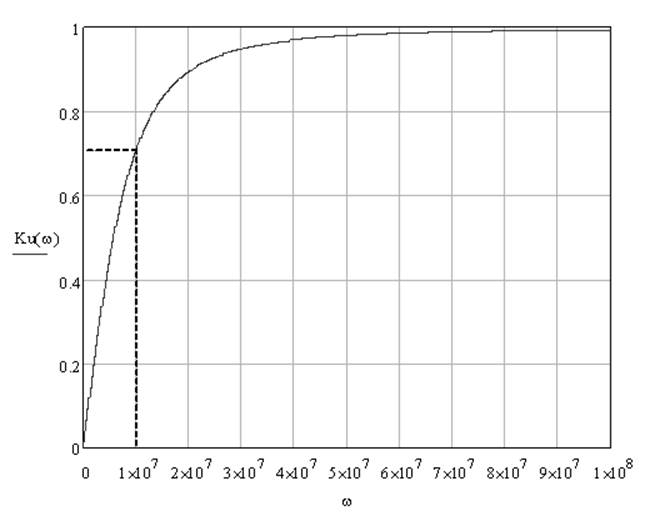
Рис. 4

wср

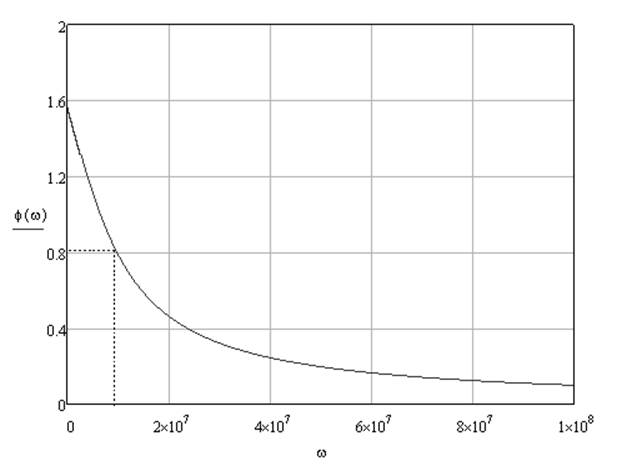
Рис. 5

Пусть на вход этой же дифференцирующей (рис. 1) цепи воздействуют периодические прямоугольные импульсы с частотой 100 кГц, длительностью t_и = 1 мкс.

Определим отклик дифференцирующей цепи на данное воздействие спектральным методом. Для этого произведем разложение периодической последовательности импульсов в ряд Фурье в вещественной форме. Ограничим количество гармонических сигналов в ряде равным 100, что позволит получить сигнал с довольно высокой точностью.

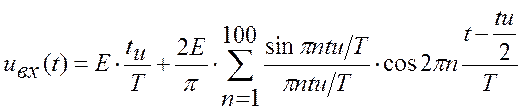
Амплитудно-частотная и фазо-частотная характеристики цепи имеют вид:

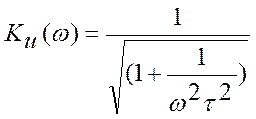
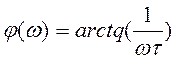
Отклик на выходе цепи будет представлять собой произведение каждой гармоники входного сигнала на частотный коэффициент передачи цепи на соответствующей частоте, с учетом того что коэффициент передачи постоянной составляющей равен нулю имеем:

 

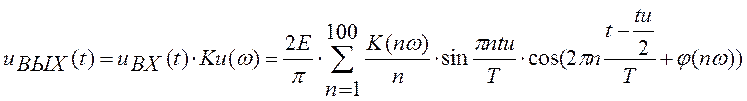
С учетом равенств:

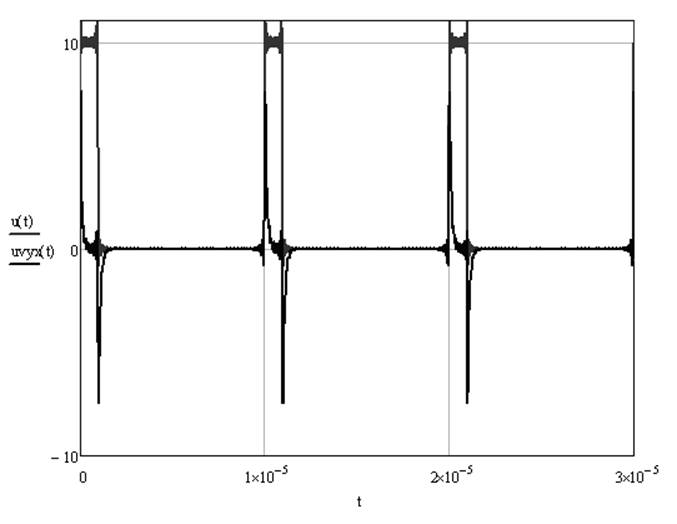
Построим временные диаграммы u_вх(t) и u_вых(t) при помощи пакета MathCAD.

Задание №2 (методическое пособие № 1 , КР № 1 задание 5)

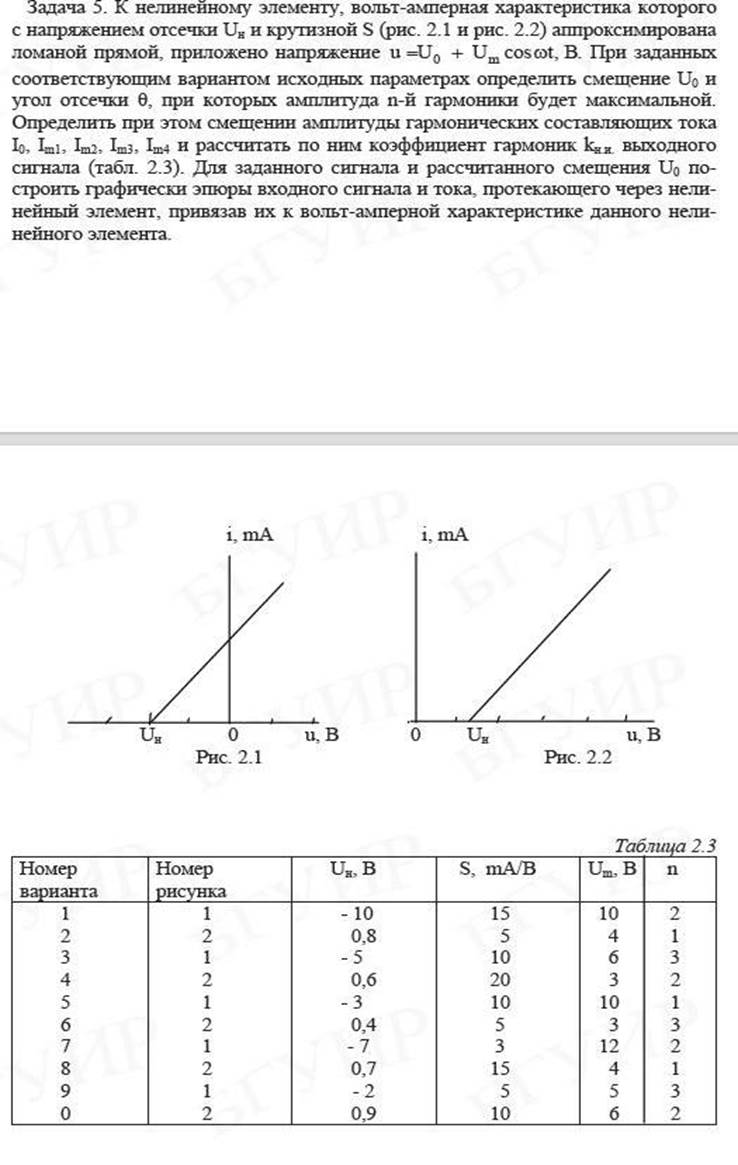
Решение

Большое применение находит аналитический метод анализа, получивший название метода угла отсечки. Угол отсечки, численно равен половине той части периода, в течение которого через НЭ протекает ток.

Угол отсечки легко найти из равенства :

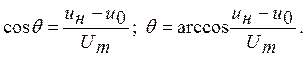    (1)

Угол отсечки, соответствующий максимуму n-ой гармоники в спектре тока (при ) определяется по формуле:

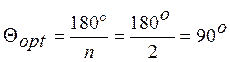
Выразив в формуле (1) u₀ получаем смещение при котором на выходе НЭ вторая гармоника тока будет максимальной.

Функция тока определяется следующим выражением:

. (2)

При :

 

Амплитуды спектральных составляющих тока через НЭ определяются через коэффициенты Берга:

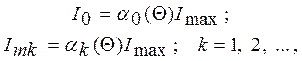     (3)

где коэффициенты  являются функциями одного аргумента – угла отсечки , получили название коэффициентов (функций) Берга.

Функции Берга можно определить по следующим формулам

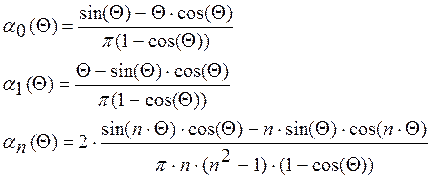
Значения функций Берга для угла отсечки равного 90⁰ сведем в таблицу 1.

Таблица 1

a0	a1	a2	a3	a4
0,318	0,5	0,212	0	-0,042

Согласно формуле (3) спектральные составляющие тока равны:

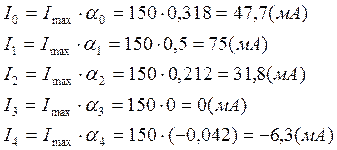
Коэффициент гармоник определим по формуле:

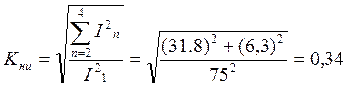
Эпюры входного сигнала и тока протекающего через НЭ приведем на рис.1.

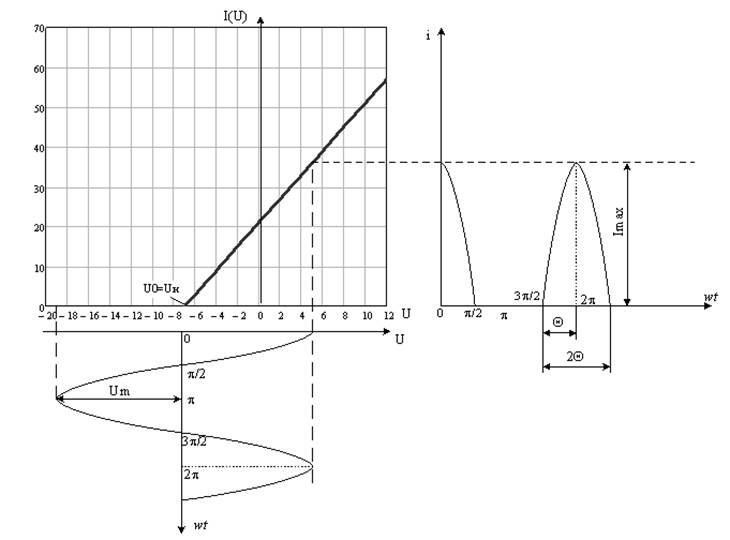
Рис. 1

Задание №3 (методическое пособие № 1 , КР № 2 задание 1)

(для таблицы 2.4 вариант №1)

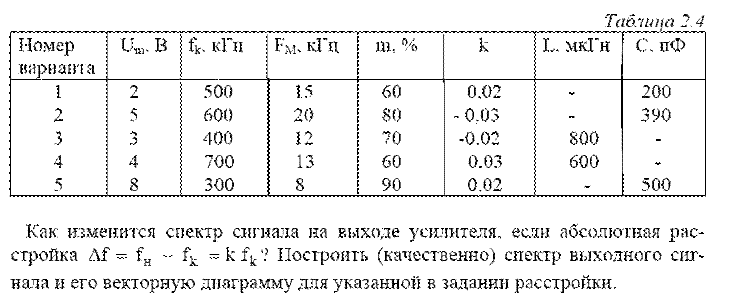
Решение:

Представим произведение косинусов их суммой и подставим данные для варианта 2

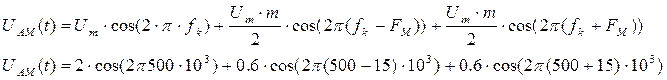
Как видно из выше приведенной формулы,  в спектре однотонального AM-сигнала будут присутствовать колебания на трех частотах, а именно: f_k – несущая частота; (f_k-F_M) – нижняя боковая частота и (f_k+F_M) – верхняя боковая частота. Спектр АМ-сигнала приведен на рис. 1.

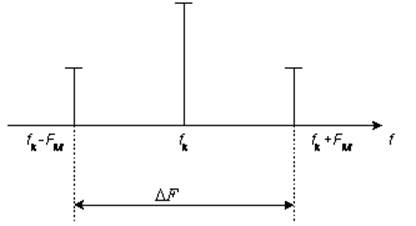
Рис. 1

Как видно из рисунка 1 ширина спектра АМ-сигнала будет равна:

Для того чтобы АМ-сигнал не искажался контуром резонансного усилителя необходимо чтобы полоса пропускания контура была не менее полосы АМ-сигнала. В связи с этим определим добротность колебательного контура:

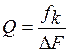          где f_k – резонансная частота контура равная 500 кГц;

 - полоса пропускания контура равная 30 кГц

Тогда добротность контура равна:

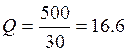
Выразим индуктивность контура из формулы:

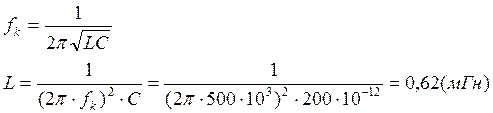
Выразим добротность контура через характеристическое сопротивление контура r и сопротивление потерь в контуре R:

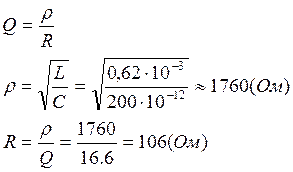
Определим частоту расстройки резонансного контура при k= 0,02

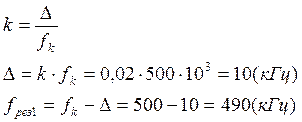
Качественно спектр АМ-сигнала с контуром настроенным на несущую