Связь термокинетических параметров разрушения
горных пород со структурными и молекулярными данными среды.
При взрывном разрушении возникают быстропеременные нагрузки двух типов - волновые и квазистатические. При действии волн напряжений на некоторый выделенный объем нагрузка носит динамический характер до достижения максимальных значений напряжений, после чего происходит статическая разгрузка до нормальных напряжений. Вследствие разности кривых нагрузки и разгрузки в частицах остаётся часть энергии.
Эта диссипированная энергия не участвует в дальнейшем формировании механических возмущений, что приводит к снижению параметров волн напряжений по сравнению со взрывом в идеально - упругой среде. С другой стороны запасённая в частицах энергия расходуется вначале на повышение температуры среды и по мере остывания - к возникновению трещин и увеличению их размеров.
Есть несколько методов расчёта образования, накопления количества и увеличения размеров трещин:
- идеальная прочность, основанная на расчёте энергии разрыва межмолекулярных связей в бездефектной среде;
- теория Гриффитса, основанная на оценке возможности увеличения размеров существующих трещин за счёт превышения упругой энергии над поверхностной;
- кинетическая теория прочности, позволяющая оценить скорость накопления микротрещин определенных размеров и соответственно их количество за время динамической нагрузки. Следует также отметить теорию прочности Кулона-Навье, позволяющую учитывать влияние нормального напряжения при образовании трещин сдвига.
Все отмеченные подходы к процессам разрушения можно объединить и найти необходимые параметры разрушения в развиваемой термокинетической теории разрушения.
При образовании поверхностного слоя трещины происходит фазовый переход
1-го рода, когда скачком изменяются формы движения молекул. В работах Надаи, ФТИ РАН и других установлено, что частоты колебаний поверхностных молекул существенно ниже, а амплитуды выше, чем молекул, расположенных в монолитном объёме. Таким образом, если определить термодинамические функции молекул, расположенных в монолитном объёме и на поверхности трещин, то можно найти условие фазового перехода.
Имеется три направления нормальных колебаний:
перпендикулярно поверхности трещины и в двух взаимно перпендикулярных направлениях в плоскости поверхности. При образовании трещины отрыва происходит разрыв межмолекулярных связей и поэтому изменение частоты и амплитуды колебаний происходит только в направлении по нормали к поверхности. Две другие составляющие колебаний остаются без изменений. Раскрытие трещины представляет собой переход состояния среды от монолитного к поверхностному вдоль поверхности трещины.
В работах [1,2] рассмотрен фазовый переход первого рода в горных породах, происходящий в поверхностном слое молекул при образовании микротрещины. В этом слое изменяются энергия электронного возбуждения молекул, энергия взаимодействия между молекулами, затрачивается энергия на разрыв межмолекулярных связей. Все эти изменения описываются выражениями для статистических сумм и свободных энергий.
Условием фазового перехода является минимум свободной энергии Fs ансамблей частиц, расположенных на сомкнутых и раскрытых частях потенциальных и реальных поверхностей трещин.
Свободная энергия Fs может быть определена в виде:
![]()
где ![]() ,
,![]() количество частиц, расположенных на
сомкнутых и раскрытых поверхностях трещин соответственно;
количество частиц, расположенных на
сомкнутых и раскрытых поверхностях трещин соответственно;
![]() ,
,![]() -статистические
суммы
-статистические
суммы
![]() - постоянная Больцмана
- постоянная Больцмана
Статистическая сумма для канонического распределения Гиббса определяется выражением:
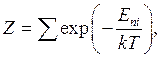 (2)
(2)
где
![]() - энергия n-го квантового
состояния системы.
- энергия n-го квантового
состояния системы.
В
твердом теле между молекулами существует сложное взаимодействие, приводящее к
вполне определённым энергетическим состояниям и формам движения. Из этих
состояний основными являются колебательные движения молекул относительно узлов
кристаллической решетки, упругое взаимодействие между молекулами и электронное
состояние. Поэтому ![]() можно представить как:
можно представить как:
![]() =
=![]() +
+![]() +
+![]()
где ![]() ,
,
![]() ,
, ![]() -
энергии колебательного движения, упругого взаимодействия и электронного
состояния.
-
энергии колебательного движения, упругого взаимодействия и электронного
состояния.
Все эти три компоненты энергии претерпевают изменения при переходе из монолитного состояния в приповерхностное.
Введем концентрацию молекул, находящихся в поверхностном слое:
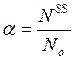
где
![]() =
=![]() +
+![]() . Тогда свободная энергия всего
ансамбля
. Тогда свободная энергия всего
ансамбля ![]() частиц определяется выражением:
частиц определяется выражением:
![]() (3)
(3)
где 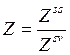 -
параметр фазового перехода. /.
-
параметр фазового перехода. /.
Величина
![]() находится из выражения для минимума
свободной энергии при вариации
находится из выражения для минимума
свободной энергии при вариации ![]() .
.
Статистическая сумма колебательных движений имеет вид:
![]() (5)
(5)
где
h - постоянная Планка; ![]() - максимальная
частота колебаний молекул.
- максимальная
частота колебаний молекул.
В
приближении Дебая величина ![]() определяется
соотношением:
определяется
соотношением:
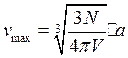
где а — скорость звука в среде.
При
![]()
![]() выражение
(5) принимает вид:
выражение
(5) принимает вид: ![]() =
=![]() /kT
/kT
Из (2) и (3) с учетом принятых обозначений следует:
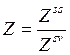 =
=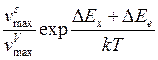
или,
так как ![]() , где
, где ![]() -
период колебаний,
-
период колебаний,
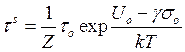 (8)
(8)
где ![]() =
=![]() -
разность основных уровней электронного состояния.
-
разность основных уровней электронного состояния.
В области
разрушения ![]() и Z
и Z![]() 1
1
Из
формулы (8) при условии ![]() следует:
следует:
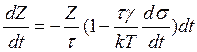 (11)
(11)
В
кинетической теории прочности долговечность разрушения ![]() определяется
формулой С.Н. Журкова.
определяется
формулой С.Н. Журкова.
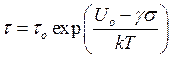 (9)
(9)
где
![]() - энергия активации разрушения,
- энергия активации разрушения, ![]() - структурный коэффициент
- структурный коэффициент
![]() - период колебаний молекул в монолитной среде.
- период колебаний молекул в монолитной среде.
Из сравнения (9)
и (10) следует, что долговечность разрушения ![]() связанна
с частотой колебаний поверхностных молекул
связанна
с частотой колебаний поверхностных молекул ![]() и
параметром фазового перехода z определяется
минимумом свободной энергии.
и
параметром фазового перехода z определяется
минимумом свободной энергии.
При
разрушении происходит образование двух типов трещин -сдвига и отрыва. В каждом
из этих случаев происходят различные свои перестройки электронных уровней.
Меньшие перестройки происходят при образовании трещин сдвига, наибольшие -
трещин отрыва. При образовании трещин отрыва изменение энергии основного
электронного состояния равно энергии сублимации. При образовании трещин сдвига ![]() .
.
Для трещин сдвига и отрыва измерения Uо в горных породах выполнены А.Н.Ставрогиным и Б.Г.Тарасовым [3]. В работе [3] показано, что при образовании трещин сдвига Uo близко энергии самодиффузии Есд, а для трещины отрыва Uo близко энергии сублимации. К аналогичным результатам пришли авторы работ [4,5].
Самодиффузия представляет собой изменение формы и размеров тела, обусловленное диффузионными перемещениями частиц. В качестве 1-го приближения принимается
![]() Eсд=0,032Тпл (10)
Eсд=0,032Тпл (10)
где Тпл - температура плавления.
При
образовании трещин отрыва происходит полный разрыв связей между элементарными
частицами и более глубокая перестройка электронных состояний. При сдвиге
полного разрыва связей не происходит. Из экспериментов, выполненных Ставрогиным
А.Н. с сотрудниками в [3] установлено, что энергия активации при образовании
трещин отрыва примерно в 2 раза выше, чем при сдвиге и при кручении. Величина
![]() представляет собой изменение
упругой энергии
представляет собой изменение
упругой энергии
взаимодействия молекул при образовании поверхностного слоя трещины. Очевидно, что такое изменение энергии различно для трещин отрыва, трещин сдвига только под действием сдвигового напряжениями трещин сдвига при наличии нормальных к поверхностям трещин напряжений. Последний случай соответствует сжимающим напряжениям.
Простейший случай соответствует простому сдвигу. В этом случае для обеспечения сдвига достаточно просто нарушить кристаллическое строение среды. Физически это можно представить себе как изменение удельного объёма при плавлении, то есть изменение упругой энергии взаимодействия можно представить себе как
![]() (11)
(11)
где
![]() - максимальное напряжение в вершине трещины,
связанное с напряжением в среде
- максимальное напряжение в вершине трещины,
связанное с напряжением в среде ![]() условием
условием

![]() - длина
трещины,
- длина
трещины,
![]() -
постоанная кристаллической решётки.
-
постоанная кристаллической решётки.
Из (11),(12) следует:
![]()
где
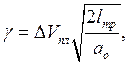 - структурный коэффициент .
- структурный коэффициент .
Формулу (13) представим в виде:
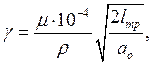
учитывая,
что 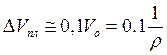 ;
; ![]() -
молекулярный вес.
-
молекулярный вес.
При наличии сжимающих напряжений, действующих одновременно со сдвиговыми, они препятствуют плавлению.
Тогда принимая формулу Кулона-Навье для совместного действия сдвиговых и сжимающих напряжений, получим:
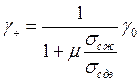 ,
,
В процессе образования трещины отрыва затрачивается работа, которую можно приближённо оценить, используя подход Орована и Полани при получении зависимости для идеальной прочности.
Атомная связь на единицу площади обычно аппроксимируется зависимостью
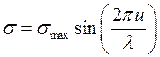 ,
,
где
![]() - длина волны, u -
смещение от положения равновесия в кристаллической решетке. При u=
- длина волны, u -
смещение от положения равновесия в кристаллической решетке. При u=![]() /4
/4 ![]() =
=![]()
Тогда
энергия на единицу поверхности, затрачиваемая на берегов трещины размером ![]() .
.

![]()
где Е - модуль упругости;
![]() - максимальная деформация;
- максимальная деформация; ![]() -
идеальная прочность
-
идеальная прочность
Энергия затрачиваемая на разрыв двух атомов или молекул
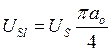 ,
,
а на разрыв NAV молекул
U = NAV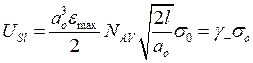
где
![]() - структурный коэффициент формулы
С.Н.Журкова для долговечности при растягивающих напряжениях.
- структурный коэффициент формулы
С.Н.Журкова для долговечности при растягивающих напряжениях.
Для
кварца ![]() м
м
Тогда
![]() м/моль
м/моль
Таким образом получены соотношения для термокинетических параметров среды, определяемых с помощью молекулярных и структурных данных среды.
1. Энергия активации разрушения для трещин сдвига
![]()
где
![]() - температура плавления
- температура плавления
2. Энергия активации для трещин отрыва /
![]()
3. Структурный коэффициент, формулы для долговечности разрушения
- для трещин сдвига:
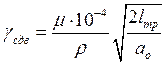 ,м3/моль
,м3/моль
где ![]() - плотность среды, кг/м3
- плотность среды, кг/м3
- для трещин сдвига при наличии сжимающих напряжений:
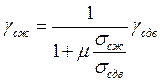
- для трещин растяжения
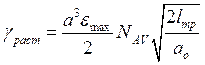
где 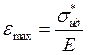 - предельная деформация
- предельная деформация
![]() -
модуль упругости
-
модуль упругости
![]() -
постоянная кристаллической решетки
-
постоянная кристаллической решетки
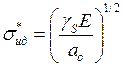 -
идеальная прочность
-
идеальная прочность
![]() -
поверхностная энергия
-
поверхностная энергия
Поверхностная энергия связана с энергией активации разрушения соотношением
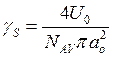
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.