Природа и характер химического равновесия. Изотерма и изобара химической реакции. Принцип подвижного равновесия, страница 2

С термодинамической точки зрения химические реакции необратимы, поскольку до наступления равновесия они протекают с конечными скоростями. Тем не менее, можно мысленно представить, что эти реакции в обоих направлениях протекают бесконечно  медленно, через равновесные состояния. Это означает, что при постоянстве концентраций и неизменных внешних условиях они термодинамически обратимы, а  равновесная реакционная система должна характеризоваться общими условиями термодинамического равновесия.  Эти условия для конкретной ситуации представлены в таблице 1.6. Например, если равновесная реакционная система находится при постоянных давлении и температуре, то условием равновесия для этой системы будет равенство нулю изменения энергии Гиббса, т.е. DG = 0.

Гетерогенную систему удобно  характеризовать термодинамическими условиями равновесия, выраженными с помощью представлений о химическом потенциале, т.е.:

åm_idn_i = 0                                                     (4.8)

Таким образом,  химическое равновесие обладает кинетическими и термодинамическими характеристиками.

4.2. ИЗОТЕРМА ХИМИЧЕСКОЙ РЕАКЦИИ

Особенно выразительно  двойственная природа химического равновесия проявляется при рассмотрении вывода изотермы химической реакции.

Рассмотрим уравнение химической  реакции, записанное в общем виде (см. выражение 4.1). 

Предположим, что реакция протекает в газовой фазе при постоянных температуре и давлении. Пусть реагенты имеют свойства идеального газа. В этом случае изменение энергии Гиббса можно выразить уравнением:

DG = b₁m₁ + b₂m₂+. . . .-(a₁m₁ + a₂m₂ +. . . )                        (4.9)

С учетом того, что для идеального газа m_i(T) = m_i⁰(Т) + RTlnp_i (1.64).    можно записать, что                                        

DG = å[b_im_i⁰(Т) ] + RTå[b_i lnp(B_i)]  -å[(a_im_i⁰(Т) -RTå[a_ilnp(B_i)]    (4.10)

Обозначим:

å[b_im_i⁰(Т) ] -å[(a_im_i⁰(Т)] = DG ^о                                                        (4.11)

где  DG^о - постоянная для данной температуры величина, а также:

 и                                        (4.12)

С учетом введенных обозначений уравнение  (4.10) примет вид:

                                    (4.13)

Для равновесных условий DG = 0, поэтому

, а также 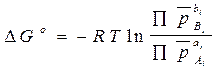                    (4.14)

Поскольку DG ^о  и RT  постоянны, то и отношение 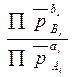 есть величина постоянная,  соответствующая, как видно из уравнения (4.5) константе равновесия  реакции (4.1),  т.е.: 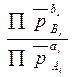   = К_р.  С учетом этого соотношения и (4.14) нетрудно  найти связь между изменением энергии Гиббса  и величиной К_р, которая имеет вид:

DG^o = - RTln К_р,                                            (4.15)

Сопоставляя уравнения (4.13) и (4.14) можно получить выражение:

                             (4.16)

С  учетом (4.15) имеем:

                             (4.17)

Последнее уравнение называется уравнением изотермы химической реакции. Его часто  используют для оценки направленности реакции при различных исходных составах  реакционной смеси. Для этого сравнивают значения К_р  и 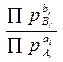  . Если константа равновесия превышает отношение заданных парциальных давлений (или концентраций), то DG < 0  и, как видно из таблицы 1.6,  реакция пойдет в прямом направлении. Если наоборот, тогда DG >0 и следует ожидать, что реакция пойдет в противоположном направлении.

Величина константы равновесия зависит от способа выражения концентраций веществ, образующих равновесную систему. Поэтому используя уравнение состояния идеального газа p = сRT нетрудно перейти к выражению изотермы химической реакции с концентрационной константой равновесия, а с учетом связи между активностью вещества и его аналитической концентрацией – к записи изотермы с термодинамической  константой равновесия.

4.3.  ИЗОБАРА ХИМИЧЕСКОЙ РЕАКЦИИ

(зависимость константы равновесия от температуры)

С изменением температуры положение равновесия химической реакции смещается. Поэтому константа равновесия является функцией температуры.

Рассмотрим уравнение изотермы химической  реакции (4.17). Отношение 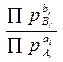 содержит  произвольно задаваемые давления и поэтому от температуры не зависит. Учитывая это, продифференцируем уравнение изотермы по температуре и получим:

                 (4.18)

Подставим в  уравнение Гиббса - Гельмгольца  (4.19),  см. также (1.65):

(4.19) выражения для DG и  ,  представленные уравнениями  изотермы (4.17) и (4.18) соответственно.  После некоторых преобразований полученного уравнения приходим к дифференциальной форме уравнения изобары химической реакции (изобара Вант –Гоффа):

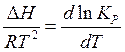                                             (4.20)