Методы учета ограничений в задачах нелинейного программирования

Лабораторная работа №3

Содержание:

• Общие сведения
• Учет ограничений в форме равенств
• Метод прямой оптимизации
• Метод приведенного градиента
• Метод множителей Лагранжа
• Учет ограничений в форме неравенств
• Теорема Куна-Такера
• Метод штрафных функций
• Программное обеспечение
• Порядок выполнения работы
• Контрольные вопросы

МЕТОДЫ УЧЕТА ОГРАНИЧЕНИЙ В ЗАДАЧАХ НЕЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ

Цель работы: изучение и исследование методов учета ограничений в форме равенств и неравенств в задачах нелинейного программирования.

Общие сведения

Рассмотрим задачу нелинейного программирования:

где X = (X₁,X₂,...,X_n) - вектор неизвестных, G(Х)={g₁(X),g₂(X),...,g_m(X)}-вектор-функция ограничений.

Подобные математические модели применяются довольно часто.

Рассмотрим лишь два примера из области энергетики.

1. Оптимизация распределения нагрузки между ТЭС.

Критерием является минимум расхода топлива на всех n ТЭС системы. В качестве неизвестных принимаются мощности Р_i ТЭС, образующие вектор Р. Ограничения определяются балансом мощностей в системе без учета или с учетом потерь в сети и рабочим диапазоном мощностей при заданном составе работающего оборудования ТЭС.

Математическая модель имеет вид:

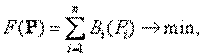
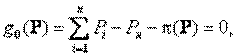
В_i(P_i)– расходные характеристики ТЭС, (P)– функция потерь в сети, P_н – суммарная нагрузка системы, P_imax– предельно-допустимая мощность i-ой ТЭС.

2. Выбор схемы развития сети.

Критерием выбора является минимум затрат на сооружение ЛЭП. Вектор неизвестных P включает потоки P_s по ветвям расчетного графа сети, имеющего избыточные ветви. Вектор-функция ограничений учитывает балансы в узлах сети.

Математическая модель:

где – функция затрат в ветвь s,M– матрица инциденций узлы-ветви, Р_вн – вектор узловых мощностей.

вернуться к началу

1. Учет ограничений в форме равенств.

Рассматривается задача нелинейной оптимизации:

где X=(X₁,X₂,...,X_n) - вектор неизвестных, G(Х)={g₁(X),g₂(X),...,g_m(X)}– вектор-функция ограничений типа g_i(X)=0.

вернуться к началу

1.1. Метод прямой оптимизации.

В этом методе вектор-функцию G(X)=0 рассматривают как систему из m уравнений для n неизвестных при m<n. Такая система уравнений имеет множество решений, найти которое можно выразив m неизвестных из вектора X через остальные k=n-m переменных.

Первые m переменных назовем зависимыми и обозначим через Y, за вторыми k-независимыми сохраним обозначение Х.

Функциональный вид Y(Х) определяется системой G(X)=0. С учетом зависимости Y(Х) и целевую функцию можно преобразовать к новому виду

и найти любым методом безусловной оптимизации такие значения независимых Х=(x₁,x₂,..,x_k), которые отвечают минимуму F(Х). По найденным Х определяются и остальные переменные Y(Х).

Рассмотрим пример оптимизации режима работы 3-x ТЭС на общую нагрузку, равную 100 МВт. Расходные характеристики ТЭС заданы аналитически в виде:

Математическая модель:

Таким образом, имеем систему ограничений, для которой m =1, n =3, k=n-m=2. В качестве независимых примем Р₁ и Р₂. Тогда зависимые Р₃=100–Р–Р₂; и

Решая градиентным методом, получаем Р₁=23 МВт, Р₂=31 МВт. Зависимая переменная Р₃=100–Р₁–Р₂=46 МВт. Оптимальный расход топлива составляет 67.0 тут.

вернуться к началу

1.2. Метод приведенного градиента.

Метод прямой оптимизации применим, когда удается решением системы G(X)=G(Y,Х)=0 найти аналитическую зависимость Y(Х). Однако часто вектор-функция G(X) нелинейна и решение можно получить только численными методами.

Рассмотрим такой случай:

F(Y,Х) = min, G(Y,Х) = 0 , где Y,Х –подмножества зависимых и независимых переменных исходного вектора X.

При бесконечно малых приращениях составляющих векторов Х и Y имеем:

Кроме того для вектор-функции запишем

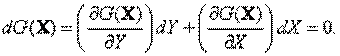
Здесь все производные берутся с учетом явной зависимости от Y и Х.

Решим последнее уравнение относительно dY и, подставив в приращение функции dF, получим:

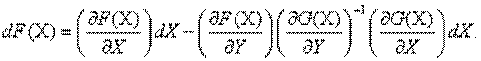
Отсюда получим выражение для градиента по независимым переменным, который называют приведенным,

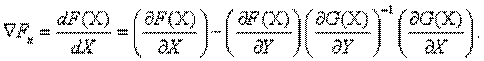
Он может использоваться в алгоритме градиентного метода

Приведенный градиент является проекцией градиента на поверхность ограничений. В точке решения задачи он должен быть равен нулю.

вернуться к началу

Метод множителей Лагранжа

Рассмотрим вновь задачу

Решение ее лежит в точке, где приведенный градиент равен нулю

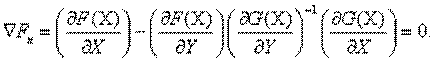
Обозначим часть вычитаемого через U

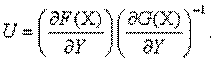
С учетом этого предыдущее условие можно записать в виде эквивалентной системы уравнений:

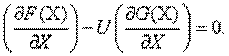
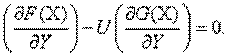
Полученная система соответствует условию минимума некоторой функции, называемой функцией Лагранжа,

где U – вектор множителей Лагранжа.

Оказывается, функцию Лагранжа можно составить для исходной задачи без разделения вектора X на зависимые Y и независимые Х подмножества:

Таким образом, решение исходной задачи определяется выполнением условия минимума функции Лагранжа.

Сформированная система из n+m уравнений позволяет найти все n+m неизвестных, включая и неопределенные множители Лагранжа.

В практических задачах оптимизации метод имеет ограниченное применение. Однако он широко используется при теоретическом анализе и в инженерных методах оптимизации в энергетике.

Рассмотрим ,например, задачу распределения нагрузки между ТЭС в системе, математическая модель которой была ранее составлена:

Запишем функцию Лагранжа

и условия минимума ее:

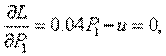
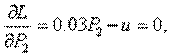
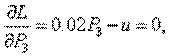
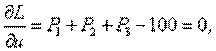
Решение этой системы: u=0.92, Р₁=23, Р₂=31, Р₃=46.