Методы учета ограничений в задачах нелинейного программирования, страница 2

вернуться к началу

2. Учет ограничений в форме неравенств.

Общую задачу нелинейного программирования запишем следующим образом:

где X=(X₁,X₂,...,X_n) – вектор неизвестных, G(Х)={g₁(X), g₂(X),...,g_m(X)}, H(X)={h₁(X),X),…,h_k(X)} – вектор-функции ограничений.

Наибольшие трудности возникают при учете ограничений H(X) в форме неравенств. Простой и очевидный на первый взгляд метод, заключающийся в поиске решения без учета ограничений, последующей проверке их выполнения и закреплении переменных, вышедших за допустимые пределы, на границе, часто дает ложные результаты.

Пример подобной ситуации приведен на рис 3.1. Здесь безусловный минимум лежит в точке X=(4,4). Проверка ограничений показывает, что h₁(X), h₂(X) нарушены. Граничные значения х₁=3.8 и х₂=2.8 определяют ложное решение. Фактическое решение лежит в точке X=(3.05,2.8), где ограничения h₁(X), h₃(X) выполняются в форме неравенств и называются пассивными, а ограничение h₂(X) в этой точке является активным.

В проблеме учета ограничений в форме неравенств важную роль играет теорема Куна-Такера (теорема о седловой точке).

вернуться к началу

2.1. Теорема Kуна-Такера.

Пусть дана задача

(3-1)

Составим функцию Лагранжа для этой задачи.

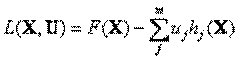
Если допустимое множество X, определяемое вектор-функцией H(X)>=0, не пустое, то имеет место следующая теорема:

Вектор X_o тогда и только тогда является решением задачи (1), когда существует такой вектор U_o, что при X_o>=0 и U_o>=0 для всех X>=0 и U>= 0 справедливо

(3-2)

Точка (X_o,U_o) называется седловой точкой, т.к. здесь обеспечивается минимум по X и максимум по U.

Если функции F(X), h_j(X) дифференцируемы, то (3-2) можно заменить условиями Kуна-Такера для всех <>X_io>=0 и U_jo>= 0

;

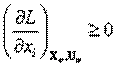
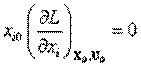и .

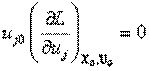вернуться к началу

2.2. Метод штрафных функций.

Идея метода заключается в том, что задача с ограничениями заменяется задачей безусловной оптимизации некоторой обобщенной целевой функции, в которую введены "штрафы" за нарушение ограничений.

Пусть имеется исходная задача

Новая целевая функция имеет вид:

где S_j, S_i – коэффициенты, определяющие жесткость ограничений; d_i - коэффициент, равный 1, если h_i(X)< 0, и 0 в остальных случаях.

В допустимой области штрафы, определяемые функциями h_i(X) и >g_j(X), отсутствуют. За пределами ее они резко возрастают, увеличивая Р(X), что делает выход за границу невыгодным.

Преимущество и эффективность метода заключаются в том, что минимизация Р(X) может проводиться более простыми методами безусловной оптимизации.

Важную роль в методе штрафных функций играют коэффициенты жесткости ограничений. С ростом S возрастает точность выполнения ограничений, но ухудшается сходимость, т.к. Р(X) вблизи границы приобретает характер "овражной" функции.

Сочетание штрафных функций и методов нулевого порядка позволяет создавать эффективные алгоритмы и программы для решения общей задачи нелинейного программирования. Ниже приведены примеры траекторий решения следующей задачи:

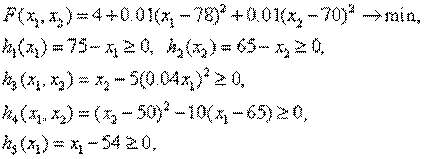
методом случайного поиска (рис 3.3).

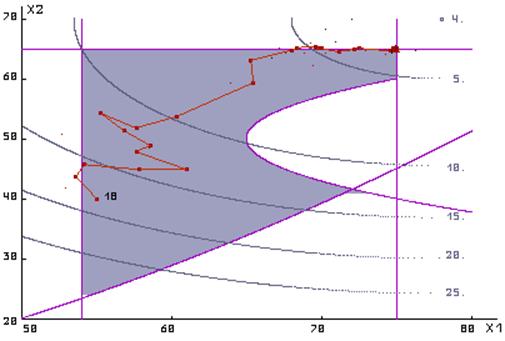
Рис.3.3

вернуться к началу

Программное обеспечение

Основы нелинейного программирования и методы учета ограничений в примерах и иллюстрациях представлены в программе ACYLB3.exe в объеме, необходимом для самостоятельного изучения проблемы.

вернуться к началу

Порядок выполнения работы

1. Запустить  Start.bat и ознакомиться с особенностями и методами учета ограничений в задачах нелинейного программирования.
2. Найти методом прямой оптимизации оптимальную нагрузку без учета потерь в сети 3-х ТЭС с расходными характеристиками: при заданной общей нагрузке Р_о (Табл.3.1).
3. При той же нагрузке найти методом приведенного градиента оптимальную мощность 2-х ТЭС, расходные характеристики которых 
4. Решить задачу 2 методом множителей Лагранжа.
5. Оценить влияние Sна жесткость выполнения ограничений в методе штрафных функций.
6. Построить траектории решения рассмотренной в 2.2 задачи методами нулевого порядка с учетом ограничений по методу штрафных функций при заданных Хо и dX.
7. Все этапы исследований отразить в отчете.

Таблица 3.1.

№	P0	X0	dX
1	200	55,22	10
2	190	60,35	10
3	180	55,40	6
4	170	60,66	6
5	160	65,25	4
6	150	66,50	4
7	140	63,28	8
8	130	50,45	8

вернуться к началу

Контрольные вопросы

1. Привести примеры математических моделей, в которых учитываются ограничения.
2. Какой вид имеет допустимая область при разных типах ограничений?
3. Как учитываются ограничения-равенства в методе прямой оптимизации?
4. Как учитываются ограничения-равенства в методе прямой оптимизации?
5. Как меняется длина приведенного градиента по мере приближения к решению?
6. Чем определяется количество множителей Лагранжа?
7. Почему при использовании штрафных функций решение лежит за границей допустимой области?
8. Как должен выбираться шаг в методах скорейшего поиска с учетом ограничений?

вернуться к началу