Примеры оптимизационных моделей для обсуждения. Изучение способов построения оптимизационных моделей

каждой задаче прилагаются вопросы, обсуждение ответов на которые позволяют уточнить некоторые особенности соответствующих моделей.

Предполагается, что обсуждение оптимизационных задач и их моделей позволяет не только познакомить студентов со способами формализации оптимизационных ситуаций, но и дает возможность студенту научиться строить алгоритм «понимания моделей», т.е. грамотно и адекватно формулировать свои вопросы по модели.

Нижеприведенные задачи классифицированы по классам моделей (линейного программирования, целочисленного программирования, нелинейного программирования, векторной оптимизации).

1.1.2. Примеры задач линейного программирования

Задача 1. 10. Планирование производства нефтепродуктов

В процессе переработки сырой нефти производится определенное количество бензиновых полупродуктов, которые затем последовательно смешиваются с целью получения других видов топлива для двигателей внутреннего сгорания – обычного топлива и топлива высшего качества [7]. Для каждого полупродукта известны значение показателя его эффективности, максимальный выход и фиксированная цена единицы объема полупродукта. Для каждого вида топлива установлены минимальное значение показателя эффективности и продажная цена, а также известны удельные затраты на смешивание топлива. Минимальный уровень производства обоих видов топлива определяется договорными обязательствами. Остальное произведенное топливо и неиспользованные полупродукты могут быть реализованы посредством свободной продажи по известным ценам. Требуется составить оптимальный план производства топлива в течение заданного периода времени.

На схеме, представленной на рис.1.2 , показано, что исследуемая система включает ряд бензиновых полупродуктов, технологическую операцию смешивания и два вида жидкого моторного топлива.

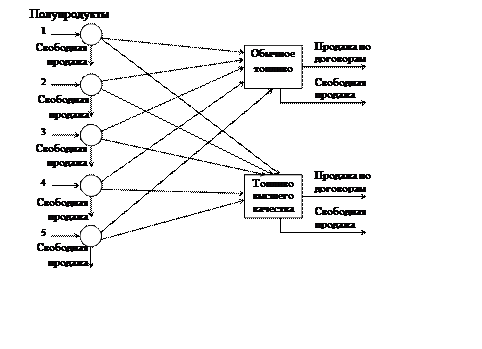
Рисунок1. 2 - Схема к задаче планирования нефтеперерабатывающего производства.

Критерием оптимальности функционирования системы в данном случае является чистая прибыль, реализуемая в течение планового периода. Чистая прибыль состоит из дохода от продажи топлива и полупродуктов за вычетом затрат на смешивание и производство полупродуктов. С каждым из полупродуктов ассоциированы три переменные. Одна из переменных выражает количество полупродукта, направляемого на производство обычного топлива, вторая – количество полупродукта, направляемого на производство топлива высшего качества, и третья – количество полупродукта, поступающего в свободную продажу.

Итак, для каждого полупродукта с номером i:

x_i – количество полупродукта, используемого для производства топлива обычного качества,

y_i – количество полупродукта, используемого для производства топлива высшего качества,

z_i – количество полупродукта, направляемого в свободную продажу.

С каждым видом топлива в свою очередь ассоциируются две переменные, одна из которых представляет количество топлива, продаваемого по договорам, а другая – количество топлива поступающего в свободную продажу.

Таким образом, для каждого вида топлива с номером j:

u_j – количество топлива, продаваемого по договорам,

v_j – количество топлива, поступающего в свободную продажу.

В модель следует включить соотношения для каждого полупродукта и каждого вида топлива, ограничения, связанные с технологической операцией смешивания и позволяющие учесть заданные уровни эффективности двух видов топлива, а также ограничения, вытекающие из наличия договорных обязательств.

Соотношение для полупродукта с номером i записывается в виде неравенства

,

где α_i –выход полупродукта i за плановый период.

Балансовые соотношения для конечной продукции имеют следующий вид:

.

Технологические ограничения, связанные с операцией смешивания, записываются в виде

,

где β_i – значение показателя эффективности для полупродукта i, а γ_j – минимальное значение показателя эффективности топлива вида j.

Ограничение, обусловленное договорными обязательствами, для топлива вида j задается неравенством

,

где δ_j – минимальный объем производства топлива j, предусмотренный договорами.

Критерий оптимальности функционирования системы (чистая прибыль) определяется выражением

,

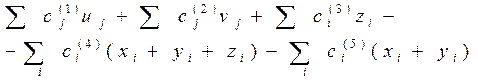где  – продажная цена единицы конечной продукции вида j в соответствии с договорами;  – рыночная цена единицы конечной продукции вида j;  – рыночная цена единицы полупродукта i;  – затраты на производство единицы полупродукта i;  – технологические затраты на смешивание в расчете на единицу полупродукта i.

Кроме того, все переменные должны принимать неотрицательные значения; в противном случае решение задачи может и не иметь «физической» интерпретации.

Вопросы для обсуждения:

1. Оцените размерность модели.

2. Сколько параметров в задаче?

3. Предложите метод решения полученной математической задачи, обоснуйте