




6. Программа на языке Pascal
Как следует из метода наименьших квадратов, при выборе аппроксиммирующих функций в виде полиномов математическое содержание решаемой задачи сводится к нахождению корней системы линейных алгебраических уравнений, порядок которой определяется выбором соответствующего полинома.
В данном фрагменте курсовой работы в соответствии с постановкой задачи приведена программа на языке Pascal, позволяющая определить аппроксимирующие полиномы первой и второй степени. Корни решаемых систем уравнений определяются в двух вариантах по способу Крамера и путем непосредственного решения соответствующей системы уравнений. Формулы, отражающие корни соответствующих систем уравнений получены с использованием символьного процессора пакета MathCad и приведены ниже.
Указание. Для того чтобы символьно решить конкретную систему уравнений относительно неизвестных используется функция Find. Сначала вводится с клавиатуры ключевое слово Given , затем – уравнения системы. Например, решение системы третьего порядка относительно неизвестных х1, х2, х3 осуществляется путем введения функции Find(х1,х2,х3) и ввода знака символьных вычислений (<Ctrl> + <.>) и щелчка по свободному месту рабочего документа.
Фрагмент рабочего документа MathCad с символьными вычислениями при непосредственном решении систем уравнений второго и третьего порядка имеет вид:
· определение корней системы второго порядка (вариант линейной аппроксимации)
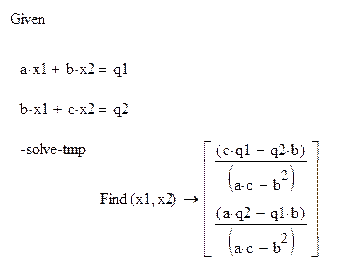
· определение корней системы третьего порядка (вариант квадратичной аппроксимации)
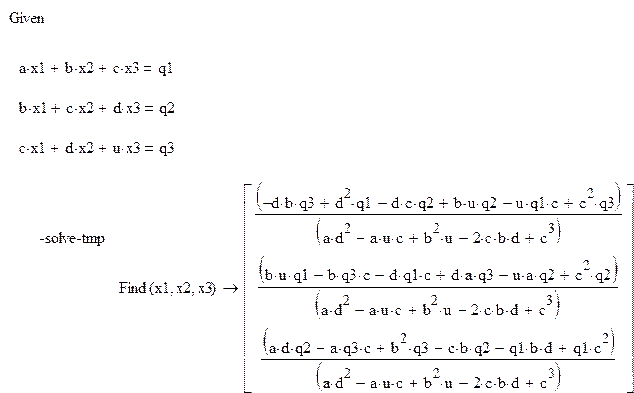
Фрагмент рабочего документа MathCad с символьными вычислениями при решении соответствующих систем уравнений методом Крамера имеет вид:
· определение корней системы второго порядка (линейная аппроксимация)
Корни имеют вид X1 = D1/D0, X2 = D2/D0, где D1 = q1*c – q2*b, D2 = q2*a – q1*b
D0 = a*c - b*b
· определение корней системы третьего порядка (квадратичная аппроксимация)
Корни имеют вид X1 = D1/D0; X2 = D2/D0; X3=D3/D0
D1 = q1*c*u + q2*c*d + q3*b*d – q1*d*d – q2*b*u – q3*c*c
D2 = q1*c*d + q2*a*u + q3*b*c – q1*b*u – q2*c*c – q3*a*d
D3 = q1*b*d + q2*b*c + q3*a*c – q1*c*c – q2*a*d – q3*b*b
D0 = a*c*u + b*c*d + b*c*d – c*c*c – b*b*u – a*d*d
Обратим внимание, что в решаемых системах уравнений (4) и (5) столбцы
свободных членов и коэффициенты при неизвестных кроме коэффициента находящегося
в первом уравнении при неизвестном ![]() являются суммами,
которые при написании программы будем вычислять по программной единице function
sum(x,y:mas_1_16;N,m,p:integer):real ориентированной на
вычисление суммы вида
являются суммами,
которые при написании программы будем вычислять по программной единице function
sum(x,y:mas_1_16;N,m,p:integer):real ориентированной на
вычисление суммы вида 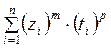 . Учитывая, что
значения изменения аргумента и заданной функции могут быть отрицательными и
равными нулю следовательно использование логарифмических зависимостей при
вычислении сумм приведет к некоторому увеличению алгоритма, поэтому при
вычислении входящих в общий член суммы сомножителей
. Учитывая, что
значения изменения аргумента и заданной функции могут быть отрицательными и
равными нулю следовательно использование логарифмических зависимостей при
вычислении сумм приведет к некоторому увеличению алгоритма, поэтому при
вычислении входящих в общий член суммы сомножителей ![]() и
и
![]() при написании программной единицы function sum(x,y:mas_1_16;N,m,p:integer):real
на языке Pascal воспользуемся традиционным алгоритмом,
используемом при создании фрагментов программ по вычислению произведений в
виде:
при написании программной единицы function sum(x,y:mas_1_16;N,m,p:integer):real
на языке Pascal воспользуемся традиционным алгоритмом,
используемом при создании фрагментов программ по вычислению произведений в
виде:
P:= 1;
For i:= 1 to n do
P:= p*q[i];
где q[i]
принимает значения ![]() и
и ![]() .
.
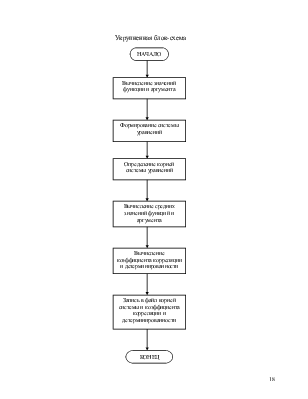
Ниже приведена блок-схема алгоритма и в приложении 1 программа на языке Turbo Pasсal. В приложении 2 отражено сопоставление результатов расчетов полученных в системе MathCad и Turbo Pascal.

7. Выводы
Данная курсовая работа посвящена определению аппроксимирующих полиномов заданной функции методом наименьших квадратов. Коэффициенты детерменированности близкие или равные единице и графики искомых функций позволяют удостовериться в том, что аппроксимирующие полиномы найдены верно. Наилучшая аппроксимация табличных данных получена при использовании кубического полинома, так как в этом случае коэффициент детерминированности наиболее близок к единице. Следовательно, кубический полином дает наилучшую аппроксимацию исходных данных.
Библиографический список
1.Богумирский Б.С. Norton Commander 5.0 Новые возможности для пользователя. СПб, 1995г.
2.Богумирский Б.С. MS-Dos 6.2/6.2: Новые возможности для пользователя. СПб, 1995г.
3.Нортон Питер Руководство по DOS Питера Нортона. М.:1995г.
4.Долголаптев В.Г. Работа в Exsel 7.0 для Windows 95 на примерах. М.: 1995г.
5.Зуев Е.А. Програмирование на языке Turbo Pascal 6.0; 7.0. Ь.: 1993г.
6.Ян Белицкий Turbo Pascal с графикой для персональных компьютеров. М.:1991г.
7.Потапкин А.В. Операционная система Windows 95. M.:1996г.
8.Рогов И.П. Microsoft Offis 97 М.: 1997г.
9.Кинг Адриан Windows 95 изнутри. СПб, 1995г.
10.Дженнигрс Р. Windows 95 в подлиннике. СПб, 1995г.
11.Вострикова З.П. Сервисная программа Norton Commander СПб, 1995г.
12.Смирнов В.В. Работа в MathCad 7 Professional. М.: 1999г
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.