Министерство образования Российской Федерации
Владимирский государственный университет
Кафедра конструирования и технологии радиоэлектронных средств
Лабораторная работа № 2
ОЦЕНКА ГЕНЕРАЛЬНЫХ ХАРАКТЕРИСТИК ПАРАМЕТРА КАЧЕСТВА ПО ВЫБОРОЧНЫМ ЗНАЧЕНИЯМ
Работу выполнил
студент гр. РЭ-100
Работу проверил
Владимир 2002
Цель работы. Изучение методов оценки генеральных характеристик по выборочным значениям.
Экспериментальные данные.
Значения первой выборки |
Значения второй выборки |
|
3.75 |
3.74 |
|
3.73 |
3.76 |
|
3.74 |
3.78 |
|
3.71 |
3.74 |
|
3.74 |
3.73 |
|
3.75 |
3.75 |
|
3.72 |
3.76 |
|
3.74 |
3.78 |
|
3.73 |
3.74 |
|
3.78 |
3.74 |
|
3.75 |
3.77 |
|
3.77 |
3.75 |
|
3.74 |
3.73 |
|
3.73 |
3.72 |
|
3.76 |
3.77 |
|
3.79 |
3.74 |
|
3.74 |
3.78 |
|
3.75 |
3.76 |
|
3.78 |
3.75 |
|
3.74 |
3.74 |
1. Определение доверительных интервалов для математического ожидания и дисперсии при объемах выборок 10,15,20(берутся по порядку).
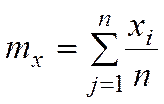 ;
; 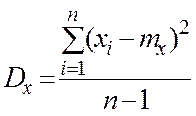 ;
;
Доверительный интервал для математического
ожидания ![]() находится по неравенству
находится по неравенству
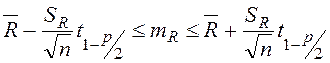 , где
, где ![]() ,
,![]() — среднее арифметическое и номинальное
значение в выборке;
— среднее арифметическое и номинальное
значение в выборке;
![]() —
объем выборки (задается преподавателем);
—
объем выборки (задается преподавателем);
![]() — уровень значимости;
— уровень значимости;
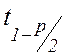 —
квантиль распределения Стьюдента, определяемый по уровню
значимости
—
квантиль распределения Стьюдента, определяемый по уровню
значимости ![]() и
числу степеней свободы (Таблица П4).
и
числу степеней свободы (Таблица П4).
Доверительный интервал для дисперсии при нормальном законе распределения равен
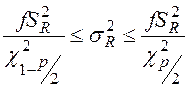
где ![]() —
выборочная дисперсия;
—
выборочная дисперсия;
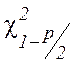 ,
, 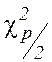 —
квантили распределения Пирсона, определяемые из таблицы П2 по уровню
значимости
—
квантили распределения Пирсона, определяемые из таблицы П2 по уровню
значимости ![]() и
числу степеней свободы .
и
числу степеней свободы .
Расчетные и экспериментальные данные представлены в таблицах
1.1. Математическое ожидание и дисперсия для различных выборок.
|
Размер выборки |
Выборка №1 |
Выборка №2 |
||
|
Математическое ожидание |
Дисперсия |
Математическое ожидание |
Дисперсия |
|
|
10 |
3,739 |
0,000366 |
3,752 |
0,000307 |
|
15 |
3,743 |
0,000335 |
3,751 |
0,00035 |
|
20 |
3,747 |
0,000422 |
3,753 |
0,000319 |
1.2. Значения доверительного интервала для математического ожидания.
|
Значение выборки |
Доверительная вероятность |
|||
|
0,8 |
0,95 |
0,99 |
||
|
Доверительный интервал для математического ожидания |
10 |
2.437 |
1.695 |
1.035 |
|
15 |
1.49 |
1.075 |
0.67 |
|
|
20 |
1.073 |
0.784 |
0.499 |
|
1.3. Значения доверительного интервала для дисперсии.
|
Значение выборки |
Доверительная вероятность |
|||
|
0,8 |
0,95 |
0,99 |
||
|
Доверительный интервал для дисперсии |
10 |
0.00027 |
0.00021 |
0.00015 |
|
15 |
0.00022 |
0.00017 |
0.00012 |
|
|
20 |
0.00016 |
0.00011 |
0.00008 |
|
При увеличении значения доверительной вероятности увеличивается доверительный интервал как для математического ожидания, так и для дисперсии, но с увеличением выборки он уменьшается.
2.
Сравнение дисперсии и математических ожиданий выборок. ![]()
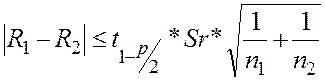 ,
,
2.1. Сравнение двух средних.
|
Значение выборки |
Доверительная вероятность |
|||
|
0,8 |
0,95 |
0,99 |
||
|
|
10 |
0.013<2.32 |
0.013<3.98 |
0.013<5.8 |
|
15 |
0.008<1.62 |
0.008<2.98 |
0.008<4.19 |
|
|
20 |
0.006<1.58 |
0.006<2.5 |
0.006<3.44 |
|
Из таблицы видно, что условие сравнения средних выполняется. При увеличении доверительной вероятности выполнения условия сравнения средних становится более затруднительным.
2.2. Сравнение дисперсии.
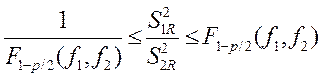
0.35<1.093<2.85
0.45<1.260<2.2
0.42 <1.153<2.35
 Так как
выполняются эти неравенства, то можно считать эти дисперсии равными.
Так как
выполняются эти неравенства, то можно считать эти дисперсии равными.
Вывод: в результате проделанной работы были рассчитаны доверительные интервалы для математических ожиданий и дисперсий трех выборок при различных значениях доверительной вероятности. Было проведено сравнение дисперсий и математических ожиданий, которое показало, полученные дисперсии удовлетворяют критерию Фишера, следовательно, их можно считать равными генеральной дисперсии; полученные математические ожидания проверены с помощью метода сравнения двух средних, они удовлетворяют этому условию.
|
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.