Теоретические подходы при создании ЭС различной степени сложности, страница 3

3. ПОИСК ОПТИМАЛЬНЫХ ПАРАМЕТРОВ И ЭКСТРЕМУМА ЦЕЛЕВОЙ ФУНКЦИИ.

Задание: предприятие должно выпустить два вида продукции, используя последовательно четыре различных группы производственного оборудования. Выпуск одного комплекта продукции вида А обеспечивает прибыль в два миллиона рублей, продукции вида В – три миллиона рублей. Месячный фонд времени, в днях, каждой группы оборудования и трудоёмкость, также в днях, для изготовления комплектов продукции А и В представлены в таблице.

Разработать план производства, который обеспечит наибольшую прибыль для предприятия.

Решение.

Таблица 3 - Исходные данные

Группа оборудования	Норма времени на выпуск одного комплекта		Фонд времени
	А	В
I	4,3	4,3	16,3
II	3,3	4,7	18
III	2,7	1,3	16
IV	2,3	3,3	9,3

Пусть x₁ - количество комплектов продукции вида А, а x₂ - количество комплектов продукции вида В. Эти переменные являются положительными независимыми параметрами, для определения которых необходимо составить целевую функцию f(x₁, x₂) и функции связи (функции ограничения):        

П = f(x₁, x₂) = 2000000×x₁ + 3000000×x₂ ;

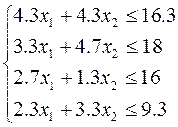
1.  x₁=0        x₂=3.8  

x₁=3.8     x₂=0                                        

2.   x₁=0       x₂=3,8

x₁=5,5    x₂=0

3.  x₁=0        x₂=12,3                    

x₁=5,9     x₂=0                         

4.  x₁=0        x₂=2.8

x₁=4,0     x₂=0

Необходимо найти x_i при заданных ограничениях, которые определяют экстремум целевой функции.  Для этого строится график зависимости x₂(x₁) (рис.4), отражающий область возможных значений.

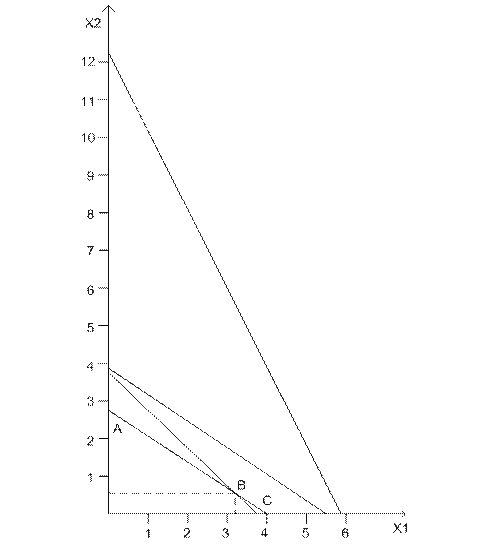
Рис. 4 Область возможных значений

Для определения максимума определяются значения целевой функции в точках А(0; 2,8), В(3,2; 0,55) и С(3,8;0).

 П_А = 2000000×0 + 3000000×2,8 =8400000;

  П_В = 2000000×3,2 + 3000000×0,55 =8050000;

  П_С = 2000000×3,8 + 3000000×0=7600000.

Максимума функция достигает в точке А, что соответствует параметрам  x₁ = 0;  x₂= 2,8. Поскольку количество комплектов продукции должно быть четным числом  надо округлить x₂.

Пусть x₂=3, а x₁ = 0, тогда:

4.3∙0+ 4.3∙3≤16

12,9≤16  верно          

3.3∙0+4.7∙3 £18

14,1≤18  верно

2.7∙0 +1.3∙3 ≤16

3,9≤16 верно

2.3∙0+3.3∙3£9.3

9,9≤9,6 неверно

4-е условие не выполняется, значит необходимо округлять x₂ до 2.

Проверка:

4.3∙0+ 4.3∙2≤16

8,6≤16  верно                

3.3∙0+4.7∙2 £18

9,4≤18  верно

2.7∙0 +1.3∙2 ≤16

2,6≤16 верно

2.3∙0+3.3∙2£9.3

6,6≤9,6 верно

Если предприятие будет выпускать 2 комплекта продукции вида В, то его прибыль будет равна:

П_А = 2000000×0 + 3000000×2= 6000000.

Был разработан план производства, который обеспечивает наибольшую прибыль предприятия. При использовании данного плана предприятие должно выпускать 2 комплекта продукции  вида В, при этом его прибыль будет равна 6000000 руб.  

ЗАКЛЮЧЕНИЕ

Особенностью  проблемы  надежности  является  ее  связь  со  всеми   этапами жизненного цикла РЭС от зарождения идеи создания до списания: при  расчете и  проектировании  изделия  его  надежность  закладывается  в  проект,   при изготовлении надежность  обеспечивается,  при  эксплуатации  -  реализуется. Поэтому проблема надежности - комплексная проблема и  решать  ее  необходимо на всех  этапах  и  разными  средствами.  На  этапе  проектирования  изделия определяется его структура, производится  выбор  или  разработка  элементной базы, поэтому здесь имеются наибольшие  возможности  обеспечения  требуемого уровня  надежности  РЭС.  Основным  методом  решения  этой  задачи  являются расчеты надежности (в первую очередь  -  безотказности),  в  зависимости  от структуры объекта и характеристик его  составляющих  частей,  с  последующей необходимой  коррекцией  проекта, определение максимальной прибыли с учетом затрат времени и трудоемкости и другие немаловажные факторы влияющие на стоимость и качество РЭС.

 СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ

1.  Теоретические основы конструирования, технологии и надежности РЭА: Методические указания к курсовой работе / Е.Н. Талицкий Владим. гос. ун-т. Владимир, 1987.

2.  Яншин А. А. Теоретические основы конструирования, технологии и надежности ЭВА

3.  Автомобильный автоматический КСВ-метр, И. Нечаев / Радио, 2005, №6 – с.68

4.  Методические указания к лаб. работам: Механические воздействия и защита РЭА/Под ред. Е.Н. Талицкого - Владимир,1982.36с.