ОГЛАВЛЕНИЕ
Введение……………….………………….……………………………………….2 1. Расчет допусков замыкающего звена детали...………………………3 2. Расчет вероятности безотказной работы ………………………………8 3. Поиск оптимальных параметров и экстремума целевой функции……12 Заключение…………….………………….……………………………………...16
Список использованной литературы……………………………………….17
ВВЕДЕНИЕ
На современном этапе развития электронной техники все большее значение приобретают теоретические подходы при создании ЭС различной степени сложности, т.к. позволяют быстрее и с лучшим качеством создавать современную аппаратуру общего и специального назначения. Поэтому знать теоретические основы создания ЭС необходимо, т.к. вопросы конструирования, разработки технологии и обеспечения надежности РЭС имеют большое значение в настоящее время.
При высокой сложности аппаратуры использование удовлетворительных конструкторских и технологических решений уже не представляется возможным, и необходимо искать решения, близкие к оптимальным. Установить такие решения опытным путем практически невозможно; они могут быть получены лишь на основании теоретического анализа.
По своей математической постановке технологические задачи схожи с конструкторским0и, и для их решения используют те же математические методы, что и для решения конструкторских задач.
С развитием микроэлектроники сложность процесса создания ЭС усложняется прежде всего в теоретическом плане, поэтому необходимо знать математические методы, используемые для анализа, синтеза и оптимизации процессов конструирования и технологии производства ЭС с целью повышения его качества.
1. РАСЧЕТ ДОПУСКОВ ЗАМЫКАЮЩЕГО ЗВЕНА ДЕТАЛИ
Задание: рассчитать предельные отклонения замыкающего звена, показанного на рисунке 1, для размеров составных звеньев А1=90-0,4 А2=40-0,2 А3=30±0,1 аi=0.2 ki=1.15. Расчет выполнить методами предельных отклонений и вероятностным.
Решение.
В соответствии с заданием составляется размерная цепь (рис.1).
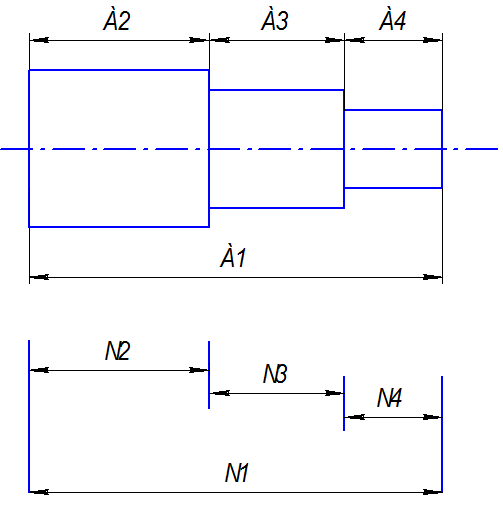
Рис. 1 Размерная цепь
Звено А1 увеличивающее, звенья А2, А3 уменьшающие, звено А4 замыкающее.
Данные по звеньям сведены в таблицу 1.
Таблица 1 - Данные по звеньям
|
Звено |
Номинальный размер, Ni |
Отклонение середины поля допуска от номинального значения, Еi |
Половина поля допуска, δi |
|
А1 |
90 |
-0,2 |
0,2 |
|
А2 |
40 |
-0,1 |
0,1 |
|
А3 |
30 |
0 |
0,1 |
Предельные отклонения имеют три составляющие:
![]() , (1)
, (1)
где ![]() -
номинальное значение параметра,
-
номинальное значение параметра, ![]() - отклонение середины
поля допуска от номинального значения,
- отклонение середины
поля допуска от номинального значения, ![]() -
половина поля допуска.
-
половина поля допуска.
Для метода предельных отклонений:
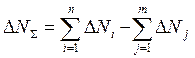 , (2)
, (2)
где N=n+m,
N – количество составляющих звеньев, n – количество увеличивающих звеньев (коэффициент влияния для увеличивающих звеньев -1), m – количество уменьшающих звеньев (коэффициент влияния для уменьшающих звеньев -1).
С учетом этого:
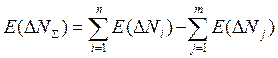 (3)
(3)
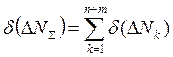 . (4)
. (4)
Для применения вероятностного метода необходимо установить связь между характеристиками поля допуска. Такая связь описана следующим выражением уравнением Бородачева:
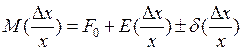 ял допуска формула
ял допуска формула
Тогда эти выражения принимают вид:
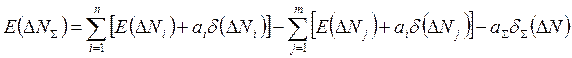 , (5)
, (5)
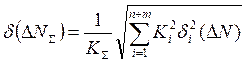 , (6)
, (6)
где а – коэффициент относительной асимметрии распределения отклонений в поле допуска, К – коэффициент относительного рассеивания, определяемые по формулам:
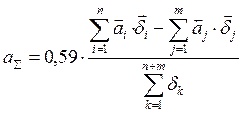 , (7)
, (7)
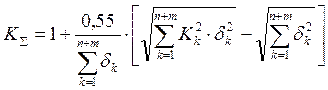 (8)
(8)
Расчет допусков замыкающего звена детали А4.
1. Расчет номинального размера замыкающего звена:
N4= N1-N2-N3=94всет (7вания, определяемыйицу1.ялонений и вероятностным методомсунке 1, для размеров составных зеньев0-40-30=20.
2. Расчет допусков замыкающего звена методом предельных отклонений (4), (5):
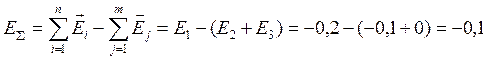
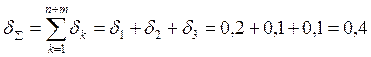
![]()
3. Расчет коэффициента относительной асимметрии аΣ и коэффициента относительного рассеивания КΣ (7), (8):
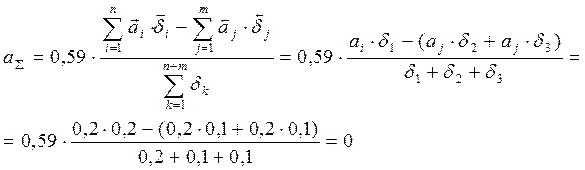
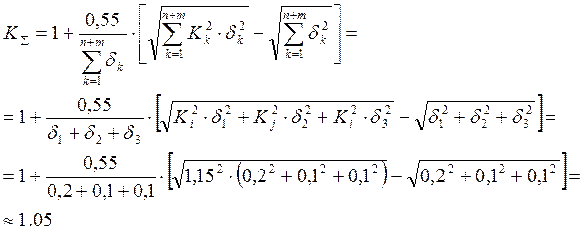
4. Расчет допусков замыкающего звена вероятностным методом (5), (6):
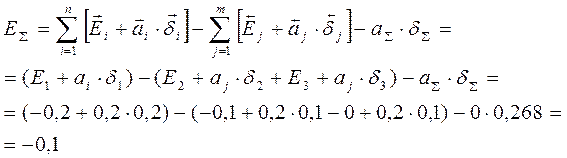
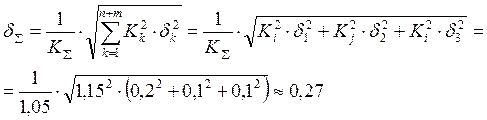
![]()
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.