Физика \ Электроника

Расчет точности детали. Предельные отклонения замыкающего звена детали, страница 2

Рассчитываем λ интенсивность отказов схемы РЭА, по формуле:

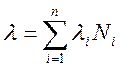    , где n – число типов элементов, работающих в одинаковых условиях.

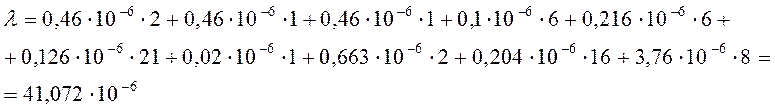
Вероятность безотказной работы:

        


        λ


   t

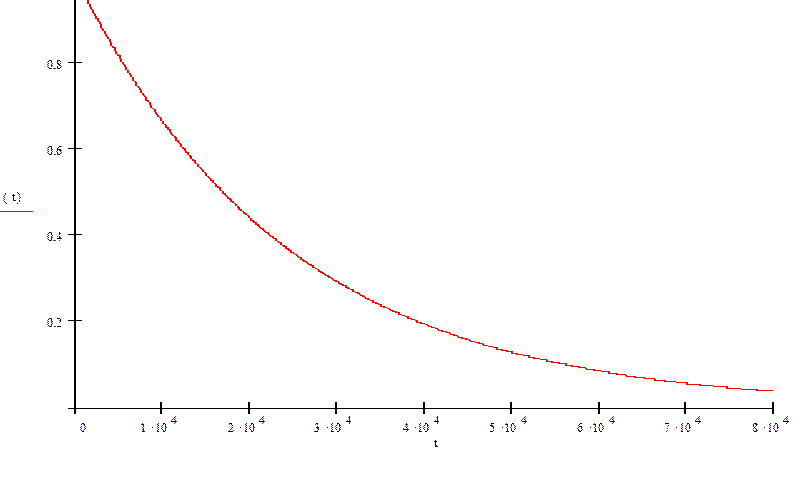
Рис. 4. График вероятности безотказной работы.

Находим среднюю наработку на отказ:

      

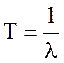
Вывод: в ходе опыта было определено, что вероятность безотказной работы составляет λ = 41,072·10-6, и средняя отработка на отказ Т = 24347. Полученные значения говорят о надежности данной схемы, как и у любой схемы надежность работы уменьшается с ростом времени работы схемы, что наглядно видно на графике вероятности безотказной работы.


3.НАХОЖДЕНИЕ ОПТИМАЛЬНЫХ ПАРАМЕТРОИ ЭКСТРЕМУМА ЦЕЛЕВОЙ ФУНКЦИИ МЕТОДОМ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ.

Предприятие должно выпустить два вида продукции, используя последовательно четыре группы производственного оборудования. Выпуск одного комплекта продукции вида  А обеспечивает прибыль - 2 млн. руб., а продукции вида В - 3 млн. руб. Ежемесячный фонд времени ( в днях ) для изготовления комплектов продукции вида А и В представлен в таблице 1. Разработать план производства, который обеспечивает наибольшую прибыль предприятия.

Группа оборудования

Норма времени на выпуск одного комплекта продукции

Фонд времени

А

В

I

5,2

5,2

17,2

II

4,2

3,8

18

III

1,8

2,2

16

IV

3,2

4,2

10,2

Составим целевую функцию:

X1-количество компонентов продукции типа А;

X2-количество компонентов продукции типа B.

Общее уравнение:    y=2x1+3x2

Уравнение ограничений:

5,2 x 1 + 5,2 x2 ≤ 17,2;

4,2 x1 + 3,8 x2 ≤ 18;

1,8 x1 + 2,2 x2 ≤ 16;

3,2 x1 + 4,2 x2 ≤ 10,2.

где: x1≤0;  x2≤0.

Решение сводится к задаче линейного программирования. Необходимо найти вершины многоугольника.

1)

2)

3)

4)

x1=3,3   x2=0

x1=4,3   x2=0

x1=8,9   x2=0

x1=3,2   x2=0

x1=0   x2=3,3

x1=0   x2=4,7

x1=0   x2=7,3

x1=0   x2=2,4


            Х1       

                10

9

8

7

6  

5

4

3

2

1

1     2      3      4     5      6      7     8      9     Х2                 

Рис.5

Из рис.5. 

x1=3,3   x2=0

x1=0   x2=2,4

тогда                                   

у1=3,3∙2+0∙3=6,6

у2=0∙2+2,4∙3=7,2

но вследствие того, что продукция выпускается только целыми величинами, округлим полученные значения до ближайшего целого числа:

x1=3; x2=2.

Проверим полученные числа на удовлетворения неравенствам

5,2 x 1 + 5,2 x2 ≤ 17,2;

4,2 x1 + 3,8 x2 ≤ 18;

1,8 x1 + 2,2 x2 ≤ 16;

3,2 x1 + 4,2 x2 ≤ 10,2.

1)

2)

3)

4)

x1=15,6   x2=0

x1=12,6   x2=0

x1=5,4   x2=0

x1=9,6   x2=0

x1=0      x2=11

x1=0     x2=7,6

x1=0   x2=4,4

x1=0   x2=8,4


x1=3     x2=0;

x1=0     x2=2.

тогда

y1=3∙2+0∙3=6;

y2=0∙2+2∙3=6.

Производственный план: Для того чтобы предприятие получило прибыль в 6 млн. руб. нужно выпускать продукцию вида А или В в зависимости от того, на что выше спрос.

Вывод : при выполнении данного задания был разработан план производства, который обеспечивает наибольшую прибыль предприятия. При использовании данного плана предприятие должно выпускать продукцию, которая пользуется наибольшим спросом.


Список используемой литературы:


1.  Справочник конструктора РЭА: Общие принципы конструирования/Под руководством ред. Р.Г. Варламова.-М.:Сов.радио,1980.-480с.,ил. 

2.  Методические указания к лаб.работам: Механические воздействия и защита РЭА/Под ред. Е.Н. Талицкого.-Владимир,1982.- 36с.,ил.

3.  А.А. Яншин Теоретические основы конструирование, технологии и надежности ЭВА: Учеб. Пособие для вузов. – М.: Радио и связь, 1983. – 312с.

 

Скачать файл