Об`єкт, предмет та задачі дисципліни. Вихідні поняття та суть економічного прогнозування

таким чином виключається сезонна складова; щод дати оцінку сезонній складовій S^ слід розділити Y_t на Y_t’ (без сезонного фактору).

Для одержання оцінки тренду слід побудувати модель тренду. Припустимо, що тренд має лінійну модель, тобто Y_t’=T_t*I_t=a+b*t+U_t; за МНК Y_t’^=126,52+1,83t

Ця модель непогано описує дійсність. Випадкова складова І=1. Оскільки дані спостереження Y_t’ починаються з третього квартала 1981 р., також дану модель можна розгядати за допомогою МНК (експоненційна залежність)

ln Y_t = ln a₀+l*t+a₁*q₁*t+a₂*q₂*t+a₃*q₃*t+U_t

q₁, q₂, q₃ – штучні змінні, показують вплив на У певного кварталу. Ці змінні мають специфіку: змінна q₁ приймає значення 1 в першому кварталі, q₂ – в другому кварталі, q₃ – в третьому кварталі. Коли всі змінні дорівнюють 0 – четвертий квартал.

Кв-л	q1	q2	q3
I	1	0	0
II	0	1	0
III	0	0	1
IV	0	0	0

Для інформації про всі квартали досить 3-х змінних.

Отримані а1^ – показує наскільки зв’язані між собою І та IV квартали

a₂^ – між II i IV

a₃^ – між III i IV

a₁^ – оцінка Ш кварталу, коли всі інші не впливають на І і т.д.

Щоб визначити окремо вплив кожного кварталу на І, треба побудувати модель, прирівнюючі змінні q до 0 і залишивши лише ту змінну, що відповідає певному кварталу. Наприклад, якщо ми хочемо показати вплив І кварталу, тоді q₂, q₃=0, модель має вигляд: ln a₀ + l*t + a₁*q₁*t

3. Метод рухомого середнього та його особливості

Метод рухомого середнього – усереднює n попередніх значень (фактичних значень показника У) і видає його як прогноз на t+1  період. Прогнозне значення,

n –  степінь рухомого середнього

Рухоме середнє 5-го порядку: F_t+1=1/5*(y_t+y_t-1+y_t-2+y_t-3+y_t-4)

Недоліки методу:

1) всім спостереженням дається однакова вага, але більш свіжі дані важливіші для прогнозу, тобто мають більш вагу.

2) Крім того, ряд не має історії, обриває спостерження.

3) при появі нового числа, треба перераховувати весь прогноз.

Можна зменшити недоліки:

F_t+1 =0,4*y_t+0,3*y_t-1+0,2*y_t-2+0,1*y_t-3 – вага спадає при старінні даних.

4. Метод експоненційного згладжування

Недоліків методу рухомого середнього немає у методі експоненційного згладжування.

Метод експоненційного згладжування – найбільша вага надається найближчому спостереженню, а потім вага всіх спостережень спадає в геометричній прогресії.

Вага спостережень спадає в такому порядку:

a+ a*(1-a) + a*(1-a)²

Прогноз на t+1 період: F_t+1 = a*Y_t + (1-a)*E_t,

Тобто в сумі ці коефіцієнти дають 1.

Або F_t+1 = F_t + a*(Y_t - F_t) = F_t + a*e_t, де (Y_t - F_t) – похибка прогнозу

a – кореляція похибки, вона визначає швидкість старіння даних, або швидкість, з якою новий прогноз пристосований до похибки. Якщо a=0 – пристосування до похибки немає, a=1 – повне пристосування до похибки. Звичайно, aбереться в цифрах: a=[0,05; 0,01; 0,02; 0,03]. Але якщо ми нехтуємо дуже великими рядами, і хочемо, щоб проноз був чутлим до свіжих даних, тоді a=0,7 і більше.

Тобто, якщо чутливість прогнозу до даних велика (реагує на всі нові спостереження), тоді a прямує до 1. Якщо хочемо, щоб прогноз був нечутливим до змін даних, тоді a менше 0,3.

Переваги:

1) при появі нових даних не треба перераховувати всю схему спочатку, для одержання наступного значення прогнозу слід знати поточне значення попереднього спостереження y_t і прогнозне його значення на час t: y_t^.

Якщо порівняти ці 2 методи

(n-1)/2 = (1-a)/2 – це співвідношення показує, що чутливість методу рухомого середнього залежить від довжини ряду, а чутливість методу експотенц. згладжування – тільки від a. Прирівняємо і отримаємо, що

a	0,05	0,1	0,2	0,3
n	39	19	9	6

Для методу експот. зглад. – важливо встановити:

1) параметр a;

2) визначити довжину ряду, що згладжується;

3) визначити початкове значення (F₀) прогнозу

F₁ = a*y₁ + (1-a)*F₀, де y₁ – поточне значення. Тому важливо знати значення F₀.

Для цього існує кілька шляхів:

1) методом рухомого середнього знайти це значення з кількох попередніх спостережень

2) якщо ряд не має тренду, F0 можна прирівняти до у^--;

3) F₀ = y₁ при F_t+1 = a*y_t + (1-a)*F_t

Вибір a – залежить від даних. При аналізі даних сталої економіки – менш чутливий прогноз, великі ряди спостережень, a менше 0,3. При несталих процесах – менші ряди, a – велике.

Довжина бази прогнозу – пов’язана з вибором великих a. Крім цього, якщо ряд великий, то вибір початкового значення F₀ стає не принциповим.

Розглянемо експериментальний метод (метод експертної виборки): спочатку задаємо a, наприклад, a=0,05.

Дані спостережень ділимо на 2 частини: перша – дані, за якими буде розрахована прогнозна функція; 2 – експериментальні, за якими буде визначена якість прогнозу.

1 частина : у₁...у_k              2 частина:  y_k+1 ...y_n

Методом експ. згладж. визначимо прогноз F_k+1 за даними І частини. При цьому F₀ визначається як рухоме середнє 3-го порядку: F₀ = (y₁ + y₂ + y₃)/3  або просто F₀=y₁.

Визначимо помилки прогнозу: е₁=y_k+1 - F_k+1

Далі ряд спостережень (І част.) зсуваємо на 1: у₂, у₃, ..., у_k+1. На його основі визначаємо прогноз F_k+2 і розраховуємо похибку прогнозу e₂ = y_k+2 - F_k+2. В результаті отримаємо n-k похибок і зможемо розрахувати якість прогнозу за одним із показників:

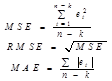
Потім, змінюючи значення a=0,1, повторюємо процедури. Так для всіх a (поки не =1). Потім порівнюємо показники якості, вибираємо найкраще a.

На основі методу експотенц. зглад. можна розрхувати і похибки прогнозу. Наприклад, МАЕ_t+1 = a*|e_t| + (1-a)MAE

Метод рухомого середнього має різні модифікації: метод Ханта, метод подвійного згладжування Брауна, метод Холта-Вінтера, метод Бокса - Дженкінса – застосовуються для визначення авторегресійних функцій і тому будуть розглянуті пізніше.

5. Вибір характеристик згладжування

Для методу експоненційного згладжування  важливо правильно вибрати характеристики:

1) параметр a;

2) визначити довжину ряду, що згладжується;

3) визначити початкове значення (F₀) прогнозу

1) Вибір a – залежить від даних. При аналізі даних сталої економіки – менш чутливий до нових даних прогноз, великі ряди спостережень, a менше 0,3. При несталих процесах – менші ряди, a – велике.

Якщо a=0 – пристосованності до похибки нема; якщо a=1 – пристосованість до похибки повна. зазвичай a береться в діапазоні [0,05;0,3]. Але якщо ми хочемо, щоб прогноз був чутливим до свіжих даних, тоді a береться в діапазоні [0,6;0,9]. Тобто, якщо чутливість прогнозу велика (реагує на всі нові спостереження), то aÞ1.

2) визначити довжину ряду згладжування:

Довжина бази прогнозу – пов’язана з вибором великих a. Крім цього, якщо ряд великий, то вибір початкового значення F₀ стає не принциповим.

3) F₁ = a*y₁ + (1-a)*F₀, де y₁ – поточне значення. Тому важливо знати значення F₀.

Для цього існує кілька шляхів:

1) методом рухомого середнього знайти це значення з кількох попередніх спостережень

2) якщо ряд не має тренду, F0 можна прирівняти до у^--;

3) F₀ = y₁ при F_t+1 = a*y_t + (1-a)*F_t

6. Економетричне прогнозування

Економетричні методи – базуються на правильно побудованій економетричній моделі – є каузальною (роз’яснює змінення у не просто в часі, а як функцію від інших економічних показників – причинно-наслідкові зв’язки між економічними показниками).

Етапи прогнозування:

1. постановка задачі

2. побудова матем. моделі (залежності)

3. збір та вивчення необхідної інформації

4.оцінювання параметрів моделі з метою встановлення її відповідності попереднім припущенням з етапу 2

5.якщо передумови моделі не виконуються, змінюється специфікація моделі або застосовуються інші методи оцінювання її параметрів

6. після того, як знайдено відповідну теоретичну модель, зробити верифікацію моделі, з’ясувати її прогнозні властивості

Вимоги до моделі:

1) модель відповідає теоретичним гіпотезам економіки, які підтверджуються даними спостережень

2) оцінені параметри моделі повинні бути статистично значимими

3) прогнозні властивості моделі повинні задовольняти як статистичним показникам якості (стандартна похибка) так і економічній теорії

І етап – постановка задачі – треба добре розумітись на предметній області

ІІ етап – побудова мат. моделі. Мат. модель має певну специфікацію. Найбільш проста модель: y_t=a₀+a₁*x_t1+a₂*x_t2+... +a_k*x_tk+U_t – регресія у – залежна змінна; х – параметр

y_t= f(x_t)+U_t – закон розподілу випадкової величини

Припускаємо, Е(U_t) = 0, Е(U_t,U_t+t)=0  при t ¹0, а при t = 0, Е(U_t,U_t+t)=(s _u)² = const (нормальний закон розподілу).

Також : х не залежні, тобто не корелюють між собою та з випадковимою вел-ною U.

Економетр. моделі можуть складатись з систем рівнянь (наз. системи одночасних рівнянь). Розглянемо для прикладу спрощену модель Кейнса. Дана модель розглядає економіку на макрорівні; при цьому нас цікавить залежність нац. доходу від інших показників,

Y_t=C_t+I_t+G_t   (відповідно споживання, інвестиції, держ. витрати)

В таких моделях змінні поділяються на екзогенні (задаються поза моделлю) та ендогенні (значення яких визначаються за допомогою моделі). В нашій моделі: Y_t – ендогенна; C_t – ендогенна, повинна бути включена в модель.

Спрощено: C_t =a₀+a₁(Y_t-T_t)+U_1t, де Y_t – доходи, T_t – податки.

I_t=b₁*Y_t-1+b₂*R_t+U_2t, де Y_t – капітал, R_t – відсоткова ставка.

G_t,T_t, R_t – екзогенні змінні (спрощено)

M1 – касові залишки

Від R_t залежать М1, також М1 залежать від Н_t, інші залежності, але ми поки що від них відмовимось.

Y_t-1 – лагова ендогенна змінна – вважаємо, що на період t це значення буде відомо, тому вважаємо її наперед визначеною, вона відноситься до пояснюючих змінних.

Для розрахунку параметрів структурної форми моделі використовується приведена форма, коли кожна ендогенна змінна виражається тільки через наперед визначені змінні (екзогенні або лагові).

В наведеній формі рівнянь стільки, скільки є невідомих. Коефіцієнти в цих рівняннях відповідають економічним мультиплікаторам. Щоб отримати приведену форму, зробимо підстановки.

Y_t=a₀/(1-a₁)+b₁/(1-a₁)*Y_t-1+b₂/(1-a₁)*R_t+1/(1-a₁)*G_t–a₁/(1-a₁)*T_t+E₁

Ct=a₀/(1-a₁)+{a₁*b₁/(1-a₁)*Y_t-1+(a₁*b₂/(1-a₁)}*R_t+a₁/(1-a₁)*(G_t-T_t)+E₂

I_t=b₁*Y_t-1+2*R_t+E₃

Для нац. доходу (1) розглянемо коеф-т при G_t:

1/(1-a₁)=1/(1-0,6)=2,5 – мультиплікатор

a₁ – коеф-т граничного споживання, a1»0,6 – на світовому рівні.

Якщо G_t зросте на 1, тоді Y_t зросте на 2,5

Економетр. модель в приведеній формі дозволяє визначити параметри a та b, а також має екон. зміст.

Всі макромоделі будуються як системи. Перед тим, як розв’язувати параметри структурної форми моделі, слід визначити, чи є окремі рівняння моделі ідентифікованими, чи ні. Якщо рівняння не ідентифіковані, не знайдемо вірну модель.

Якщо в рівнянні кількість пропущених екзогенних та ендогенних змінних дорівнює кількості ендогенних змінних