Реализация логической функции на мультиплексоре 8/1

          Цель работы.

Ознакомление с основными схемотехническими представлениями комбинационных цифровых устройств (далее по тексту – КЦУ). Изучение способов реализации с помощью типового КЦУ логической функции , принимающей значение "1" на наборе [1, 2, 4, 8, 11, 12, 13, 14, 15]. Синтез цифровых комбинационных схем на основе типовых КЦУ.

Таблица 1. Таблица истинности ЛФ y.

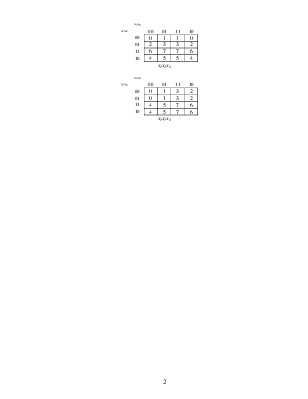
Реализуем заданную ЛФ четырех переменных с помощью мультиплексора 8/1. На три адресных входа такого мультиплексора можно подать три из четырех переменных x₃x₂x₁x₀. Этими тремя переменными будет задаваться адрес входного канала мультиплексора D_i(0…7). Клетки диаграмм Вейча четырех переменных нумеруются числами от 0 до 15. Аналогично можно пронумеровать клетки диаграмм Вейча адресами каналов i мультиплексора, не учитывая четвертый аргумент. Таких диаграмм будет четыре – по числу возможных сочетаний из 4 аргументов по 3. Диаграммы представлены ниже.

Таким образом, числа i (номера каналов) разбили указанные диаграммы Вейча на 8 частей, каждая из которых представляет диаграмму Вейча из двух клеток для одного аргумента, не являющегося адресным, соответственно x₃, x₂, x₁, x₀. Эти восемь диаграмм Вейча одной переменной определяют функции D_i = φ_i(x_j), которые надо подать на входы мультиплексора. Результаты приведены в таблице 3.

Таблица 3.

Предпочтение следует отдать той схеме, на информационные входы которой подается большее число констант 1 и 0. Выберем для реализации последний вариант, когда на адресные входы мультиплексора 8/1 подаются аргументы x₃x₁x₀. Представим принципиальную схему.

начертим принципиальную схему;

Рисунок 1. Принципиальная схема КС на базе мультиплексора.