Построение интегральной кривой стока в прямоугольной и косоугольной системах координат по среднемесячным расходам реки Черемшан. Построение гистограммы и статистической кривой обеспеченности максимальных годовых расходов реки Сок

Санкт-Петербургский государственный политехнический университет

Инженерно-строительный факультет

Кафедра «Инженерные мелиорации, гидрология и охрана окружающей среды».

Инженерная гидрология

Курсовой проект

Выполнил студент группы 3012/3 Саква О.С..

Проверила доц. Скворцова О.С.

                          «________»_________________________2009 г.

Санкт-Петербург

2009

Оглавление

1.      Построение интегральной кривой стока в прямоугольной и косоугольной системах координат по среднемесячным расходам реки Черемшан

2.      Построение гистограммы и статистической кривой обеспеченности максимальных годовых расходов реки Сок

3.      Построение математической и эмпирической кривых обеспеченности максимальных годовых расходов реки Сок

4.      Вычисление коэффициента корреляции между максимальными наблюденными расходами рек Сок  и Черемшан и удлинение ряда наблюдений

5.      Определение максимальных расчетных расходов для реки Сок при условии строительства гидротехнического сооружения I класса капитальности

Список литературы

1.  Построение интегральной кривой стока в прямоугольной и косоугольной системах координат по среднемесячным расходам реки Черемшан

ИКС в прямоугольной системе координат

Сток W определяется интегрированием расхода Q по времени:

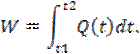
Однако, функция Q=f(t) неизвестна, поэтому величина стока определяется методом прямоугольников:

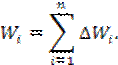
Свойства ИКС:

1)  Функция W=f(t) – неубывающая.

2)  Точка перегиба на ИКС соответствует Qmax или Qmin на гидрографе. Выпуклость кривой вверх отвечает уменьшению расхода на гидрографе, вниз – увеличению.

3)  Тангенс угла наклона прямой, соединяющей начало и конец ИКС, пропорционален среднему многолетнему расходу.

Построения ИКС в косоугольной системе координат выполнены на рис. 1.

Для удобства построения кривой расчеты сведены в табл. 1.

ИКС в косоугольной системе координат

Использование такого вида ИКС удобнее, если имеется много лет наблюдений или значения стока велики.

Построения ИКС в косоугольной системе координат выполнены на рис. 2.

2.  Построение гистограммы и статистической кривой обеспеченности максимальных годовых расходов реки Сок.

Гистограмма – ступенчатый график, показывающий вероятность попадания случайной величины в заданный интервал.

Вероятность – количественная оценка возможности появления данного случайного события.

Событие – любой факт, который может реализоваться или не реализоваться.

Обеспеченность – вероятность попадания случайной величины большей или равной заданной.

Статистическая кривая обеспеченности – суммарный ступенчатый график, показывающий вероятность появления величины, равной или превышающей заданную.

Методы теории вероятности используются в гидрологии для получения математических кривых, позволяющих продлить число лет наблюдений.

Данные для построения гистограммы, кривой сглаживания  и  кривой  обеспеченности   приведены в табл. 2.

Гистограмма изображена на рис. 3.

3.  Построение математической и эмпирической кривых обеспеченности максимальных годовых расходов реки Сок.

Дисперсия D характеризует меру рассеяния случайной величины относительно ее математического ожидания.

Среднеквадратическое отклонение (данные взяты из табл. 3):

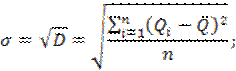
Коэффициент вариации Cv характеризует меру рассеяния плотности вероятности:

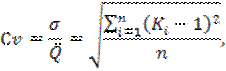
где  Ki – модульный коэффициент,

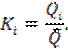
C_v = √(2,6810/25) = 0,33.

При увеличении Сv кривая распределения плотности вероятности растягивается вдоль оси ординат, а кривая обеспеченности поворачивается по часовой стрелке.

Коэффициент асимметрии Сs:

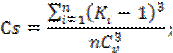
C_s = 0,5757/(0,33³* 25) = 0,66

При увеличении коэффициента асимметрии концы кривой обеспеченности идут более круто, а средняя часть опускается параллельно оси абсцисс.

Подобным кривым соответствует кривая интеграла Пирсена 3-го рода:

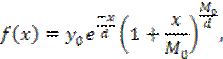
где Мо – мода – точка на кривой распределения плотности вероятности, соответствующая максимальному числу появлений случайной величины;

d – радиус асимметрии;

у0 – значение вероятности при моде (модальная вероятность).

Исходя из соотношения Cs и Cv по двухпараметрическим таблицам [1] строится математическая кривая (рис. 4).

В математической статистике и теории вероятности говорят не о самих коэффициентах Cs и Cv, а об их оценке. Такие оценки называют смещенными, а смещение обусловлено малым сроком лет наблюдений и наличием связи между членами ряда.

Существуют способы определения несмещенных параметров:

Метод моментов

Коэффициент автокорреляции r(1) показывает связь между величинами (значения для расчета r(1) сведены в табл. 4):

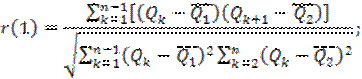
r(1) = 0,554

Коэффициенты a и b:

a₁=0; a₂=1,75; a₃=1,00; a₄=-1,79; a₅=-0,05; a₆=21,13;

b₁=0,03; b₂=1,63; b₃=0,92; b₄=-0,97; b₅=0,03; b₆=7,94.

C_v = 0,07 + 0,9284*0,33 + 0,7952*0,33² = 0,46

C_s = 0,0952 + 0,8812*0,66 + 0,3476*0,66² = 0,82

По двухпараметрическим таблицам исходя из значений Сv и Cs строится кривая, отвечающая методу моментов (рис.4).

Метод наибольшего правдоподобия

Данные для вычислений сведены в табл. 3.

По номограмме кривой трехпараметрического гамма-распределения для Cv=0,4-0,7 получаем:

Cs=3Cv;

Cv=0,61;

Cs=3,66.

По двухпараметрическим таблицам исходя из значений Сv и Cs строится кривая, отвечающая методу наибольшего правдоподобия (рис.4).

4.  Вычисление коэффициента корреляции между максимальными наблюденными расходами рек Сок  и Черемшан и удлинение ряда наблюдений

Река Черемшан – изучаемая река, Сок – река-аналог.

Вычисление коэффициента корреляции (данные для вычисления сведены в табл. 5).

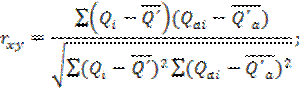
r_xy = 1704420,5/√(681912,10*4385092,5) = 0,99

Для пользования методом наименьших квадратов необходимо выполнение следующих условий:

1)  .

Это условие выполняется.

2)

а₂ – коэффициент регрессии;

σ_а2 – среднеквадратическое отклонение.

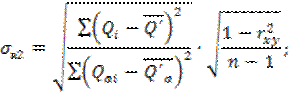
σ_а2 = 0,0112

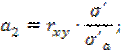
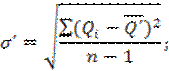
σ' = 168,56;

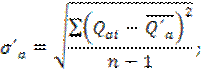
σ'_a = 427,44;

a₂ = 0,3904

a₂/ σ_а2 = 0,3904/0,0112 = 34,85 > 2

Условие выполняется.

Уравнение прямой регрессии:

a₁ – свободный член.

По полученному уравнению можно продлить ряд лет наблюдений изучаемой реки (см. табл. 6).

5.  Определение максимальных расчетных расходов для реки Сок при условии строительства гидротехнического сооружения I класса капитальности

Для II-го класса капитальности при работе сооружения в нормальных условиях вероятность максимальных расходов p=0,1%.

Коэффициент запаса для поверочного  расхода K_max= 3,04, тогда

Q_max = K_max * Q = 3,04 * 1829,4 = 5561,37 м³/с

При работе в чрезвычайных условиях вероятность максимальных расходов р=0,1%. К_max=2,16, тогда

Q_max = K_max * Q = 2,16 * 1829,4 = 3951,5 м³/с 
Список литературы

1)  Канарский Н.Д., Михалев М.А. Гидрологические расчеты. Учебное пособие. – ЛПИ, 1984. – 64 с.